A Unified Approach to Count-Based Weakly-Supervised Learning

High-quality labels are often very scarce, whereas unlabeled data with inferred weak labels occurs more naturally. In many cases, these weak labels dictate the frequency of each respective class over a set of instances. In this paper, we develop a unified approach to learning from such weakly-labeled data, which we call count-based weakly-supervised learning. At the heart of our approach is the ability to compute the probability of exactly k out of n outputs being set to true. This computation is differentiable, exact, and efficient. Building upon the previous computation, we derive a count loss penalizing the model for deviations in its distribution from an arithmetic constraint defined over label counts. We evaluate our approach on three common weakly-supervised learning paradigms and observe that our proposed approach achieves state-of-the-art or highly competitive results across all three of the paradigms.

Probabilistically Rewired Message-Passing Neural Networks

Message-passing graph neural networks (MPNNs) emerged as powerful tools for processing graph-structured input. However, they operate on a fixed input graph structure, ignoring potential noise and missing information. Furthermore, their local aggregation mechanism can lead to problems such as over-squashing and limited expressive power in capturing relevant graph structures. Existing solutions to these challenges have primarily relied on heuristic methods, often disregarding the underlying data distribution. Hence, devising principled approaches for learning to infer graph structures relevant to the given prediction task remains an open challenge. In this work, leveraging recent progress in exact and differentiable $k$-subset sampling, we devise probabilistically rewired MPNNs (PR-MPNNs), which learn to add relevant edges while omitting less beneficial ones. For the first time, our theoretical analysis explores how PR-MPNNs enhance expressive power, and we identify precise conditions under which they outperform purely randomized approaches. Empirically, we demonstrate that our approach effectively mitigates issues like over-squashing and under-reaching. In addition, on established real-world datasets, our method exhibits competitive or superior predictive performance compared to traditional MPNN models and recent graph transformer architectures.

Collapsed Inference for Bayesian Deep Learning

Bayesian neural networks (BNNs) provide a formalism to quantify and calibrate uncertainty in deep learning. Current inference approaches for BNNs often resort to few-sample estimation for scalability, which can harm predictive performance, while its alternatives tend to be computationally prohibitively expensive. We tackle this challenge by revealing a previously unseen connection between inference on BNNs and volume computation problems. With this observation, we introduce a novel collapsed inference scheme that performs Bayesian model averaging using collapsed samples. It improves over a Monte-Carlo sample by limiting sampling to a subset of the network weights while pairing it with some closed-form conditional distribution over the rest. A collapsed sample represents uncountably many models drawn from the approximate posterior and thus yields higher sample efficiency. Further, we show that the marginalization of a collapsed sample can be solved analytically and efficiently despite the non-linearity of neural networks by leveraging existing volume computation solvers. Our proposed use of collapsed samples achieves a balance between scalability and accuracy. On various regression and classification tasks, our collapsed Bayesian deep learning approach demonstrates significant improvements over existing methods and sets a new state of the art in terms of uncertainty estimation as well as predictive performance.

SIMPLE: A Gradient Estimator for $k$-Subset Sampling

$k$-subset sampling is ubiquitous in machine learning, enabling regularization and interpretability through sparsity. The challenge lies in rendering $k$-subset sampling amenable to end-to-end learning. This has typically involved relaxing the reparameterized samples to allow for backpropagation, with the risk of introducing high bias and high variance. In this work, we fall back to discrete $k$-subset sampling on the forward pass. This is coupled with using the gradient with respect to the exact marginals, computed efficiently, as a proxy for the true gradient. We show that our gradient estimator, SIMPLE, exhibits lower bias and variance compared to state-of-the-art estimators, including the straight-through Gumbel estimator when $k = 1$. Empirical results show improved performance on learning to explain and sparse linear regression. We provide an algorithm for computing the exact ELBO for the $k$-subset distribution, obtaining significantly lower loss compared to SOTA.

Tractable Computation of Expected Kernels by Circuits

Computing the expectation of some kernel function is ubiquitous in machine learning, from the classical theory of support vector machines, to exploiting kernel embeddings of distributions in applications ranging from probabilistic modeling, statistical inference, casual discovery, and deep learning. In all these scenarios, we tend to resort to Monte Carlo estimates as expectations of kernels are intractable in general. In this work, we characterize the conditions under which we can compute expected kernels exactly and efficiently, by leveraging recent advances in probabilistic circuit representations. We first construct a circuit representation for kernels and propose an approach to such tractable computation. We then demonstrate possible advancements for kernel embedding frameworks by exploiting tractable expected kernels to derive new algorithms for two challenging scenarios: 1) reasoning under missing data with kernel support vector regressors; 2) devising a collapsed black-box importance sampling scheme. Finally, we empirically evaluate both algorithms and show that they outperform standard baselines on a variety of datasets.

Scaling up Hybrid Probabilistic Inference with Logical and Arithmetic Constraints via Message Passing

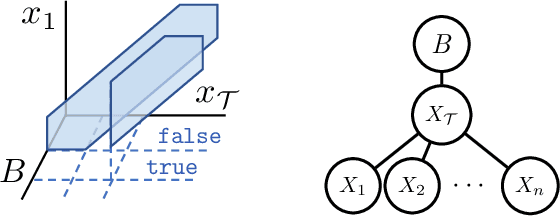
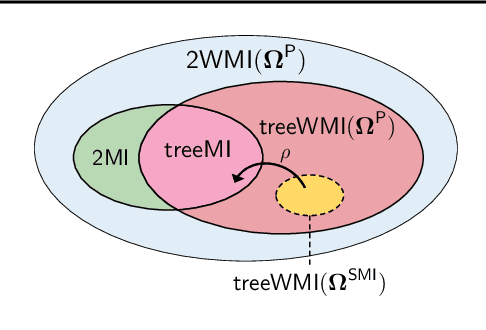
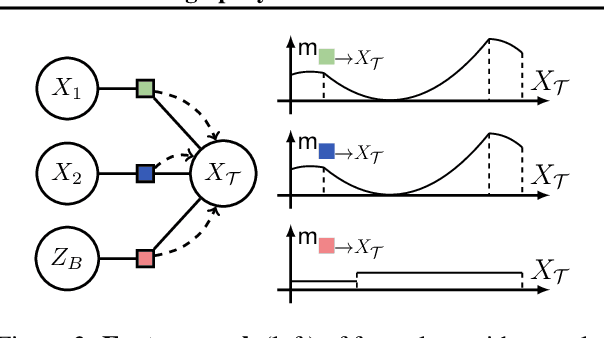
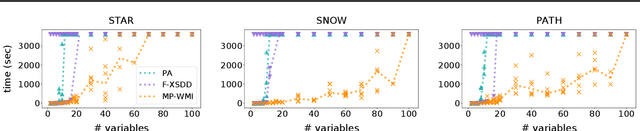
Weighted model integration (WMI) is a very appealing framework for probabilistic inference: it allows to express the complex dependencies of real-world problems where variables are both continuous and discrete, via the language of Satisfiability Modulo Theories (SMT), as well as to compute probabilistic queries with complex logical and arithmetic constraints. Yet, existing WMI solvers are not ready to scale to these problems. They either ignore the intrinsic dependency structure of the problem at all, or they are limited to too restrictive structures. To narrow this gap, we derive a factorized formalism of WMI enabling us to devise a scalable WMI solver based on message passing, MP-WMI. Namely, MP-WMI is the first WMI solver which allows to: 1) perform exact inference on the full class of tree-structured WMI problems; 2) compute all marginal densities in linear time; 3) amortize inference inter query. Experimental results show that our solver dramatically outperforms the existing WMI solvers on a large set of benchmarks.

Hybrid Probabilistic Inference with Logical Constraints: Tractability and Message Passing

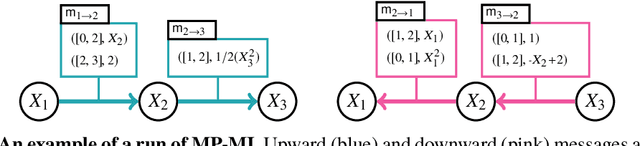
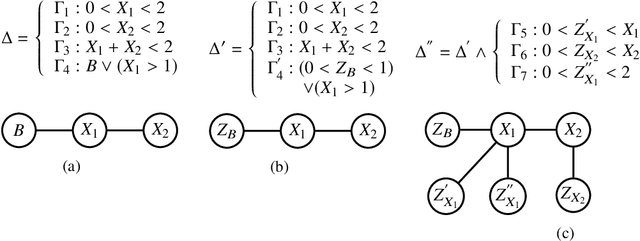
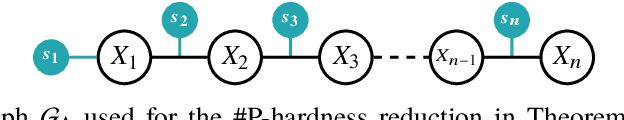
Weighted model integration (WMI) is a very appealing framework for probabilistic inference: it allows to express the complex dependencies of real-world hybrid scenarios where variables are heterogeneous in nature (both continuous and discrete) via the language of Satisfiability Modulo Theories (SMT); as well as computing probabilistic queries with arbitrarily complex logical constraints. Recent work has shown WMI inference to be reducible to a model integration (MI) problem, under some assumptions, thus effectively allowing hybrid probabilistic reasoning by volume computations. In this paper, we introduce a novel formulation of MI via a message passing scheme that allows to efficiently compute the marginal densities and statistical moments of all the variables in linear time. As such, we are able to amortize inference for arbitrarily rich MI queries when they conform to the problem structure, here represented as the primal graph associated to the SMT formula. Furthermore, we theoretically trace the tractability boundaries of exact MI. Indeed, we prove that in terms of the structural requirements on the primal graph that make our MI algorithm tractable - bounding its diameter and treewidth - the bounds are not only sufficient, but necessary for tractable inference via MI.

Efficient Search-Based Weighted Model Integration

Weighted model integration (WMI) extends Weighted model counting (WMC) to the integration of functions over mixed discrete-continuous domains. It has shown tremendous promise for solving inference problems in graphical models and probabilistic programming. Yet, state-of-the-art tools for WMI are limited in terms of performance and ignore the independence structure that is crucial to improving efficiency. To address this limitation, we propose an efficient model integration algorithm for theories with tree primal graphs. We exploit the sparse graph structure by using search to performing integration. Our algorithm greatly improves the computational efficiency on such problems and exploits context-specific independence between variables. Experimental results show dramatic speedups compared to existing WMI solvers on problems with tree-shaped dependencies.

Stein Variational Message Passing for Continuous Graphical Models

We propose a novel distributed inference algorithm for continuous graphical models, by extending Stein variational gradient descent (SVGD) to leverage the Markov dependency structure of the distribution of interest. Our approach combines SVGD with a set of structured local kernel functions defined on the Markov blanket of each node, which alleviates the curse of high dimensionality and simultaneously yields a distributed algorithm for decentralized inference tasks. We justify our method with theoretical analysis and show that the use of local kernels can be viewed as a new type of localized approximation that matches the target distribution on the conditional distributions of each node over its Markov blanket. Our empirical results show that our method outperforms a variety of baselines including standard MCMC and particle message passing methods.