GraIP: A Benchmarking Framework For Neural Graph Inverse Problems

A wide range of graph learning tasks, such as structure discovery, temporal graph analysis, and combinatorial optimization, focus on inferring graph structures from data, rather than making predictions on given graphs. However, the respective methods to solve such problems are often developed in an isolated, task-specific manner and thus lack a unifying theoretical foundation. Here, we provide a stepping stone towards the formation of such a foundation and further development by introducing the Neural Graph Inverse Problem (GraIP) conceptual framework, which formalizes and reframes a broad class of graph learning tasks as inverse problems. Unlike discriminative approaches that directly predict target variables from given graph inputs, the GraIP paradigm addresses inverse problems, i.e., it relies on observational data and aims to recover the underlying graph structure by reversing the forward process, such as message passing or network dynamics, that produced the observed outputs. We demonstrate the versatility of GraIP across various graph learning tasks, including rewiring, causal discovery, and neural relational inference. We also propose benchmark datasets and metrics for each GraIP domain considered, and characterize and empirically evaluate existing baseline methods used to solve them. Overall, our unifying perspective bridges seemingly disparate applications and provides a principled approach to structural learning in constrained and combinatorial settings while encouraging cross-pollination of existing methods across graph inverse problems.

Principled Latent Diffusion for Graphs via Laplacian Autoencoders

Graph diffusion models achieve state-of-the-art performance in graph generation but suffer from quadratic complexity in the number of nodes -- and much of their capacity is wasted modeling the absence of edges in sparse graphs. Inspired by latent diffusion in other modalities, a natural idea is to compress graphs into a low-dimensional latent space and perform diffusion there. However, unlike images or text, graph generation requires nearly lossless reconstruction, as even a single error in decoding an adjacency matrix can render the entire sample invalid. This challenge has remained largely unaddressed. We propose LG-Flow, a latent graph diffusion framework that directly overcomes these obstacles. A permutation-equivariant autoencoder maps each node into a fixed-dimensional embedding from which the full adjacency is provably recoverable, enabling near-lossless reconstruction for both undirected graphs and DAGs. The dimensionality of this latent representation scales linearly with the number of nodes, eliminating the quadratic bottleneck and making it feasible to train larger and more expressive models. In this latent space, we train a Diffusion Transformer with flow matching, enabling efficient and expressive graph generation. Our approach achieves competitive results against state-of-the-art graph diffusion models, while achieving up to $1000\times$ speed-up.

Generalizable Insights for Graph Transformers in Theory and Practice

Graph Transformers (GTs) have shown strong empirical performance, yet current architectures vary widely in their use of attention mechanisms, positional embeddings (PEs), and expressivity. Existing expressivity results are often tied to specific design choices and lack comprehensive empirical validation on large-scale data. This leaves a gap between theory and practice, preventing generalizable insights that exceed particular application domains. Here, we propose the Generalized-Distance Transformer (GDT), a GT architecture using standard attention that incorporates many advancements for GTs from recent years, and develop a fine-grained understanding of the GDT's representation power in terms of attention and PEs. Through extensive experiments, we identify design choices that consistently perform well across various applications, tasks, and model scales, demonstrating strong performance in a few-shot transfer setting without fine-tuning. Our evaluation covers over eight million graphs with roughly 270M tokens across diverse domains, including image-based object detection, molecular property prediction, code summarization, and out-of-distribution algorithmic reasoning. We distill our theoretical and practical findings into several generalizable insights about effective GT design, training, and inference.

Understanding Generalization in Node and Link Prediction

Using message-passing graph neural networks (MPNNs) for node and link prediction is crucial in various scientific and industrial domains, which has led to the development of diverse MPNN architectures. Besides working well in practical settings, their ability to generalize beyond the training set remains poorly understood. While some studies have explored MPNNs' generalization in graph-level prediction tasks, much less attention has been given to node- and link-level predictions. Existing works often rely on unrealistic i.i.d.\@ assumptions, overlooking possible correlations between nodes or links, and assuming fixed aggregation and impractical loss functions while neglecting the influence of graph structure. In this work, we introduce a unified framework to analyze the generalization properties of MPNNs in inductive and transductive node and link prediction settings, incorporating diverse architectural parameters and loss functions and quantifying the influence of graph structure. Additionally, our proposed generalization framework can be applied beyond graphs to any classification task under the inductive or transductive setting. Our empirical study supports our theoretical insights, deepening our understanding of MPNNs' generalization capabilities in these tasks.

Survey on Generalization Theory for Graph Neural Networks

Message-passing graph neural networks (MPNNs) have emerged as the leading approach for machine learning on graphs, attracting significant attention in recent years. While a large set of works explored the expressivity of MPNNs, i.e., their ability to separate graphs and approximate functions over them, comparatively less attention has been directed toward investigating their generalization abilities, i.e., making meaningful predictions beyond the training data. Here, we systematically review the existing literature on the generalization abilities of MPNNs. We analyze the strengths and limitations of various studies in these domains, providing insights into their methodologies and findings. Furthermore, we identify potential avenues for future research, aiming to deepen our understanding of the generalization abilities of MPNNs.

Position: Graph Learning Will Lose Relevance Due To Poor Benchmarks

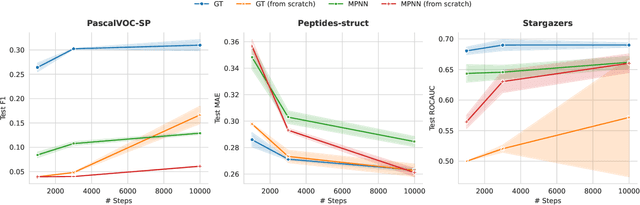
While machine learning on graphs has demonstrated promise in drug design and molecular property prediction, significant benchmarking challenges hinder its further progress and relevance. Current benchmarking practices often lack focus on transformative, real-world applications, favoring narrow domains like two-dimensional molecular graphs over broader, impactful areas such as combinatorial optimization, relational databases, or chip design. Additionally, many benchmark datasets poorly represent the underlying data, leading to inadequate abstractions and misaligned use cases. Fragmented evaluations and an excessive focus on accuracy further exacerbate these issues, incentivizing overfitting rather than fostering generalizable insights. These limitations have prevented the development of truly useful graph foundation models. This position paper calls for a paradigm shift toward more meaningful benchmarks, rigorous evaluation protocols, and stronger collaboration with domain experts to drive impactful and reliable advances in graph learning research, unlocking the potential of graph learning.

Towards graph neural networks for provably solving convex optimization problems

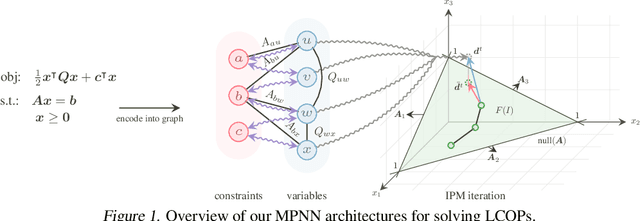
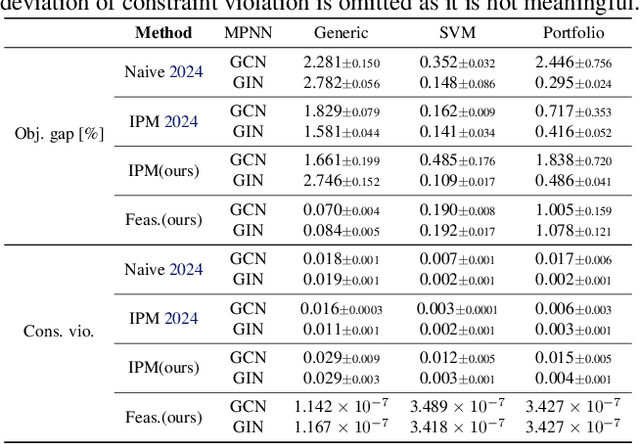
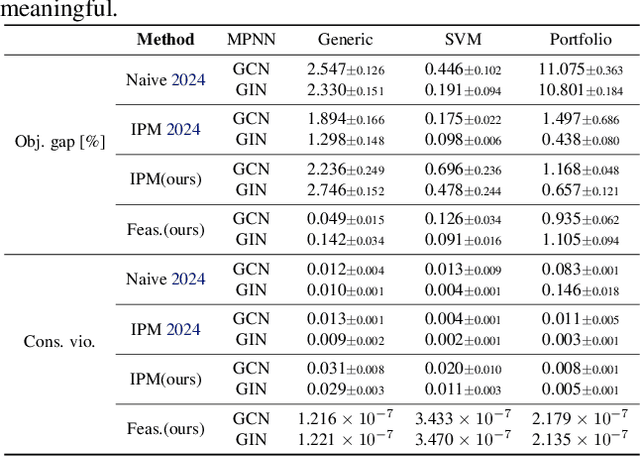
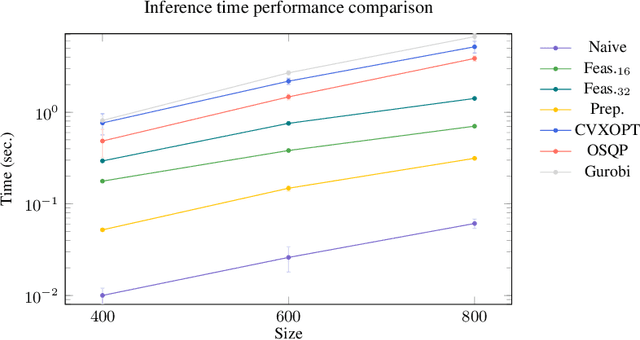
Recently, message-passing graph neural networks (MPNNs) have shown potential for solving combinatorial and continuous optimization problems due to their ability to capture variable-constraint interactions. While existing approaches leverage MPNNs to approximate solutions or warm-start traditional solvers, they often lack guarantees for feasibility, particularly in convex optimization settings. Here, we propose an iterative MPNN framework to solve convex optimization problems with provable feasibility guarantees. First, we demonstrate that MPNNs can provably simulate standard interior-point methods for solving quadratic problems with linear constraints, covering relevant problems such as SVMs. Secondly, to ensure feasibility, we introduce a variant that starts from a feasible point and iteratively restricts the search within the feasible region. Experimental results show that our approach outperforms existing neural baselines in solution quality and feasibility, generalizes well to unseen problem sizes, and, in some cases, achieves faster solution times than state-of-the-art solvers such as Gurobi.

Covered Forest: Fine-grained generalization analysis of graph neural networks

The expressive power of message-passing graph neural networks (MPNNs) is reasonably well understood, primarily through combinatorial techniques from graph isomorphism testing. However, MPNNs' generalization abilities -- making meaningful predictions beyond the training set -- remain less explored. Current generalization analyses often overlook graph structure, limit the focus to specific aggregation functions, and assume the impractical, hard-to-optimize $0$-$1$ loss function. Here, we extend recent advances in graph similarity theory to assess the influence of graph structure, aggregation, and loss functions on MPNNs' generalization abilities. Our empirical study supports our theoretical insights, improving our understanding of MPNNs' generalization properties.

Cometh: A continuous-time discrete-state graph diffusion model

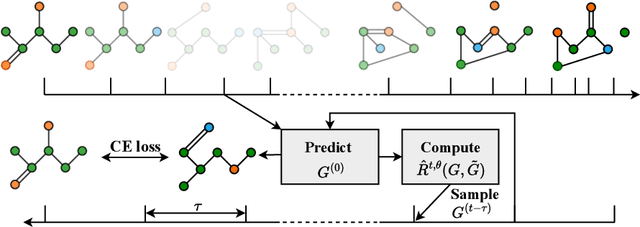
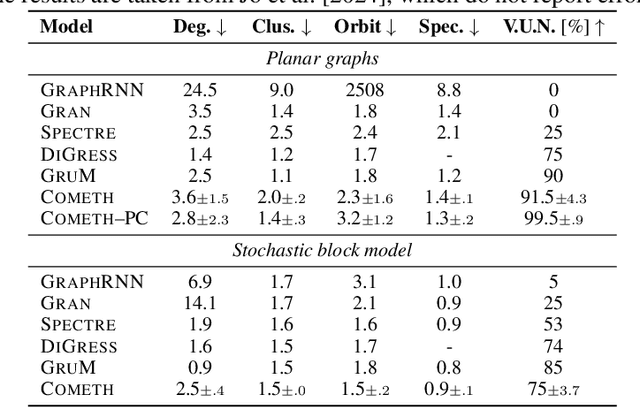
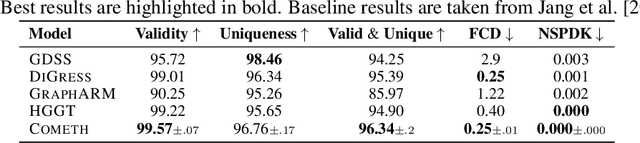
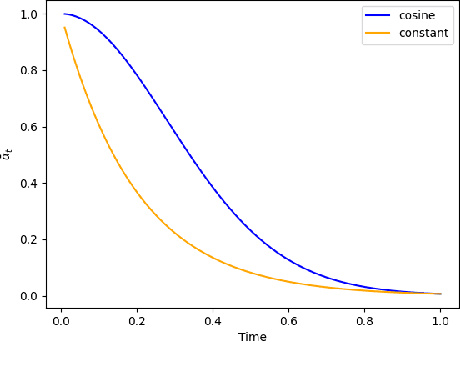
Discrete-state denoising diffusion models led to state-of-the-art performance in graph generation, especially in the molecular domain. Recently, they have been transposed to continuous time, allowing more flexibility in the reverse process and a better trade-off between sampling efficiency and quality. Here, to leverage the benefits of both approaches, we propose Cometh, a continuous-time discrete-state graph diffusion model, integrating graph data into a continuous-time diffusion model framework. Empirically, we show that integrating continuous time leads to significant improvements across various metrics over state-of-the-art discrete-state diffusion models on a large set of molecular and non-molecular benchmark datasets.

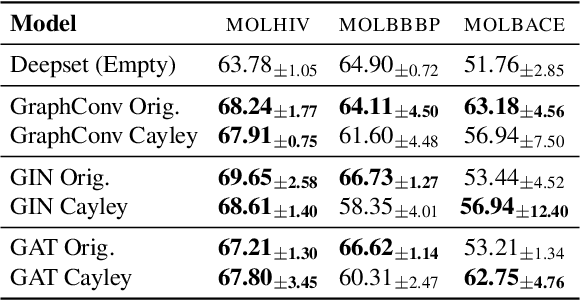
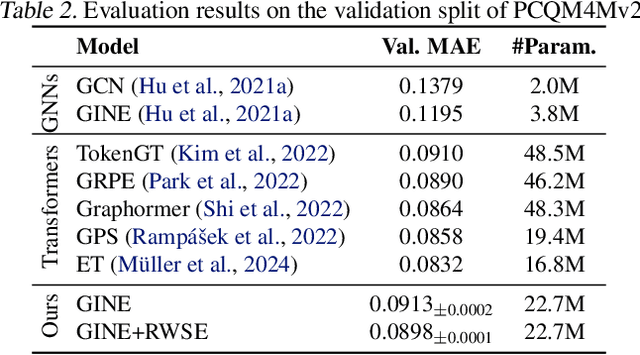
Aligning Transformers with Weisfeiler-Leman

Graph neural network architectures aligned with the $k$-dimensional Weisfeiler--Leman ($k$-WL) hierarchy offer theoretically well-understood expressive power. However, these architectures often fail to deliver state-of-the-art predictive performance on real-world graphs, limiting their practical utility. While recent works aligning graph transformer architectures with the $k$-WL hierarchy have shown promising empirical results, employing transformers for higher orders of $k$ remains challenging due to a prohibitive runtime and memory complexity of self-attention as well as impractical architectural assumptions, such as an infeasible number of attention heads. Here, we advance the alignment of transformers with the $k$-WL hierarchy, showing stronger expressivity results for each $k$, making them more feasible in practice. In addition, we develop a theoretical framework that allows the study of established positional encodings such as Laplacian PEs and SPE. We evaluate our transformers on the large-scale PCQM4Mv2 dataset, showing competitive predictive performance with the state-of-the-art and demonstrating strong downstream performance when fine-tuning them on small-scale molecular datasets. Our code is available at https://github.com/luis-mueller/wl-transformers.