Covered Forest: Fine-grained generalization analysis of graph neural networks

The expressive power of message-passing graph neural networks (MPNNs) is reasonably well understood, primarily through combinatorial techniques from graph isomorphism testing. However, MPNNs' generalization abilities -- making meaningful predictions beyond the training set -- remain less explored. Current generalization analyses often overlook graph structure, limit the focus to specific aggregation functions, and assume the impractical, hard-to-optimize $0$-$1$ loss function. Here, we extend recent advances in graph similarity theory to assess the influence of graph structure, aggregation, and loss functions on MPNNs' generalization abilities. Our empirical study supports our theoretical insights, improving our understanding of MPNNs' generalization properties.

Generalization, Expressivity, and Universality of Graph Neural Networks on Attributed Graphs

We analyze the universality and generalization of graph neural networks (GNNs) on attributed graphs, i.e., with node attributes. To this end, we propose pseudometrics over the space of all attributed graphs that describe the fine-grained expressivity of GNNs. Namely, GNNs are both Lipschitz continuous with respect to our pseudometrics and can separate attributed graphs that are distant in the metric. Moreover, we prove that the space of all attributed graphs is relatively compact with respect to our metrics. Based on these properties, we prove a universal approximation theorem for GNNs and generalization bounds for GNNs on any data distribution of attributed graphs. The proposed metrics compute the similarity between the structures of attributed graphs via a hierarchical optimal transport between computation trees. Our work extends and unites previous approaches which either derived theory only for graphs with no attributes, derived compact metrics under which GNNs are continuous but without separation power, or derived metrics under which GNNs are continuous and separate points but the space of graphs is not relatively compact, which prevents universal approximation and generalization analysis.

PieClam: A Universal Graph Autoencoder Based on Overlapping Inclusive and Exclusive Communities

We propose PieClam (Prior Inclusive Exclusive Cluster Affiliation Model): a probabilistic graph model for representing any graph as overlapping generalized communities. Our method can be interpreted as a graph autoencoder: nodes are embedded into a code space by an algorithm that maximizes the log-likelihood of the decoded graph, given the input graph. PieClam is a community affiliation model that extends well-known methods like BigClam in two main manners. First, instead of the decoder being defined via pairwise interactions between the nodes in the code space, we also incorporate a learned prior on the distribution of nodes in the code space, turning our method into a graph generative model. Secondly, we generalize the notion of communities by allowing not only sets of nodes with strong connectivity, which we call inclusive communities, but also sets of nodes with strong disconnection, which we call exclusive communities. To model both types of communities, we propose a new type of decoder based the Lorentz inner product, which we prove to be much more expressive than standard decoders based on standard inner products or norm distances. By introducing a new graph similarity measure, that we call the log cut distance, we show that PieClam is a universal autoencoder, able to uniformly approximately reconstruct any graph. Our method is shown to obtain competitive performance in graph anomaly detection benchmarks.

Equivariant Machine Learning on Graphs with Nonlinear Spectral Filters

Equivariant machine learning is an approach for designing deep learning models that respect the symmetries of the problem, with the aim of reducing model complexity and improving generalization. In this paper, we focus on an extension of shift equivariance, which is the basis of convolution networks on images, to general graphs. Unlike images, graphs do not have a natural notion of domain translation. Therefore, we consider the graph functional shifts as the symmetry group: the unitary operators that commute with the graph shift operator. Notably, such symmetries operate in the signal space rather than directly in the spatial space. We remark that each linear filter layer of a standard spectral graph neural network (GNN) commutes with graph functional shifts, but the activation function breaks this symmetry. Instead, we propose nonlinear spectral filters (NLSFs) that are fully equivariant to graph functional shifts and show that they have universal approximation properties. The proposed NLSFs are based on a new form of spectral domain that is transferable between graphs. We demonstrate the superior performance of NLSFs over existing spectral GNNs in node and graph classification benchmarks.

Learning on Large Graphs using Intersecting Communities

Message Passing Neural Networks (MPNNs) are a staple of graph machine learning. MPNNs iteratively update each node's representation in an input graph by aggregating messages from the node's neighbors, which necessitates a memory complexity of the order of the number of graph edges. This complexity might quickly become prohibitive for large graphs provided they are not very sparse. In this paper, we propose a novel approach to alleviate this problem by approximating the input graph as an intersecting community graph (ICG) -- a combination of intersecting cliques. The key insight is that the number of communities required to approximate a graph does not depend on the graph size. We develop a new constructive version of the Weak Graph Regularity Lemma to efficiently construct an approximating ICG for any input graph. We then devise an efficient graph learning algorithm operating directly on ICG in linear memory and time with respect to the number of nodes (rather than edges). This offers a new and fundamentally different pipeline for learning on very large non-sparse graphs, whose applicability is demonstrated empirically on node classification tasks and spatio-temporal data processing.

Generalization Bounds for Message Passing Networks on Mixture of Graphons

We study the generalization capabilities of Message Passing Neural Networks (MPNNs), a prevalent class of Graph Neural Networks (GNN). We derive generalization bounds specifically for MPNNs with normalized sum aggregation and mean aggregation. Our analysis is based on a data generation model incorporating a finite set of template graphons. Each graph within this framework is generated by sampling from one of the graphons with a certain degree of perturbation. In particular, we extend previous MPNN generalization results to a more realistic setting, which includes the following modifications: 1) we analyze simple random graphs with Bernoulli-distributed edges instead of weighted graphs; 2) we sample both graphs and graph signals from perturbed graphons instead of clean graphons; and 3) we analyze sparse graphs instead of dense graphs. In this more realistic and challenging scenario, we provide a generalization bound that decreases as the average number of nodes in the graphs increases. Our results imply that MPNNs with higher complexity than the size of the training set can still generalize effectively, as long as the graphs are sufficiently large.

Future Directions in Foundations of Graph Machine Learning

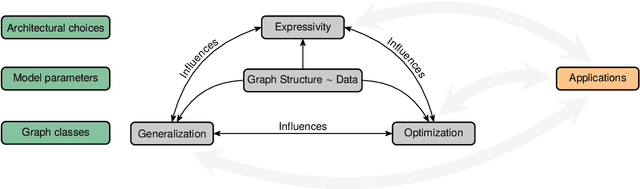
Machine learning on graphs, especially using graph neural networks (GNNs), has seen a surge in interest due to the wide availability of graph data across a broad spectrum of disciplines, from life to social and engineering sciences. Despite their practical success, our theoretical understanding of the properties of GNNs remains highly incomplete. Recent theoretical advancements primarily focus on elucidating the coarse-grained expressive power of GNNs, predominantly employing combinatorial techniques. However, these studies do not perfectly align with practice, particularly in understanding the generalization behavior of GNNs when trained with stochastic first-order optimization techniques. In this position paper, we argue that the graph machine learning community needs to shift its attention to developing a more balanced theory of graph machine learning, focusing on a more thorough understanding of the interplay of expressive power, generalization, and optimization.

The First Pathloss Radio Map Prediction Challenge

To foster research and facilitate fair comparisons among recently proposed pathloss radio map prediction methods, we have launched the ICASSP 2023 First Pathloss Radio Map Prediction Challenge. In this short overview paper, we briefly describe the pathloss prediction problem, the provided datasets, the challenge task and the challenge evaluation methodology. Finally, we present the results of the challenge.

Approximately Equivariant Graph Networks

Graph neural networks (GNNs) are commonly described as being permutation equivariant with respect to node relabeling in the graph. This symmetry of GNNs is often compared to the translation equivariance symmetry of Euclidean convolution neural networks (CNNs). However, these two symmetries are fundamentally different: The translation equivariance of CNNs corresponds to symmetries of the fixed domain acting on the image signal (sometimes known as active symmetries), whereas in GNNs any permutation acts on both the graph signals and the graph domain (sometimes described as passive symmetries). In this work, we focus on the active symmetries of GNNs, by considering a learning setting where signals are supported on a fixed graph. In this case, the natural symmetries of GNNs are the automorphisms of the graph. Since real-world graphs tend to be asymmetric, we relax the notion of symmetries by formalizing approximate symmetries via graph coarsening. We present a bias-variance formula that quantifies the tradeoff between the loss in expressivity and the gain in the regularity of the learned estimator, depending on the chosen symmetry group. To illustrate our approach, we conduct extensive experiments on image inpainting, traffic flow prediction, and human pose estimation with different choices of symmetries. We show theoretically and empirically that the best generalization performance can be achieved by choosing a suitably larger group than the graph automorphism group, but smaller than the full permutation group.

Fine-grained Expressivity of Graph Neural Networks

Numerous recent works have analyzed the expressive power of message-passing graph neural networks (MPNNs), primarily utilizing combinatorial techniques such as the $1$-dimensional Weisfeiler-Leman test ($1$-WL) for the graph isomorphism problem. However, the graph isomorphism objective is inherently binary, not giving insights into the degree of similarity between two given graphs. This work resolves this issue by considering continuous extensions of both $1$-WL and MPNNs to graphons. Concretely, we show that the continuous variant of $1$-WL delivers an accurate topological characterization of the expressive power of MPNNs on graphons, revealing which graphs these networks can distinguish and the level of difficulty in separating them. We identify the finest topology where MPNNs separate points and prove a universal approximation theorem. Consequently, we provide a theoretical framework for graph and graphon similarity combining various topological variants of classical characterizations of the $1$-WL. In particular, we characterize the expressive power of MPNNs in terms of the tree distance, which is a graph distance based on the concepts of fractional isomorphisms, and substructure counts via tree homomorphisms, showing that these concepts have the same expressive power as the $1$-WL and MPNNs on graphons. Empirically, we validate our theoretical findings by showing that randomly initialized MPNNs, without training, exhibit competitive performance compared to their trained counterparts. Moreover, we evaluate different MPNN architectures based on their ability to preserve graph distances, highlighting the significance of our continuous $1$-WL test in understanding MPNNs' expressivity.