Coupled Hierarchical Structure Learning using Tree-Wasserstein Distance

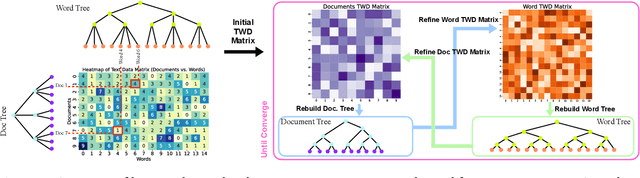
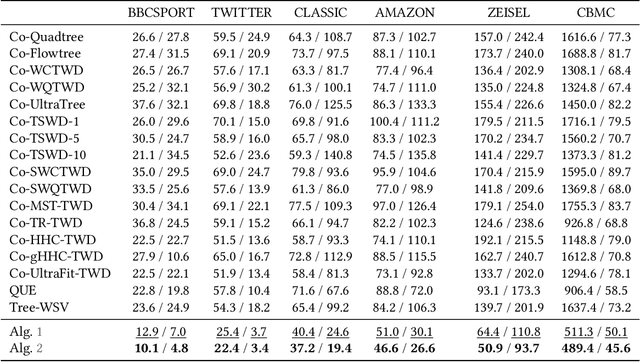
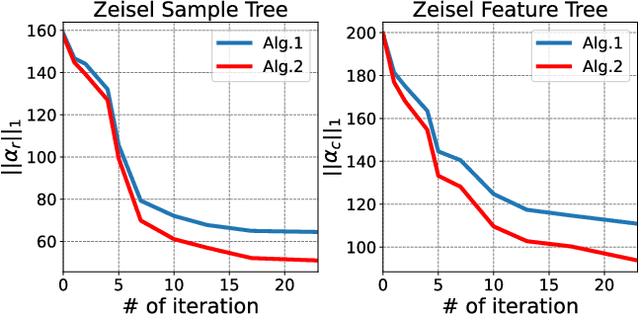
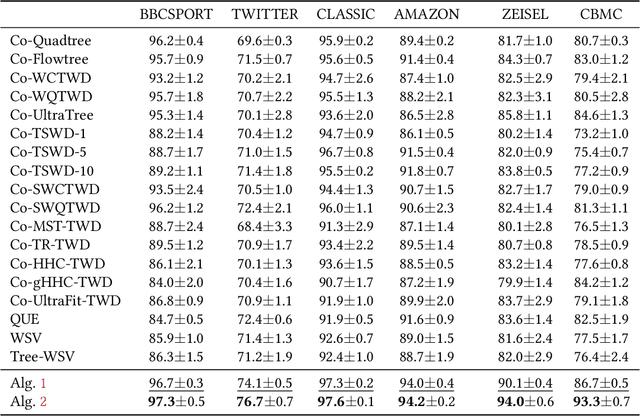
In many applications, both data samples and features have underlying hierarchical structures. However, existing methods for learning these latent structures typically focus on either samples or features, ignoring possible coupling between them. In this paper, we introduce a coupled hierarchical structure learning method using tree-Wasserstein distance (TWD). Our method jointly computes TWDs for samples and features, representing their latent hierarchies as trees. We propose an iterative, unsupervised procedure to build these sample and feature trees based on diffusion geometry, hyperbolic geometry, and wavelet filters. We show that this iterative procedure converges and empirically improves the quality of the constructed trees. The method is also computationally efficient and scales well in high-dimensional settings. Our method can be seamlessly integrated with hyperbolic graph convolutional networks (HGCN). We demonstrate that our method outperforms competing approaches in sparse approximation and unsupervised Wasserstein distance learning on several word-document and single-cell RNA-sequencing datasets. In addition, integrating our method into HGCN enhances performance in link prediction and node classification tasks.

Tree-Wasserstein Distance for High Dimensional Data with a Latent Feature Hierarchy

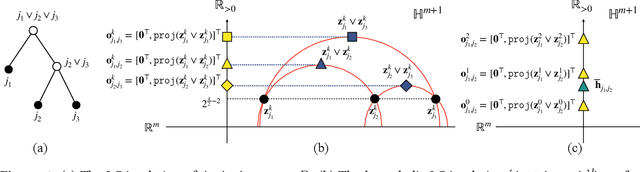
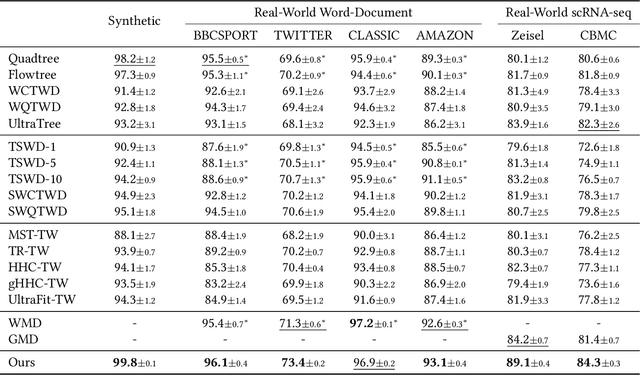
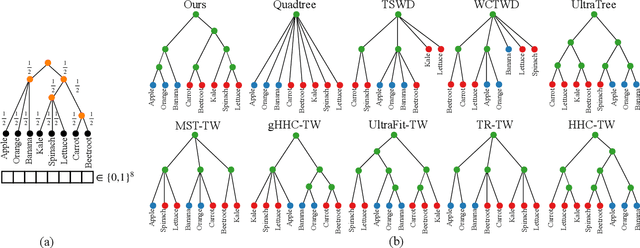
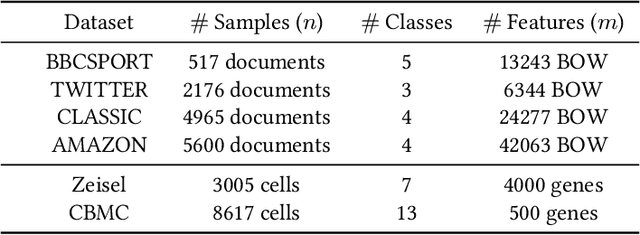
Finding meaningful distances between high-dimensional data samples is an important scientific task. To this end, we propose a new tree-Wasserstein distance (TWD) for high-dimensional data with two key aspects. First, our TWD is specifically designed for data with a latent feature hierarchy, i.e., the features lie in a hierarchical space, in contrast to the usual focus on embedding samples in hyperbolic space. Second, while the conventional use of TWD is to speed up the computation of the Wasserstein distance, we use its inherent tree as a means to learn the latent feature hierarchy. The key idea of our method is to embed the features into a multi-scale hyperbolic space using diffusion geometry and then present a new tree decoding method by establishing analogies between the hyperbolic embedding and trees. We show that our TWD computed based on data observations provably recovers the TWD defined with the latent feature hierarchy and that its computation is efficient and scalable. We showcase the usefulness of the proposed TWD in applications to word-document and single-cell RNA-sequencing datasets, demonstrating its advantages over existing TWDs and methods based on pre-trained models.

Equivariant Machine Learning on Graphs with Nonlinear Spectral Filters

Equivariant machine learning is an approach for designing deep learning models that respect the symmetries of the problem, with the aim of reducing model complexity and improving generalization. In this paper, we focus on an extension of shift equivariance, which is the basis of convolution networks on images, to general graphs. Unlike images, graphs do not have a natural notion of domain translation. Therefore, we consider the graph functional shifts as the symmetry group: the unitary operators that commute with the graph shift operator. Notably, such symmetries operate in the signal space rather than directly in the spatial space. We remark that each linear filter layer of a standard spectral graph neural network (GNN) commutes with graph functional shifts, but the activation function breaks this symmetry. Instead, we propose nonlinear spectral filters (NLSFs) that are fully equivariant to graph functional shifts and show that they have universal approximation properties. The proposed NLSFs are based on a new form of spectral domain that is transferable between graphs. We demonstrate the superior performance of NLSFs over existing spectral GNNs in node and graph classification benchmarks.

Hyperbolic Diffusion Embedding and Distance for Hierarchical Representation Learning

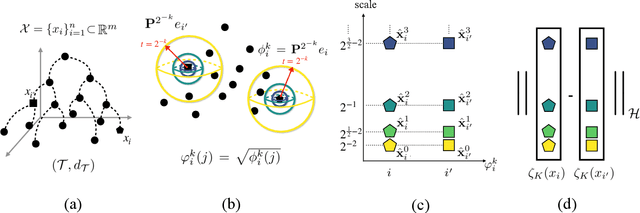
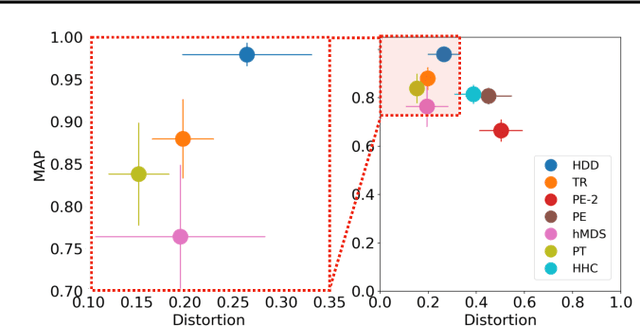
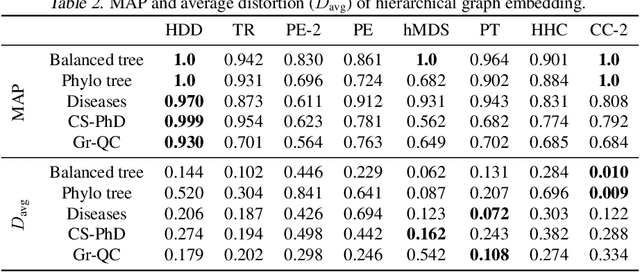
Finding meaningful representations and distances of hierarchical data is important in many fields. This paper presents a new method for hierarchical data embedding and distance. Our method relies on combining diffusion geometry, a central approach to manifold learning, and hyperbolic geometry. Specifically, using diffusion geometry, we build multi-scale densities on the data, aimed to reveal their hierarchical structure, and then embed them into a product of hyperbolic spaces. We show theoretically that our embedding and distance recover the underlying hierarchical structure. In addition, we demonstrate the efficacy of the proposed method and its advantages compared to existing methods on graph embedding benchmarks and hierarchical datasets.