Unsupervised Feature Selection Through Group Discovery

Unsupervised feature selection (FS) is essential for high-dimensional learning tasks where labels are not available. It helps reduce noise, improve generalization, and enhance interpretability. However, most existing unsupervised FS methods evaluate features in isolation, even though informative signals often emerge from groups of related features. For example, adjacent pixels, functionally connected brain regions, or correlated financial indicators tend to act together, making independent evaluation suboptimal. Although some methods attempt to capture group structure, they typically rely on predefined partitions or label supervision, limiting their applicability. We propose GroupFS, an end-to-end, fully differentiable framework that jointly discovers latent feature groups and selects the most informative groups among them, without relying on fixed a priori groups or label supervision. GroupFS enforces Laplacian smoothness on both feature and sample graphs and applies a group sparsity regularizer to learn a compact, structured representation. Across nine benchmarks spanning images, tabular data, and biological datasets, GroupFS consistently outperforms state-of-the-art unsupervised FS in clustering and selects groups of features that align with meaningful patterns.

Robust Tangent Space Estimation via Laplacian Eigenvector Gradient Orthogonalization

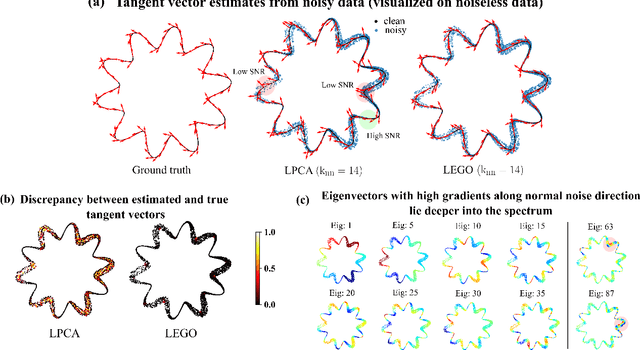
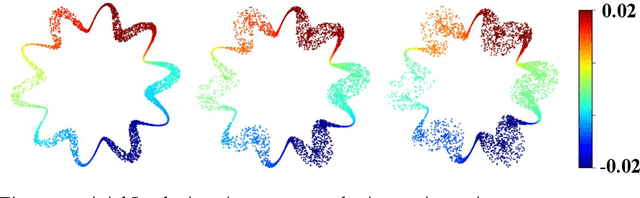
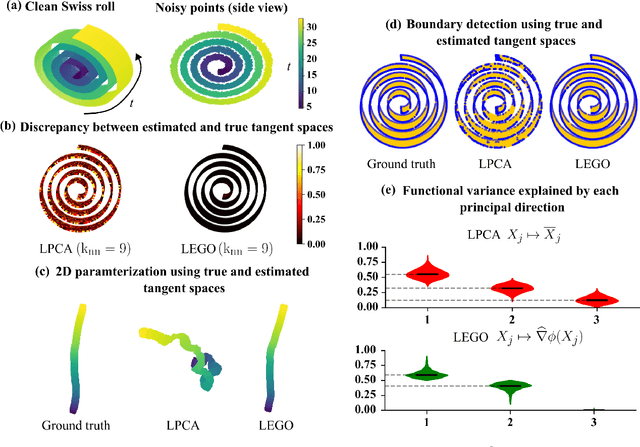
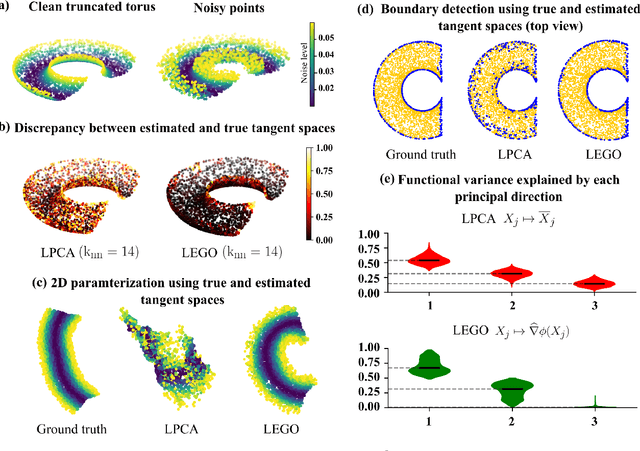
Estimating the tangent spaces of a data manifold is a fundamental problem in data analysis. The standard approach, Local Principal Component Analysis (LPCA), struggles in high-noise settings due to a critical trade-off in choosing the neighborhood size. Selecting an optimal size requires prior knowledge of the geometric and noise characteristics of the data that are often unavailable. In this paper, we propose a spectral method, Laplacian Eigenvector Gradient Orthogonalization (LEGO), that utilizes the global structure of the data to guide local tangent space estimation. Instead of relying solely on local neighborhoods, LEGO estimates the tangent space at each data point by orthogonalizing the gradients of low-frequency eigenvectors of the graph Laplacian. We provide two theoretical justifications of our method. First, a differential geometric analysis on a tubular neighborhood of a manifold shows that gradients of the low-frequency Laplacian eigenfunctions of the tube align closely with the manifold's tangent bundle, while an eigenfunction with high gradient in directions orthogonal to the manifold lie deeper in the spectrum. Second, a random matrix theoretic analysis also demonstrates that low-frequency eigenvectors are robust to sub-Gaussian noise. Through comprehensive experiments, we demonstrate that LEGO yields tangent space estimates that are significantly more robust to noise than those from LPCA, resulting in marked improvements in downstream tasks such as manifold learning, boundary detection, and local intrinsic dimension estimation.

Learning Kronecker-Structured Graphs from Smooth Signals

Graph learning, or network inference, is a prominent problem in graph signal processing (GSP). GSP generalizes the Fourier transform to non-Euclidean domains, and graph learning is pivotal to applying GSP when these domains are unknown. With the recent prevalence of multi-way data, there has been growing interest in product graphs that naturally factorize dependencies across different ways. However, the types of graph products that can be learned are still limited for modeling diverse dependency structures. In this paper, we study the problem of learning a Kronecker-structured product graph from smooth signals. Unlike the more commonly used Cartesian product, the Kronecker product models dependencies in a more intricate, non-separable way, but posits harder constraints on the graph learning problem. To tackle this non-convex problem, we propose an alternating scheme to optimize each factor graph and provide theoretical guarantees for its asymptotic convergence. The proposed algorithm is also modified to learn factor graphs of the strong product. We conduct experiments on synthetic and real-world graphs and demonstrate our approach's efficacy and superior performance compared to existing methods.

Robust Graph-Based Semi-Supervised Learning via $p$-Conductances

We study the problem of semi-supervised learning on graphs in the regime where data labels are scarce or possibly corrupted. We propose an approach called $p$-conductance learning that generalizes the $p$-Laplace and Poisson learning methods by introducing an objective reminiscent of $p$-Laplacian regularization and an affine relaxation of the label constraints. This leads to a family of probability measure mincut programs that balance sparse edge removal with accurate distribution separation. Our theoretical analysis connects these programs to well-known variational and probabilistic problems on graphs (including randomized cuts, effective resistance, and Wasserstein distance) and provides motivation for robustness when labels are diffused via the heat kernel. Computationally, we develop a semismooth Newton-conjugate gradient algorithm and extend it to incorporate class-size estimates when converting the continuous solutions into label assignments. Empirical results on computer vision and citation datasets demonstrate that our approach achieves state-of-the-art accuracy in low label-rate, corrupted-label, and partial-label regimes.

Coupled Hierarchical Structure Learning using Tree-Wasserstein Distance

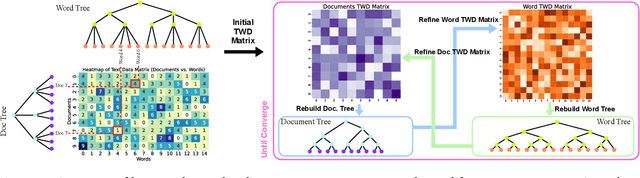
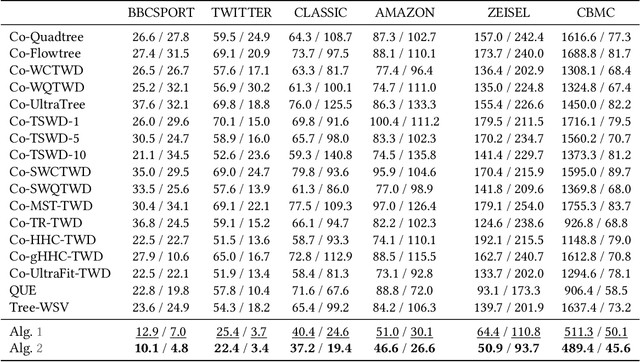
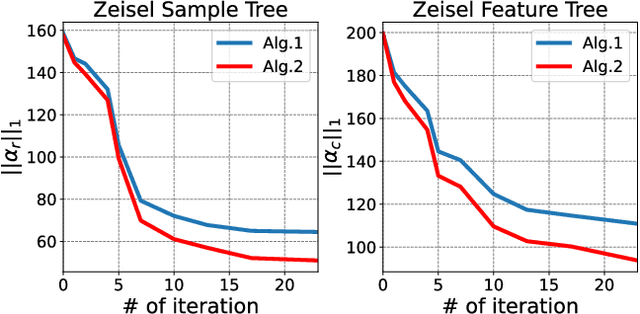
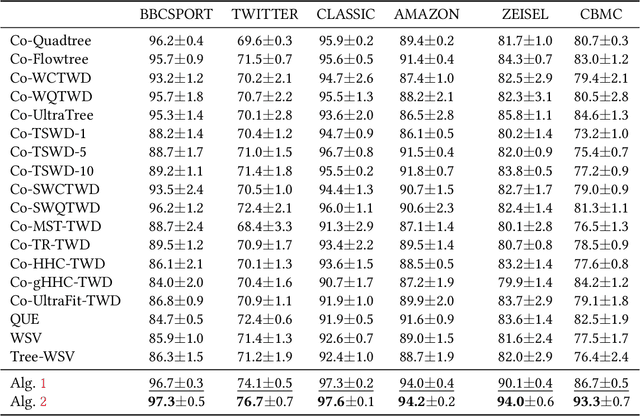
In many applications, both data samples and features have underlying hierarchical structures. However, existing methods for learning these latent structures typically focus on either samples or features, ignoring possible coupling between them. In this paper, we introduce a coupled hierarchical structure learning method using tree-Wasserstein distance (TWD). Our method jointly computes TWDs for samples and features, representing their latent hierarchies as trees. We propose an iterative, unsupervised procedure to build these sample and feature trees based on diffusion geometry, hyperbolic geometry, and wavelet filters. We show that this iterative procedure converges and empirically improves the quality of the constructed trees. The method is also computationally efficient and scales well in high-dimensional settings. Our method can be seamlessly integrated with hyperbolic graph convolutional networks (HGCN). We demonstrate that our method outperforms competing approaches in sparse approximation and unsupervised Wasserstein distance learning on several word-document and single-cell RNA-sequencing datasets. In addition, integrating our method into HGCN enhances performance in link prediction and node classification tasks.

Elucidating Flow Matching ODE Dynamics with respect to Data Geometries

Diffusion-based generative models have become the standard for image generation. ODE-based samplers and flow matching models improve efficiency, in comparison to diffusion models, by reducing sampling steps through learned vector fields. However, the theoretical foundations of flow matching models remain limited, particularly regarding the convergence of individual sample trajectories at terminal time - a critical property that impacts sample quality and being critical assumption for models like the consistency model. In this paper, we advance the theory of flow matching models through a comprehensive analysis of sample trajectories, centered on the denoiser that drives ODE dynamics. We establish the existence, uniqueness and convergence of ODE trajectories at terminal time, ensuring stable sampling outcomes under minimal assumptions. Our analysis reveals how trajectories evolve from capturing global data features to local structures, providing the geometric characterization of per-sample behavior in flow matching models. We also explain the memorization phenomenon in diffusion-based training through our terminal time analysis. These findings bridge critical gaps in understanding flow matching models, with practical implications for sampling stability and model design.

Tree-Wasserstein Distance for High Dimensional Data with a Latent Feature Hierarchy

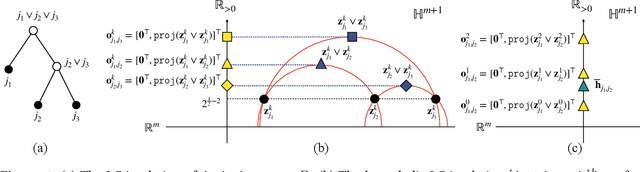
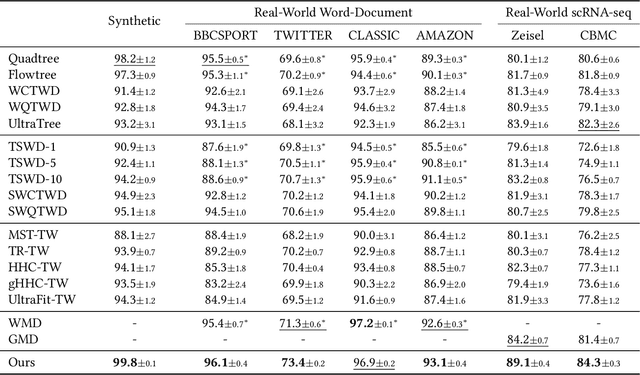
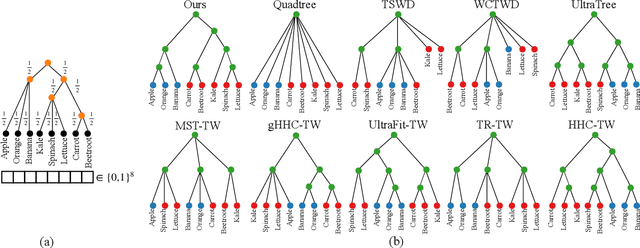
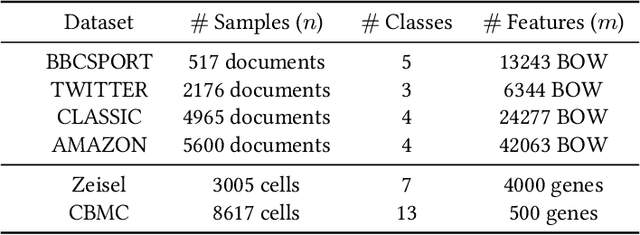
Finding meaningful distances between high-dimensional data samples is an important scientific task. To this end, we propose a new tree-Wasserstein distance (TWD) for high-dimensional data with two key aspects. First, our TWD is specifically designed for data with a latent feature hierarchy, i.e., the features lie in a hierarchical space, in contrast to the usual focus on embedding samples in hyperbolic space. Second, while the conventional use of TWD is to speed up the computation of the Wasserstein distance, we use its inherent tree as a means to learn the latent feature hierarchy. The key idea of our method is to embed the features into a multi-scale hyperbolic space using diffusion geometry and then present a new tree decoding method by establishing analogies between the hyperbolic embedding and trees. We show that our TWD computed based on data observations provably recovers the TWD defined with the latent feature hierarchy and that its computation is efficient and scalable. We showcase the usefulness of the proposed TWD in applications to word-document and single-cell RNA-sequencing datasets, demonstrating its advantages over existing TWDs and methods based on pre-trained models.

Multiway Multislice PHATE: Visualizing Hidden Dynamics of RNNs through Training

Recurrent neural networks (RNNs) are a widely used tool for sequential data analysis, however, they are still often seen as black boxes of computation. Understanding the functional principles of these networks is critical to developing ideal model architectures and optimization strategies. Previous studies typically only emphasize the network representation post-training, overlooking their evolution process throughout training. Here, we present Multiway Multislice PHATE (MM-PHATE), a novel method for visualizing the evolution of RNNs' hidden states. MM-PHATE is a graph-based embedding using structured kernels across the multiple dimensions spanned by RNNs: time, training epoch, and units. We demonstrate on various datasets that MM-PHATE uniquely preserves hidden representation community structure among units and identifies information processing and compression phases during training. The embedding allows users to look under the hood of RNNs across training and provides an intuitive and comprehensive strategy to understanding the network's internal dynamics and draw conclusions, e.g., on why and how one model outperforms another or how a specific architecture might impact an RNN's learning ability.

Comparing Graph Transformers via Positional Encodings

The distinguishing power of graph transformers is closely tied to the choice of positional encoding: features used to augment the base transformer with information about the graph. There are two primary types of positional encoding: absolute positional encodings (APEs) and relative positional encodings (RPEs). APEs assign features to each node and are given as input to the transformer. RPEs instead assign a feature to each pair of nodes, e.g., graph distance, and are used to augment the attention block. A priori, it is unclear which method is better for maximizing the power of the resulting graph transformer. In this paper, we aim to understand the relationship between these different types of positional encodings. Interestingly, we show that graph transformers using APEs and RPEs are equivalent in terms of distinguishing power. In particular, we demonstrate how to interchange APEs and RPEs while maintaining their distinguishing power in terms of graph transformers. Based on our theoretical results, we provide a study on several APEs and RPEs (including the resistance distance and the recently introduced stable and expressive positional encoding (SPE)) and compare their distinguishing power in terms of transformers. We believe our work will help navigate the huge number of choices of positional encoding and will provide guidance on the future design of positional encodings for graph transformers.

Deep and shallow data science for multi-scale optical neuroscience

Optical imaging of the brain has expanded dramatically in the past two decades. New optics, indicators, and experimental paradigms are now enabling in-vivo imaging from the synaptic to the cortex-wide scales. To match the resulting flood of data across scales, computational methods are continuously being developed to meet the need of extracting biologically relevant information. In this pursuit, challenges arise in some domains (e.g., SNR and resolution limits in micron-scale data) that require specialized algorithms. These algorithms can, for example, make use of state-of-the-art machine learning to maximally learn the details of a given scale to optimize the processing pipeline. In contrast, other methods, however, such as graph signal processing, seek to abstract away from some of the details that are scale-specific to provide solutions to specific sub-problems common across scales of neuroimaging. Here we discuss limitations and tradeoffs in algorithmic design with the goal of identifying how data quality and variability can hamper algorithm use and dissemination.