ReFORM: Reflected Flows for On-support Offline RL via Noise Manipulation

Offline reinforcement learning (RL) aims to learn the optimal policy from a fixed dataset generated by behavior policies without additional environment interactions. One common challenge that arises in this setting is the out-of-distribution (OOD) error, which occurs when the policy leaves the training distribution. Prior methods penalize a statistical distance term to keep the policy close to the behavior policy, but this constrains policy improvement and may not completely prevent OOD actions. Another challenge is that the optimal policy distribution can be multimodal and difficult to represent. Recent works apply diffusion or flow policies to address this problem, but it is unclear how to avoid OOD errors while retaining policy expressiveness. We propose ReFORM, an offline RL method based on flow policies that enforces the less restrictive support constraint by construction. ReFORM learns a behavior cloning (BC) flow policy with a bounded source distribution to capture the support of the action distribution, then optimizes a reflected flow that generates bounded noise for the BC flow while keeping the support, to maximize the performance. Across 40 challenging tasks from the OGBench benchmark with datasets of varying quality and using a constant set of hyperparameters for all tasks, ReFORM dominates all baselines with hand-tuned hyperparameters on the performance profile curves.

Solving Multi-Agent Safe Optimal Control with Distributed Epigraph Form MARL

Tasks for multi-robot systems often require the robots to collaborate and complete a team goal while maintaining safety. This problem is usually formalized as a constrained Markov decision process (CMDP), which targets minimizing a global cost and bringing the mean of constraint violation below a user-defined threshold. Inspired by real-world robotic applications, we define safety as zero constraint violation. While many safe multi-agent reinforcement learning (MARL) algorithms have been proposed to solve CMDPs, these algorithms suffer from unstable training in this setting. To tackle this, we use the epigraph form for constrained optimization to improve training stability and prove that the centralized epigraph form problem can be solved in a distributed fashion by each agent. This results in a novel centralized training distributed execution MARL algorithm named Def-MARL. Simulation experiments on 8 different tasks across 2 different simulators show that Def-MARL achieves the best overall performance, satisfies safety constraints, and maintains stable training. Real-world hardware experiments on Crazyflie quadcopters demonstrate the ability of Def-MARL to safely coordinate agents to complete complex collaborative tasks compared to other methods.

Graph Inference with Effective Resistance Queries

The goal of graph inference is to design algorithms for learning properties of a hidden graph using queries to an oracle that returns information about the graph. Graph reconstruction, verification, and property testing are all types of graph inference. In this work, we study graph inference using an oracle that returns the effective resistance (ER) between a pair of vertices. Effective resistance is a distance originating from the study of electrical circuits with many applications. However, ER has received little attention from a graph inference perspective. Indeed, although it is known that an $n$-vertex graph can be uniquely reconstructed from all $\binom{n}{2}$ possible ER queries, little else is known. We address this gap with several new results, including: 1. $O(n)$-query algorithms for testing whether a graph is a tree; deciding whether two graphs are equal assuming one is a subgraph of the other; and testing whether a given vertex (or edge) is a cut vertex (or cut edge). 2. Property testing algorithms, including for testing whether a graph is vertex- or edge-biconnected. We also give a reduction to adapt property testing results from the bounded-degree model to our ER query model. This yields ER-query-based algorithms for testing $k$-connectivity, bipartiteness, planarity, and containment of a fixed subgraph. 3. Graph reconstruction algorithms, including an algorithm for reconstructing a graph from a low-width tree decomposition; a $\Theta(k^2)$-query, polynomial-time algorithm for recovering the adjacency matrix $A$ of a hidden graph, given $A$ with $k$ of its entries deleted; and a $k$-query, exponential-time algorithm for the same task. We also compare the power of ER queries and shortest path queries, which are closely related but better studied. Interestingly, we show that the two query models are incomparable in power.

Discrete GCBF Proximal Policy Optimization for Multi-agent Safe Optimal Control

Control policies that can achieve high task performance and satisfy safety constraints are desirable for any system, including multi-agent systems (MAS). One promising technique for ensuring the safety of MAS is distributed control barrier functions (CBF). However, it is difficult to design distributed CBF-based policies for MAS that can tackle unknown discrete-time dynamics, partial observability, changing neighborhoods, and input constraints, especially when a distributed high-performance nominal policy that can achieve the task is unavailable. To tackle these challenges, we propose DGPPO, a new framework that simultaneously learns both a discrete graph CBF which handles neighborhood changes and input constraints, and a distributed high-performance safe policy for MAS with unknown discrete-time dynamics. We empirically validate our claims on a suite of multi-agent tasks spanning three different simulation engines. The results suggest that, compared with existing methods, our DGPPO framework obtains policies that achieve high task performance (matching baselines that ignore the safety constraints), and high safety rates (matching the most conservative baselines), with a constant set of hyperparameters across all environments.

Risk-aware MPPI for Stochastic Hybrid Systems

Path Planning for stochastic hybrid systems presents a unique challenge of predicting distributions of future states subject to a state-dependent dynamics switching function. In this work, we propose a variant of Model Predictive Path Integral Control (MPPI) to plan kinodynamic paths for such systems. Monte Carlo may be inaccurate when few samples are chosen to predict future states under state-dependent disturbances. We employ recently proposed Unscented Transform-based methods to capture stochasticity in the states as well as the state-dependent switching surfaces. This is in contrast to previous works that perform switching based only on the mean of predicted states. We focus our motion planning application on the navigation of a mobile robot in the presence of dynamically moving agents whose responses are based on sensor-constrained attention zones. We evaluate our framework on a simulated mobile robot and show faster convergence to a goal without collisions when the robot exploits the hybrid human dynamics versus when it does not.

RPCBF: Constructing Safety Filters Robust to Model Error and Disturbances via Policy Control Barrier Functions

Control Barrier Functions (CBFs) have proven to be an effective tool for performing safe control synthesis for nonlinear systems. However, guaranteeing safety in the presence of disturbances and input constraints for high relative degree systems is a difficult problem. In this work, we propose the Robust Policy CBF (RPCBF), a practical method of constructing CBF approximations that is easy to implement and robust to disturbances via the estimation of a value function. We demonstrate the effectiveness of our method in simulation on a variety of high relative degree input-constrained systems. Finally, we demonstrate the benefits of RPCBF in compensating for model errors on a hardware quadcopter platform by treating the model errors as disturbances. The project page can be found at https://oswinso.xyz/rpcbf.

Model Predictive Path Integral Methods with Reach-Avoid Tasks and Control Barrier Functions

The rapid advancement of robotics necessitates robust tools for developing and testing safe control architectures in dynamic and uncertain environments. Ensuring safety and reliability in robotics, especially in safety-critical applications, is crucial, driving substantial industrial and academic efforts. In this context, we extend CBFkit, a Python/ROS2 toolbox, which now incorporates a planner using reach-avoid specifications as a cost function. This integration with the Model Predictive Path Integral (MPPI) controllers enables the toolbox to satisfy complex tasks while ensuring formal safety guarantees under various sources of uncertainty using Control Barrier Functions (CBFs). CBFkit is optimized for speed using JAX for automatic differentiation and jaxopt for quadratic program solving. The toolbox supports various robotic applications, including autonomous navigation, human-robot interaction, and multi-robot coordination. The toolbox also offers a comprehensive library of planner, controller, sensor, and estimator implementations. Through a series of examples, we demonstrate the enhanced capabilities of CBFkit in different robotic scenarios.

Biharmonic Distance of Graphs and its Higher-Order Variants: Theoretical Properties with Applications to Centrality and Clustering

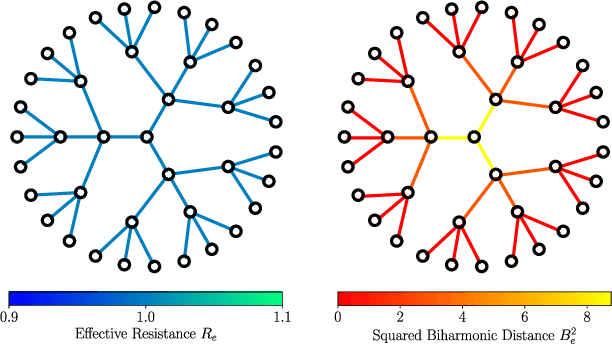
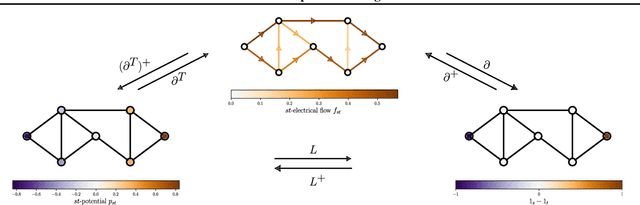
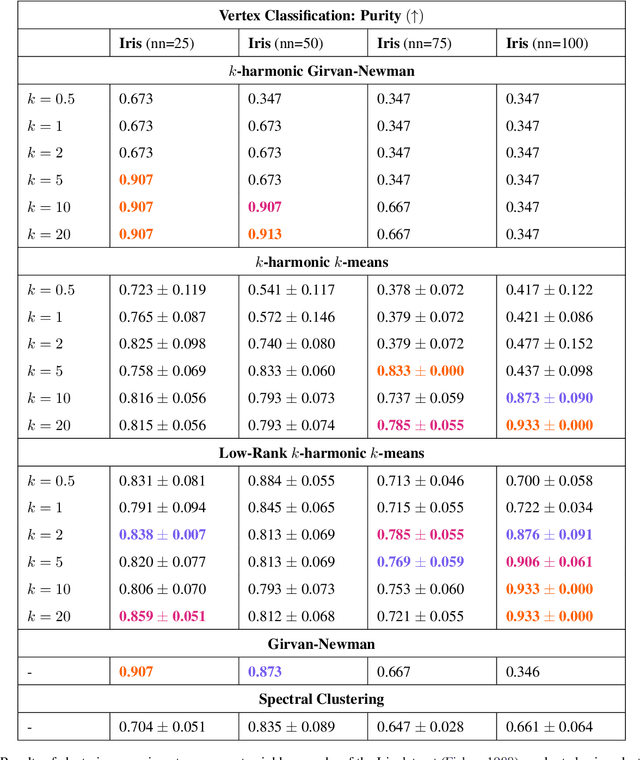
Effective resistance is a distance between vertices of a graph that is both theoretically interesting and useful in applications. We study a variant of effective resistance called the biharmonic distance. While the effective resistance measures how well-connected two vertices are, we prove several theoretical results supporting the idea that the biharmonic distance measures how important an edge is to the global topology of the graph. Our theoretical results connect the biharmonic distance to well-known measures of connectivity of a graph like its total resistance and sparsity. Based on these results, we introduce two clustering algorithms using the biharmonic distance. Finally, we introduce a further generalization of the biharmonic distance that we call the $k$-harmonic distance. We empirically study the utility of biharmonic and $k$-harmonic distance for edge centrality and graph clustering.

CBFKIT: A Control Barrier Function Toolbox for Robotics Applications

This paper introduces CBFKit, a Python/ROS toolbox for safe robotics planning and control under uncertainty. The toolbox provides a general framework for designing control barrier functions for mobility systems within both deterministic and stochastic environments. It can be connected to the ROS open-source robotics middleware, allowing for the setup of multi-robot applications, encoding of environments and maps, and integrations with predictive motion planning algorithms. Additionally, it offers multiple CBF variations and algorithms for robot control. The CBFKit is demonstrated on the Toyota Human Support Robot (HSR) in both simulation and in physical experiments.

Comparing Graph Transformers via Positional Encodings

The distinguishing power of graph transformers is closely tied to the choice of positional encoding: features used to augment the base transformer with information about the graph. There are two primary types of positional encoding: absolute positional encodings (APEs) and relative positional encodings (RPEs). APEs assign features to each node and are given as input to the transformer. RPEs instead assign a feature to each pair of nodes, e.g., graph distance, and are used to augment the attention block. A priori, it is unclear which method is better for maximizing the power of the resulting graph transformer. In this paper, we aim to understand the relationship between these different types of positional encodings. Interestingly, we show that graph transformers using APEs and RPEs are equivalent in terms of distinguishing power. In particular, we demonstrate how to interchange APEs and RPEs while maintaining their distinguishing power in terms of graph transformers. Based on our theoretical results, we provide a study on several APEs and RPEs (including the resistance distance and the recently introduced stable and expressive positional encoding (SPE)) and compare their distinguishing power in terms of transformers. We believe our work will help navigate the huge number of choices of positional encoding and will provide guidance on the future design of positional encodings for graph transformers.