BR-MPPI: Barrier Rate guided MPPI for Enforcing Multiple Inequality Constraints with Learned Signed Distance Field

Model Predictive Path Integral (MPPI) controller is used to solve unconstrained optimal control problems and Control Barrier Function (CBF) is a tool to impose strict inequality constraints, a.k.a, barrier constraints. In this work, we propose an integration of these two methods that employ CBF-like conditions to guide the control sampling procedure of MPPI. CBFs provide an inequality constraint restricting the rate of change of barrier functions by a classK function of the barrier itself. We instead impose the CBF condition as an equality constraint by choosing a parametric linear classK function and treating this parameter as a state in an augmented system. The time derivative of this parameter acts as an additional control input that is designed by MPPI. A cost function is further designed to reignite Nagumo's theorem at the boundary of the safe set by promoting specific values of classK parameter to enforce safety. Our problem formulation results in an MPPI subject to multiple state and control-dependent equality constraints which are non-trivial to satisfy with randomly sampled control inputs. We therefore also introduce state transformations and control projection operations, inspired by the literature on path planning for manifolds, to resolve the aforementioned issue. We show empirically through simulations and experiments on quadrotor that our proposed algorithm exhibits better sampled efficiency and enhanced capability to operate closer to the safe set boundary over vanilla MPPI.

MRTA-Sim: A Modular Simulator for Multi-Robot Allocation, Planning, and Control in Open-World Environments

This paper introduces MRTA-Sim, a Python/ROS2/Gazebo simulator for testing approaches to Multi-Robot Task Allocation (MRTA) problems on simulated robots in complex, indoor environments. Grid-based approaches to MRTA problems can be too restrictive for use in complex, dynamic environments such in warehouses, department stores, hospitals, etc. However, approaches that operate in free-space often operate at a layer of abstraction above the control and planning layers of a robot and make an assumption on approximate travel time between points of interest in the system. These abstractions can neglect the impact of the tight space and multi-agent interactions on the quality of the solution. Therefore, MRTA solutions should be tested with the navigation stacks of the robots in mind, taking into account robot planning, conflict avoidance between robots, and human interaction and avoidance. This tool connects the allocation output of MRTA solvers to individual robot planning using the NAV2 stack and local, centralized multi-robot deconfliction using Control Barrier Function-Quadrtic Programs (CBF-QPs), creating a platform closer to real-world operation for more comprehensive testing of these approaches. The simulation architecture is modular so that users can swap out methods at different levels of the stack. We show the use of our system with a Satisfiability Modulo Theories (SMT)-based approach to dynamic MRTA on a fleet of indoor delivery robots.

Enabling Safety for Aerial Robots: Planning and Control Architectures

Ensuring safe autonomy is crucial for deploying aerial robots in real-world applications. However, safety is a multifaceted challenge that must be addressed from multiple perspectives, including navigation in dynamic environments, operation under resource constraints, and robustness against adversarial attacks and uncertainties. In this paper, we present the authors' recent work that tackles some of these challenges and highlights key aspects that must be considered to enhance the safety and performance of autonomous aerial systems. All presented approaches are validated through hardware experiments.

Risk-aware MPPI for Stochastic Hybrid Systems

Path Planning for stochastic hybrid systems presents a unique challenge of predicting distributions of future states subject to a state-dependent dynamics switching function. In this work, we propose a variant of Model Predictive Path Integral Control (MPPI) to plan kinodynamic paths for such systems. Monte Carlo may be inaccurate when few samples are chosen to predict future states under state-dependent disturbances. We employ recently proposed Unscented Transform-based methods to capture stochasticity in the states as well as the state-dependent switching surfaces. This is in contrast to previous works that perform switching based only on the mean of predicted states. We focus our motion planning application on the navigation of a mobile robot in the presence of dynamically moving agents whose responses are based on sensor-constrained attention zones. We evaluate our framework on a simulated mobile robot and show faster convergence to a goal without collisions when the robot exploits the hybrid human dynamics versus when it does not.

Neural Configuration Distance Function for Continuum Robot Control

This paper presents a novel method for modeling the shape of a continuum robot as a Neural Configuration Euclidean Distance Function (N-CEDF). By learning separate distance fields for each link and combining them through the kinematics chain, the learned N-CEDF provides an accurate and computationally efficient representation of the robot's shape. The key advantage of a distance function representation of a continuum robot is that it enables efficient collision checking for motion planning in dynamic and cluttered environments, even with point-cloud observations. We integrate the N-CEDF into a Model Predictive Path Integral (MPPI) controller to generate safe trajectories. The proposed approach is validated for continuum robots with various links in several simulated environments with static and dynamic obstacles.

Model Predictive Path Integral Methods with Reach-Avoid Tasks and Control Barrier Functions

The rapid advancement of robotics necessitates robust tools for developing and testing safe control architectures in dynamic and uncertain environments. Ensuring safety and reliability in robotics, especially in safety-critical applications, is crucial, driving substantial industrial and academic efforts. In this context, we extend CBFkit, a Python/ROS2 toolbox, which now incorporates a planner using reach-avoid specifications as a cost function. This integration with the Model Predictive Path Integral (MPPI) controllers enables the toolbox to satisfy complex tasks while ensuring formal safety guarantees under various sources of uncertainty using Control Barrier Functions (CBFs). CBFkit is optimized for speed using JAX for automatic differentiation and jaxopt for quadratic program solving. The toolbox supports various robotic applications, including autonomous navigation, human-robot interaction, and multi-robot coordination. The toolbox also offers a comprehensive library of planner, controller, sensor, and estimator implementations. Through a series of examples, we demonstrate the enhanced capabilities of CBFkit in different robotic scenarios.

A Constructive Method for Designing Safe Multirate Controllers for Differentially-Flat Systems

We present a multi-rate control architecture that leverages fundamental properties of differential flatness to synthesize controllers for safety-critical nonlinear dynamical systems. We propose a two-layer architecture, where the high-level generates reference trajectories using a linear Model Predictive Controller, and the low-level tracks this reference using a feedback controller. The novelty lies in how we couple these layers, to achieve formal guarantees on recursive feasibility of the MPC problem, and safety of the nonlinear system. Furthermore, using differential flatness, we provide a constructive means to synthesize the multi-rate controller, thereby removing the need to search for suitable Lyapunov or barrier functions, or to approximately linearize/discretize nonlinear dynamics. We show the synthesized controller is a convex optimization problem, making it amenable to real-time implementations. The method is demonstrated experimentally on a ground rover and a quadruped robotic system.

Feasible Space Monitoring for Multiple Control Barrier Functions with application to Large Scale Indoor Navigation

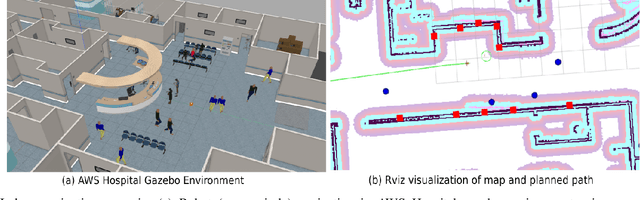
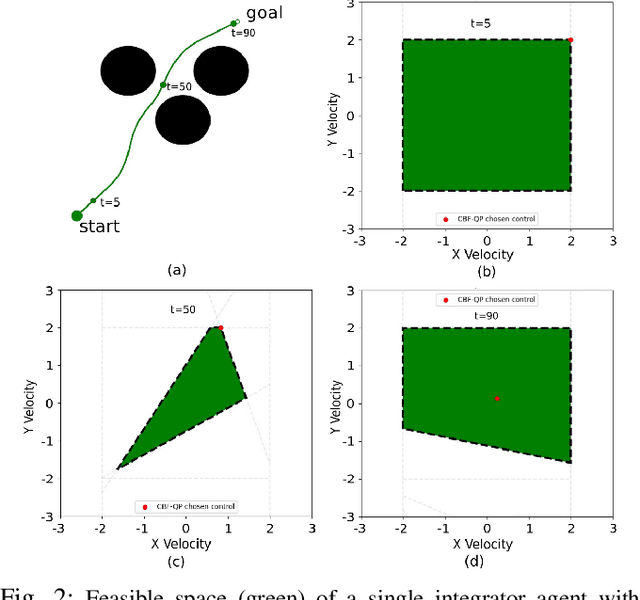
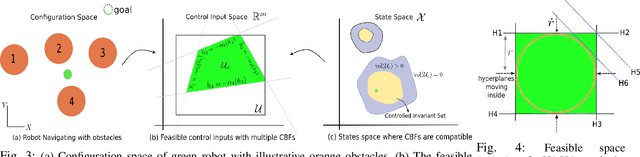
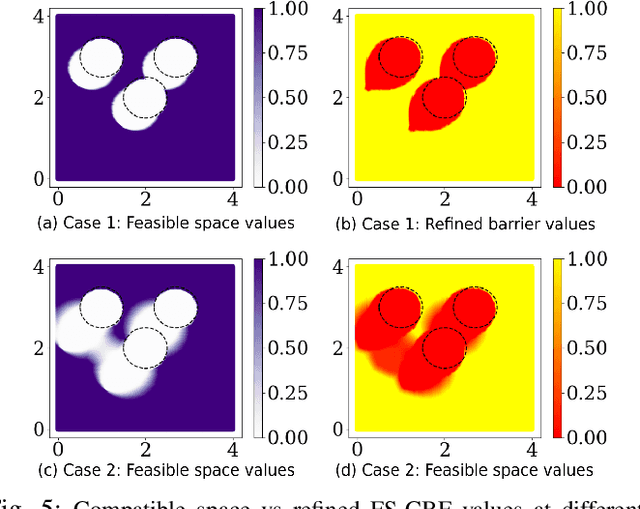
Quadratic programs (QP) subject to multiple time-dependent control barrier function (CBF) based constraints have been used to design safety-critical controllers. However, ensuring the existence of a solution at all times to the QP subject to multiple CBF constraints is non-trivial. We quantify the feasible solution space of the QP in terms of its volume. We introduce a novel feasible space volume monitoring control barrier function that promotes compatibility of barrier functions and, hence, existence of a solution at all times. We show empirically that our approach not only enhances feasibility but also exhibits reduced sensitivity to changes in the hyperparameters such as gains of nominal controller. Finally, paired with a global planner, we evaluate our controller for navigation among humans in the AWS Hospital gazebo environment. The proposed controller is demonstrated to outperform the standard CBF-QP controller in maintaining feasibility.

The Dilemma of Choice: Addressing Constraint Selection for Autonomous Robotic Agents

The tasks that an autonomous agent is expected to perform are often optional or are incompatible with each other owing to the agent's limited actuation capabilities, specifically the dynamics and control input bounds. We encode tasks as time-dependent state constraints and leverage the advances in multi-objective optimization to formulate the problem of choosing tasks as selection of a feasible subset of constraints that can be satisfied for all time and maximizes a performance metric. We show that this problem, although amenable to reachability or mixed integer model predictive control-based analysis in the offline phase, is NP-Hard in general and therefore requires heuristics to be solved efficiently. When incompatibility in constraints is observed under a given policy that imposes task constraints at each time step in an optimization problem, we assign a Lagrange score to each of these constraints based on the variation in the corresponding Lagrange multipliers over the compatible time horizon. These scores are then used to decide the order in which constraints are dropped in a greedy strategy. We further employ a genetic algorithm to improve upon the greedy strategy. We evaluate our method on a robot waypoint following task when the low-level controllers that impose state constraints are described by Control Barrier Function-based Quadratic Programs and provide a comparison with waypoint selection based on knowledge of backward reachable sets.

Rate-Tunable Control Barrier Functions: Methods and Algorithms for Online Adaptation

Control Barrier Functions offer safety certificates by dictating controllers that enforce safety constraints. However, their response depends on the classK function that is used to restrict the rate of change of the barrier function along the system trajectories. This paper introduces the notion of Rate Tunable Control Barrier Function (RT-CBF), which allows for online tuning of the response of CBF-based controllers. In contrast to the existing CBF approaches that use a fixed (predefined) classK function to ensure safety, we parameterize and adapt the classK function parameters online. Furthermore, we discuss the challenges associated with multiple barrier constraints, namely ensuring that they admit a common control input that satisfies them simultaneously for all time. In practice, RT-CBF enables designing parameter dynamics for (1) a better-performing response, where performance is defined in terms of the cost accumulated over a time horizon, or (2) a less conservative response. We propose a model-predictive framework that computes the sensitivity of the future states with respect to the parameters and uses Sequential Quadratic Programming for deriving an online law to update the parameters in the direction of improving the performance. When prediction is not possible, we also provide point-wise sufficient conditions to be imposed on any user-given parameter dynamics so that multiple CBF constraints continue to admit common control input with time. Finally, we introduce RT-CBFs for decentralized uncooperative multi-agent systems, where a trust factor, computed based on the instantaneous ease of constraint satisfaction, is used to update parameters online for a less conservative response.