Precise Zero-Shot Pointwise Ranking with LLMs through Post-Aggregated Global Context Information

Recent advancements have successfully harnessed the power of Large Language Models (LLMs) for zero-shot document ranking, exploring a variety of prompting strategies. Comparative approaches like pairwise and listwise achieve high effectiveness but are computationally intensive and thus less practical for larger-scale applications. Scoring-based pointwise approaches exhibit superior efficiency by independently and simultaneously generating the relevance scores for each candidate document. However, this independence ignores critical comparative insights between documents, resulting in inconsistent scoring and suboptimal performance. In this paper, we aim to improve the effectiveness of pointwise methods while preserving their efficiency through two key innovations: (1) We propose a novel Global-Consistent Comparative Pointwise Ranking (GCCP) strategy that incorporates global reference comparisons between each candidate and an anchor document to generate contrastive relevance scores. We strategically design the anchor document as a query-focused summary of pseudo-relevant candidates, which serves as an effective reference point by capturing the global context for document comparison. (2) These contrastive relevance scores can be efficiently Post-Aggregated with existing pointwise methods, seamlessly integrating essential Global Context information in a training-free manner (PAGC). Extensive experiments on the TREC DL and BEIR benchmark demonstrate that our approach significantly outperforms previous pointwise methods while maintaining comparable efficiency. Our method also achieves competitive performance against comparative methods that require substantially more computational resources. More analyses further validate the efficacy of our anchor construction strategy.

BR-MPPI: Barrier Rate guided MPPI for Enforcing Multiple Inequality Constraints with Learned Signed Distance Field

Model Predictive Path Integral (MPPI) controller is used to solve unconstrained optimal control problems and Control Barrier Function (CBF) is a tool to impose strict inequality constraints, a.k.a, barrier constraints. In this work, we propose an integration of these two methods that employ CBF-like conditions to guide the control sampling procedure of MPPI. CBFs provide an inequality constraint restricting the rate of change of barrier functions by a classK function of the barrier itself. We instead impose the CBF condition as an equality constraint by choosing a parametric linear classK function and treating this parameter as a state in an augmented system. The time derivative of this parameter acts as an additional control input that is designed by MPPI. A cost function is further designed to reignite Nagumo's theorem at the boundary of the safe set by promoting specific values of classK parameter to enforce safety. Our problem formulation results in an MPPI subject to multiple state and control-dependent equality constraints which are non-trivial to satisfy with randomly sampled control inputs. We therefore also introduce state transformations and control projection operations, inspired by the literature on path planning for manifolds, to resolve the aforementioned issue. We show empirically through simulations and experiments on quadrotor that our proposed algorithm exhibits better sampled efficiency and enhanced capability to operate closer to the safe set boundary over vanilla MPPI.

Certifying Stability of Reinforcement Learning Policies using Generalized Lyapunov Functions

We study the problem of certifying the stability of closed-loop systems under control policies derived from optimal control or reinforcement learning (RL). Classical Lyapunov methods require a strict step-wise decrease in the Lyapunov function but such a certificate is difficult to construct for a learned control policy. The value function associated with an RL policy is a natural Lyapunov function candidate but it is not clear how it should be modified. To gain intuition, we first study the linear quadratic regulator (LQR) problem and make two key observations. First, a Lyapunov function can be obtained from the value function of an LQR policy by augmenting it with a residual term related to the system dynamics and stage cost. Second, the classical Lyapunov decrease requirement can be relaxed to a generalized Lyapunov condition requiring only decrease on average over multiple time steps. Using this intuition, we consider the nonlinear setting and formulate an approach to learn generalized Lyapunov functions by augmenting RL value functions with neural network residual terms. Our approach successfully certifies the stability of RL policies trained on Gymnasium and DeepMind Control benchmarks. We also extend our method to jointly train neural controllers and stability certificates using a multi-step Lyapunov loss, resulting in larger certified inner approximations of the region of attraction compared to the classical Lyapunov approach. Overall, our formulation enables stability certification for a broad class of systems with learned policies by making certificates easier to construct, thereby bridging classical control theory and modern learning-based methods.

Neural Configuration-Space Barriers for Manipulation Planning and Control

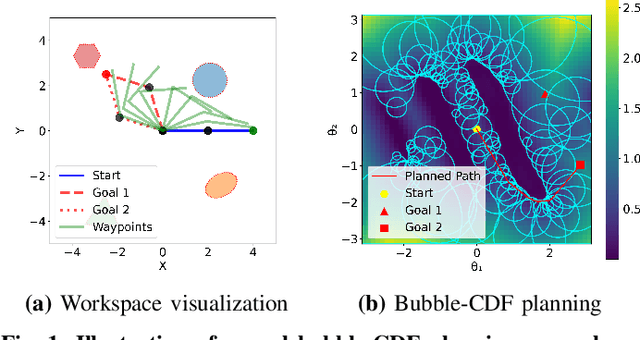
Planning and control for high-dimensional robot manipulators in cluttered, dynamic environments require both computational efficiency and robust safety guarantees. Inspired by recent advances in learning configuration-space distance functions (CDFs) as robot body representations, we propose a unified framework for motion planning and control that formulates safety constraints as CDF barriers. A CDF barrier approximates the local free configuration space, substantially reducing the number of collision-checking operations during motion planning. However, learning a CDF barrier with a neural network and relying on online sensor observations introduce uncertainties that must be considered during control synthesis. To address this, we develop a distributionally robust CDF barrier formulation for control that explicitly accounts for modeling errors and sensor noise without assuming a known underlying distribution. Simulations and hardware experiments on a 6-DoF xArm manipulator show that our neural CDF barrier formulation enables efficient planning and robust real-time safe control in cluttered and dynamic environments, relying only on onboard point-cloud observations.

Neural Configuration Distance Function for Continuum Robot Control

This paper presents a novel method for modeling the shape of a continuum robot as a Neural Configuration Euclidean Distance Function (N-CEDF). By learning separate distance fields for each link and combining them through the kinematics chain, the learned N-CEDF provides an accurate and computationally efficient representation of the robot's shape. The key advantage of a distance function representation of a continuum robot is that it enables efficient collision checking for motion planning in dynamic and cluttered environments, even with point-cloud observations. We integrate the N-CEDF into a Model Predictive Path Integral (MPPI) controller to generate safe trajectories. The proposed approach is validated for continuum robots with various links in several simulated environments with static and dynamic obstacles.

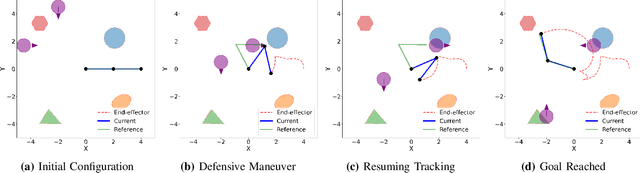
Sensor-Based Distributionally Robust Control for Safe Robot Navigation in Dynamic Environments

We introduce a novel method for safe mobile robot navigation in dynamic, unknown environments, utilizing onboard sensing to impose safety constraints without the need for accurate map reconstruction. Traditional methods typically rely on detailed map information to synthesize safe stabilizing controls for mobile robots, which can be computationally demanding and less effective, particularly in dynamic operational conditions. By leveraging recent advances in distributionally robust optimization, we develop a distributionally robust control barrier function (DR-CBF) constraint that directly processes range sensor data to impose safety constraints. Coupling this with a control Lyapunov function (CLF) for path tracking, we demonstrate that our CLF-DR-CBF control synthesis method achieves safe, efficient, and robust navigation in uncertain dynamic environments. We demonstrate the effectiveness of our approach in simulated and real autonomous robot navigation experiments, marking a substantial advancement in real-time safety guarantees for mobile robots.

Disentangling Instructive Information from Ranked Multiple Candidates for Multi-Document Scientific Summarization

Automatically condensing multiple topic-related scientific papers into a succinct and concise summary is referred to as Multi-Document Scientific Summarization (MDSS). Currently, while commonly used abstractive MDSS methods can generate flexible and coherent summaries, the difficulty in handling global information and the lack of guidance during decoding still make it challenging to generate better summaries. To alleviate these two shortcomings, this paper introduces summary candidates into MDSS, utilizing the global information of the document set and additional guidance from the summary candidates to guide the decoding process. Our insights are twofold: Firstly, summary candidates can provide instructive information from both positive and negative perspectives, and secondly, selecting higher-quality candidates from multiple options contributes to producing better summaries. Drawing on the insights, we propose a summary candidates fusion framework -- Disentangling Instructive information from Ranked candidates (DIR) for MDSS. Specifically, DIR first uses a specialized pairwise comparison method towards multiple candidates to pick out those of higher quality. Then DIR disentangles the instructive information of summary candidates into positive and negative latent variables with Conditional Variational Autoencoder. These variables are further incorporated into the decoder to guide generation. We evaluate our approach with three different types of Transformer-based models and three different types of candidates, and consistently observe noticeable performance improvements according to automatic and human evaluation. More analyses further demonstrate the effectiveness of our model in handling global information and enhancing decoding controllability.

Distributionally Robust Policy and Lyapunov-Certificate Learning

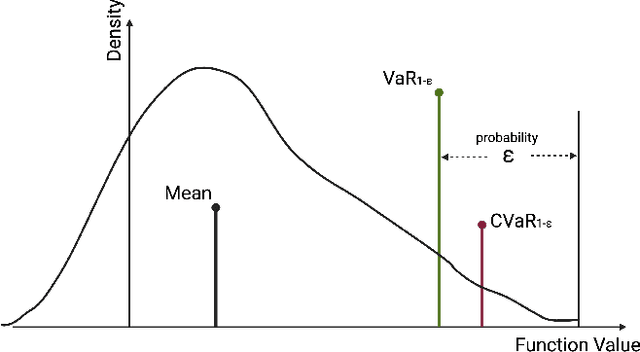
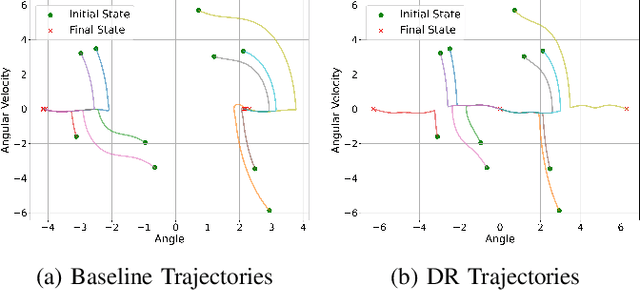
This article presents novel methods for synthesizing distributionally robust stabilizing neural controllers and certificates for control systems under model uncertainty. A key challenge in designing controllers with stability guarantees for uncertain systems is the accurate determination of and adaptation to shifts in model parametric uncertainty during online deployment. We tackle this with a novel distributionally robust formulation of the Lyapunov derivative chance constraint ensuring a monotonic decrease of the Lyapunov certificate. To avoid the computational complexity involved in dealing with the space of probability measures, we identify a sufficient condition in the form of deterministic convex constraints that ensures the Lyapunov derivative constraint is satisfied. We integrate this condition into a loss function for training a neural network-based controller and show that, for the resulting closed-loop system, the global asymptotic stability of its equilibrium can be certified with high confidence, even with Out-of-Distribution (OoD) model uncertainties. To demonstrate the efficacy and efficiency of the proposed methodology, we compare it with an uncertainty-agnostic baseline approach and several reinforcement learning approaches in two control problems in simulation.

Recommending Missed Citations Identified by Reviewers: A New Task, Dataset and Baselines

Citing comprehensively and appropriately has become a challenging task with the explosive growth of scientific publications. Current citation recommendation systems aim to recommend a list of scientific papers for a given text context or a draft paper. However, none of the existing work focuses on already included citations of full papers, which are imperfect and still have much room for improvement. In the scenario of peer reviewing, it is a common phenomenon that submissions are identified as missing vital citations by reviewers. This may lead to a negative impact on the credibility and validity of the research presented. To help improve citations of full papers, we first define a novel task of Recommending Missed Citations Identified by Reviewers (RMC) and construct a corresponding expert-labeled dataset called CitationR. We conduct an extensive evaluation of several state-of-the-art methods on CitationR. Furthermore, we propose a new framework RMCNet with an Attentive Reference Encoder module mining the relevance between papers, already-made citations, and missed citations. Empirical results prove that RMC is challenging, with the proposed architecture outperforming previous methods in all metrics. We release our dataset and benchmark models to motivate future research on this challenging new task.

Safe Stabilizing Control for Polygonal Robots in Dynamic Elliptical Environments

This paper addresses the challenge of safe navigation for rigid-body mobile robots in dynamic environments. We introduce an analytic approach to compute the distance between a polygon and an ellipse, and employ it to construct a control barrier function (CBF) for safe control synthesis. Existing CBF design methods for mobile robot obstacle avoidance usually assume point or circular robots, preventing their applicability to more realistic robot body geometries. Our work enables CBF designs that capture complex robot and obstacle shapes. We demonstrate the effectiveness of our approach in simulations highlighting real-time obstacle avoidance in constrained and dynamic environments for both mobile robots and multi-joint robot arms.