Distributionally Robust Policy and Lyapunov-Certificate Learning
Paper and Code
Apr 03, 2024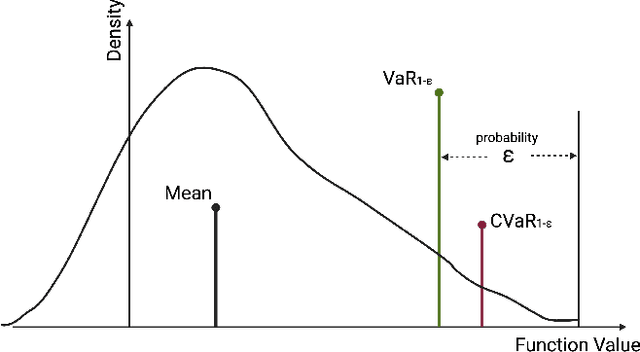
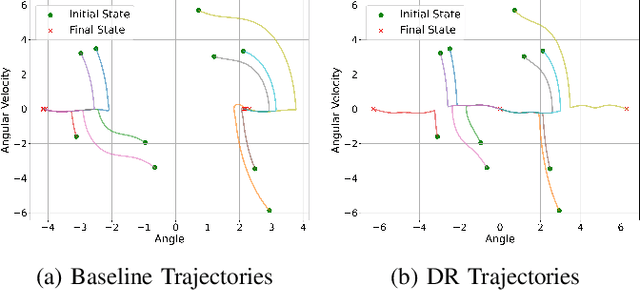


This article presents novel methods for synthesizing distributionally robust stabilizing neural controllers and certificates for control systems under model uncertainty. A key challenge in designing controllers with stability guarantees for uncertain systems is the accurate determination of and adaptation to shifts in model parametric uncertainty during online deployment. We tackle this with a novel distributionally robust formulation of the Lyapunov derivative chance constraint ensuring a monotonic decrease of the Lyapunov certificate. To avoid the computational complexity involved in dealing with the space of probability measures, we identify a sufficient condition in the form of deterministic convex constraints that ensures the Lyapunov derivative constraint is satisfied. We integrate this condition into a loss function for training a neural network-based controller and show that, for the resulting closed-loop system, the global asymptotic stability of its equilibrium can be certified with high confidence, even with Out-of-Distribution (OoD) model uncertainties. To demonstrate the efficacy and efficiency of the proposed methodology, we compare it with an uncertainty-agnostic baseline approach and several reinforcement learning approaches in two control problems in simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge