Koopman Operators in Robot Learning

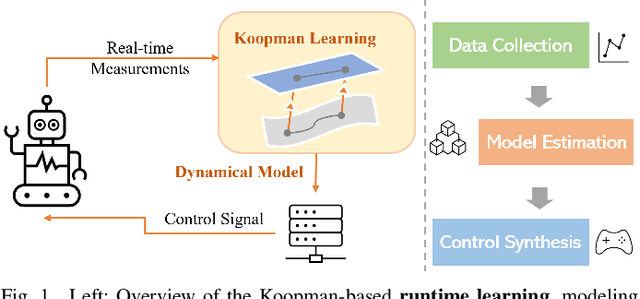
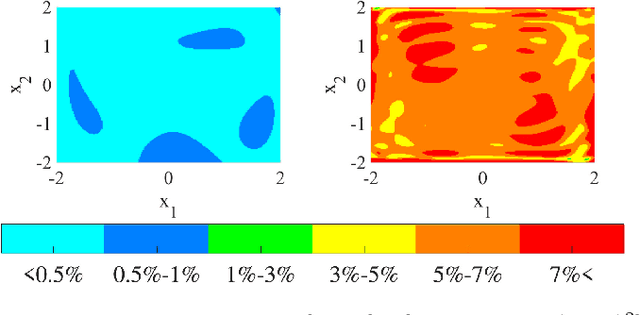
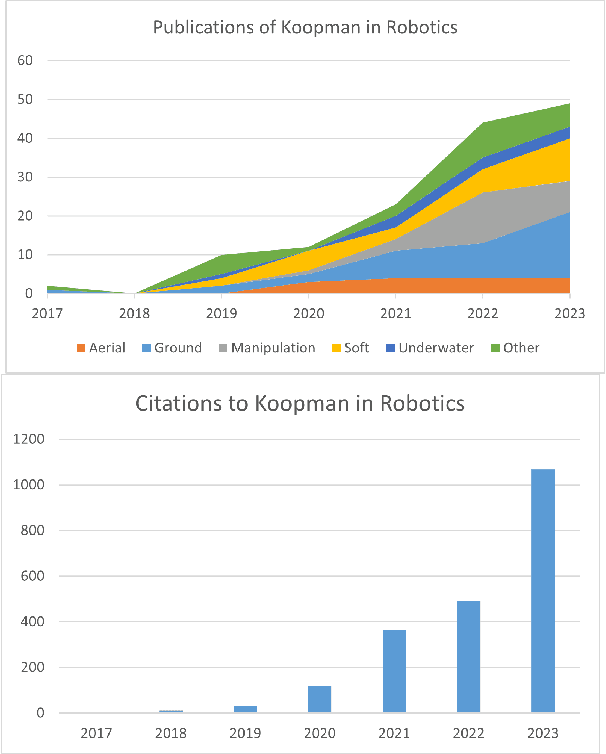
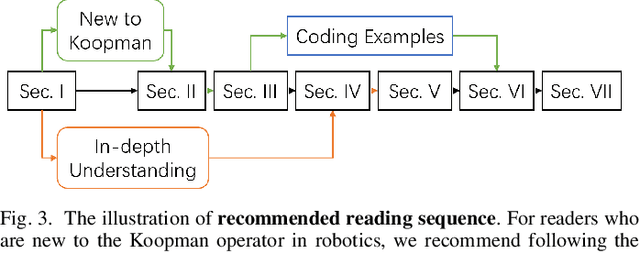
Koopman operator theory offers a rigorous treatment of dynamics and has been emerging as a powerful modeling and learning-based control method enabling significant advancements across various domains of robotics. Due to its ability to represent nonlinear dynamics as a linear operator, Koopman theory offers a fresh lens through which to understand and tackle the modeling and control of complex robotic systems. Moreover, it enables incremental updates and is computationally inexpensive making it particularly appealing for real-time applications and online active learning. This review comprehensively presents recent research results on advancing Koopman operator theory across diverse domains of robotics, encompassing aerial, legged, wheeled, underwater, soft, and manipulator robotics. Furthermore, it offers practical tutorials to help new users get started as well as a treatise of more advanced topics leading to an outlook on future directions and open research questions. Taken together, these provide insights into the potential evolution of Koopman theory as applied to the field of robotics.

Distributionally Robust Policy and Lyapunov-Certificate Learning

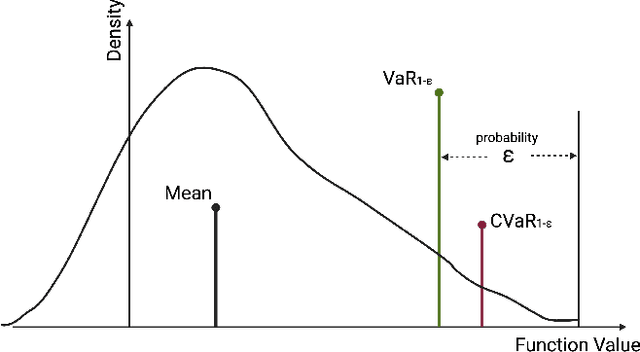
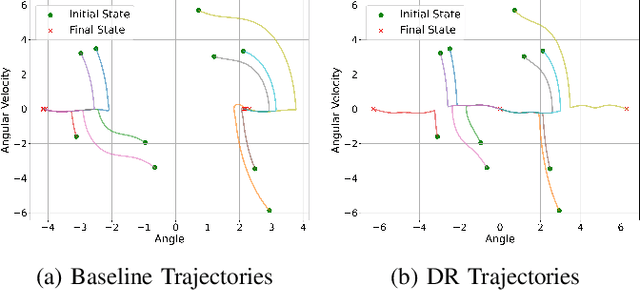
This article presents novel methods for synthesizing distributionally robust stabilizing neural controllers and certificates for control systems under model uncertainty. A key challenge in designing controllers with stability guarantees for uncertain systems is the accurate determination of and adaptation to shifts in model parametric uncertainty during online deployment. We tackle this with a novel distributionally robust formulation of the Lyapunov derivative chance constraint ensuring a monotonic decrease of the Lyapunov certificate. To avoid the computational complexity involved in dealing with the space of probability measures, we identify a sufficient condition in the form of deterministic convex constraints that ensures the Lyapunov derivative constraint is satisfied. We integrate this condition into a loss function for training a neural network-based controller and show that, for the resulting closed-loop system, the global asymptotic stability of its equilibrium can be certified with high confidence, even with Out-of-Distribution (OoD) model uncertainties. To demonstrate the efficacy and efficiency of the proposed methodology, we compare it with an uncertainty-agnostic baseline approach and several reinforcement learning approaches in two control problems in simulation.

Distributionally Robust Lyapunov Function Search Under Uncertainty

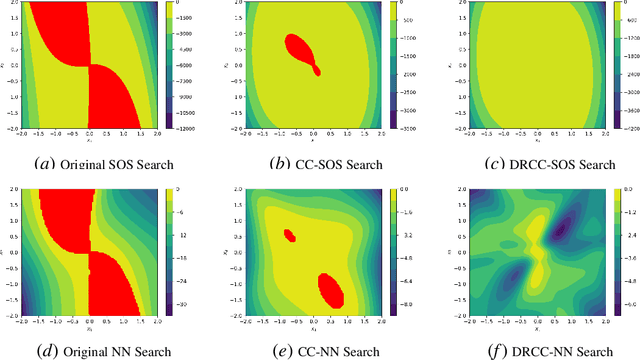
This paper develops methods for proving Lyapunov stability of dynamical systems subject to disturbances with an unknown distribution. We assume only a finite set of disturbance samples is available and that the true online disturbance realization may be drawn from a different distribution than the given samples. We formulate an optimization problem to search for a sum-of-squares (SOS) Lyapunov function and introduce a distributionally robust version of the Lyapunov function derivative constraint. We show that this constraint may be reformulated as several SOS constraints, ensuring that the search for a Lyapunov function remains in the class of SOS polynomial optimization problems. For general systems, we provide a distributionally robust chance-constrained formulation for neural network Lyapunov function search. Simulations demonstrate the validity and efficiency of either formulation on non-linear uncertain dynamical systems.

Safe and Stable Control Synthesis for Uncertain System Models via Distributionally Robust Optimization

This paper considers enforcing safety and stability of dynamical systems in the presence of model uncertainty. Safety and stability constraints may be specified using a control barrier function (CBF) and a control Lyapunov function (CLF), respectively. To take model uncertainty into account, robust and chance formulations of the constraints are commonly considered. However, this requires known error bounds or a known distribution for the model uncertainty, and the resulting formulations may suffer from over-conservatism or over-confidence. In this paper, we assume that only a finite set of model parametric uncertainty samples is available and formulate a distributionally robust chance-constrained program (DRCCP) for control synthesis with CBF safety and CLF stability guarantees. To enable the efficient computation of control inputs during online execution, we provide a reformulation of the DRCCP as a second-order cone program (SOCP). Our formulation is evaluated in an adaptive cruise control example in comparison to 1) a baseline CLF-CBF quadratic programming approach, 2) a robust approach that assumes known error bounds of the system uncertainty, and 3) a chance-constrained approach that assumes a known Gaussian Process distribution of the uncertainty.

Multirobot rendezvous with visibility sensors in nonconvex environments

This paper presents a coordination algorithm for mobile autonomous robots. Relying upon distributed sensing the robots achieve rendezvous, that is, they move to a common location. Each robot is a point mass moving in a nonconvex environment according to an omnidirectional kinematic model. Each robot is equipped with line-of-sight limited-range sensors, i.e., a robot can measure the relative position of any object (robots or environment boundary) if and only if the object is within a given distance and there are no obstacles in-between. The algorithm is designed using the notions of robust visibility, connectivity-preserving constraint sets, and proximity graphs. Simulations illustrate the theoretical results on the correctness of the proposed algorithm, and its performance in asynchronous setups and with sensor measurement and control errors.