Daniel Bruder
UMArm: Untethered, Modular, Wearable, Soft Pneumatic Arm
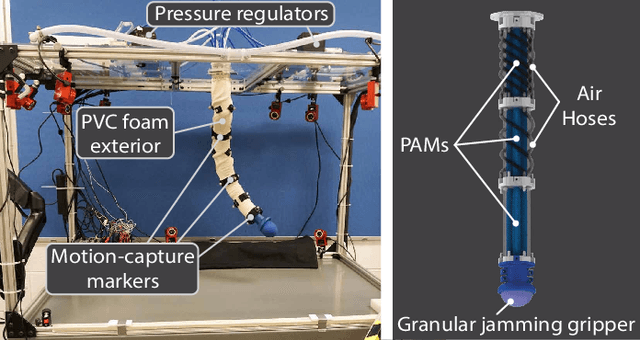
May 16, 2025Abstract:Robotic arms are essential to modern industries, however, their adaptability to unstructured environments remains limited. Soft robotic arms, particularly those actuated pneumatically, offer greater adaptability in unstructured environments and enhanced safety for human-robot interaction. However, current pneumatic soft arms are constrained by limited degrees of freedom, precision, payload capacity, and reliance on bulky external pressure regulators. In this work, a novel pneumatically driven rigid-soft hybrid arm, ``UMArm'', is presented. The shortcomings of pneumatically actuated soft arms are addressed by densely integrating high-force-to-weight-ratio, self-regulated McKibben actuators onto a lightweight rigid spine structure. The modified McKibben actuators incorporate valves and controllers directly inside, eliminating the need for individual pressure lines and external regulators, significantly reducing system weight and complexity. Full untethered operation, high payload capacity, precision, and directionally tunable compliance are achieved by the UMArm. Portability is demonstrated through a wearable assistive arm experiment, and versatility is showcased by reconfiguring the system into an inchworm robot. The results of this work show that the high-degree-of-freedom, external-regulator-free pneumatically driven arm systems like the UMArm possess great potential for real-world unstructured environments.
Koopman Operators in Robot Learning
Aug 08, 2024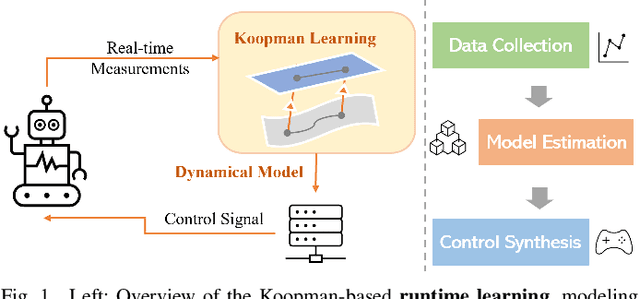
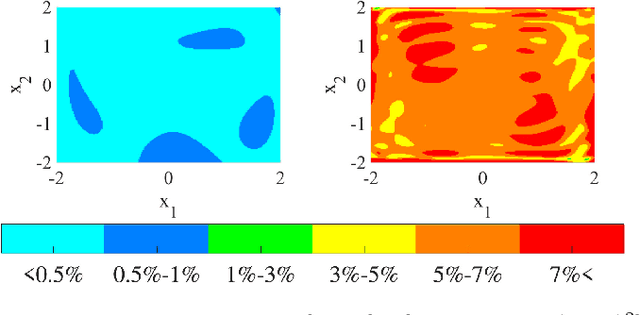
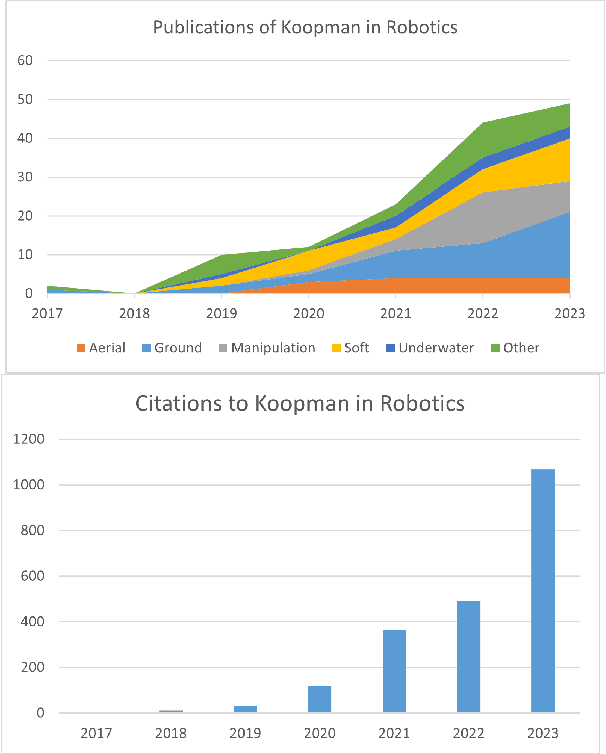
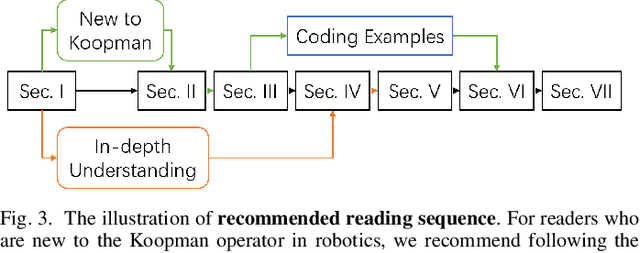
Abstract:Koopman operator theory offers a rigorous treatment of dynamics and has been emerging as a powerful modeling and learning-based control method enabling significant advancements across various domains of robotics. Due to its ability to represent nonlinear dynamics as a linear operator, Koopman theory offers a fresh lens through which to understand and tackle the modeling and control of complex robotic systems. Moreover, it enables incremental updates and is computationally inexpensive making it particularly appealing for real-time applications and online active learning. This review comprehensively presents recent research results on advancing Koopman operator theory across diverse domains of robotics, encompassing aerial, legged, wheeled, underwater, soft, and manipulator robotics. Furthermore, it offers practical tutorials to help new users get started as well as a treatise of more advanced topics leading to an outlook on future directions and open research questions. Taken together, these provide insights into the potential evolution of Koopman theory as applied to the field of robotics.
Advantages of Bilinear Koopman Realizations for the Modeling and Control of Systems with Unknown Dynamics
Oct 26, 2020



Abstract:Nonlinear dynamical systems can be made easier to control by lifting them into the space of observable functions, where their evolution is described by the linear Koopman operator. This paper describes how the Koopman operator can be used to generate approximate linear, bilinear, and nonlinear model realizations from data, and argues in favor of bilinear realizations for characterizing systems with unknown dynamics. Necessary and sufficient conditions for a dynamical system to have a valid linear or bilinear realization over a given set of observable functions are presented and used to show that every control-affine system admits an infinite-dimensional bilinear realization, but does not necessarily admit a linear one. Therefore, approximate bilinear realizations constructed from generic sets of basis functions tend to improve as the number of basis functions increases, whereas approximate linear realizations may not. To demonstrate the advantages of bilinear Koopman realizations for control, a linear, bilinear, and nonlinear Koopman model realization of a simulated robot arm are constructed from data. In a trajectory following task, the bilinear realization exceeds the prediction accuracy of the linear realization and the computational efficiency of the nonlinear realization when incorporated into a model predictive control framework.
Emulating duration and curvature of coral snake anti-predator thrashing behaviors using a soft-robotic platform
Feb 21, 2020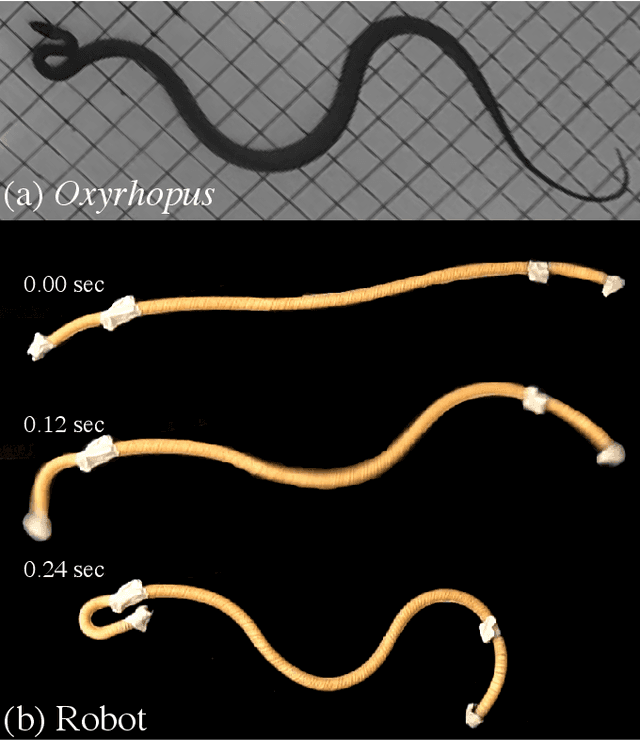
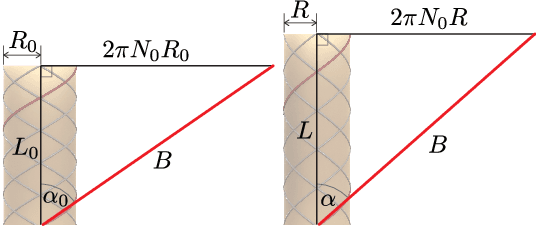
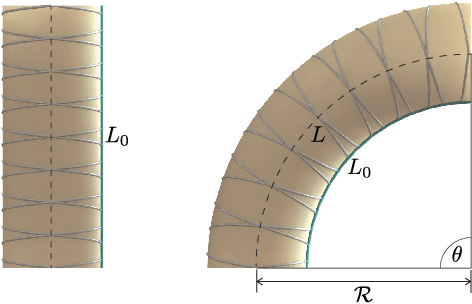
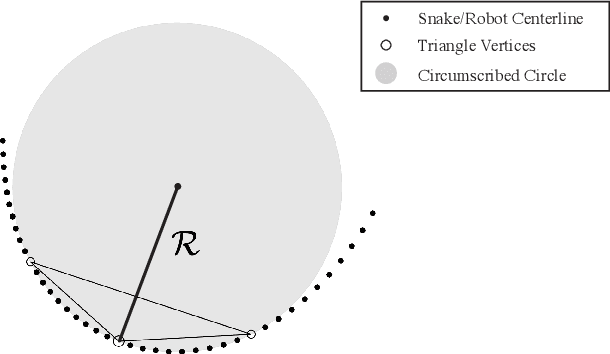
Abstract:This paper presents a soft-robotic platform for exploring the ecological relevance of non-locomotory movements via animal-robot interactions. Coral snakes (genus Micrurus) and their mimics use vigorous, non-locomotory, and arrhythmic thrashing to deter predation. There is variation across snake species in the duration and curvature of anti-predator thrashes, and it is unclear how these aspects of motion interact to contribute to snake survival. In this work, soft robots composed of fiber-reinforced elastomeric enclosures (FREEs) are developed to emulate the anti-predator behaviors of three genera of snake. Curvature and duration of motion are estimated for both live snakes and robots, providing a quantitative assessment of the robots' ability to emulate snake poses. The curvature values of the fabricated soft-robotic head, midsection, and tail segments are found to overlap with those exhibited by live snakes. Soft robot motion durations were less than or equal to those of snakes for all three genera. Additionally, combinations of segments were selected to emulate three specific snake genera with distinct anti-predatory behavior, producing curvature values that aligned well with live snake observations.
Koopman-based Control of a Soft Continuum Manipulator Under Variable Loading Conditions
Feb 04, 2020


Abstract:Controlling soft continuum manipulator arms is difficult due to their infinite degrees of freedom, nonlinear material properties, and large deflections under loading. This paper presents a data-driven approach to identifying soft manipulator models that enables consistent control under variable loading conditions. This is achieved by incorporating loads into a linear Koopman operator model as states and estimating their values online via an observer within the control loop. Using this approach, real-time, fully autonomous control of a pneumatically actuated soft continuum manipulator is achieved. In several trajectory following experiments, this controller is shown to be more accurate and precise than controllers based on models that are unable to explicitly account for loading. The manipulator also successfully performs pick and place of objects with unknown mass, demonstrating the efficacy of this approach in executing real-world manipulation tasks.
Modeling and Control of Soft Robots Using the Koopman Operator and Model Predictive Control
Feb 07, 2019



Abstract:Controlling soft robots with precision is a challenge due in large part to the difficulty of constructing models that are amenable to model-based control design techniques. Koopman Operator Theory offers a way to construct explicit linear dynamical models of soft robots and to control them using established model-based linear control methods. This method is data-driven, yet unlike other data-driven models such as neural networks, it yields an explicit control-oriented linear model rather than just a "black-box" input-output mapping. This work describes this Koopman-based system identification method and its application to model predictive controller design. A model and MPC controller of a pneumatic soft robot arm was constructed via the method, and its performance was evaluated over several trajectory following tasks in the real-world. On all of the tasks, the Koopman-based MPC controller outperformed a benchmark MPC controller based on a linear state-space model of the same system.
Force Generation by Parallel Combinations of Fiber-Reinforced Fluid-Driven Actuators
Oct 26, 2018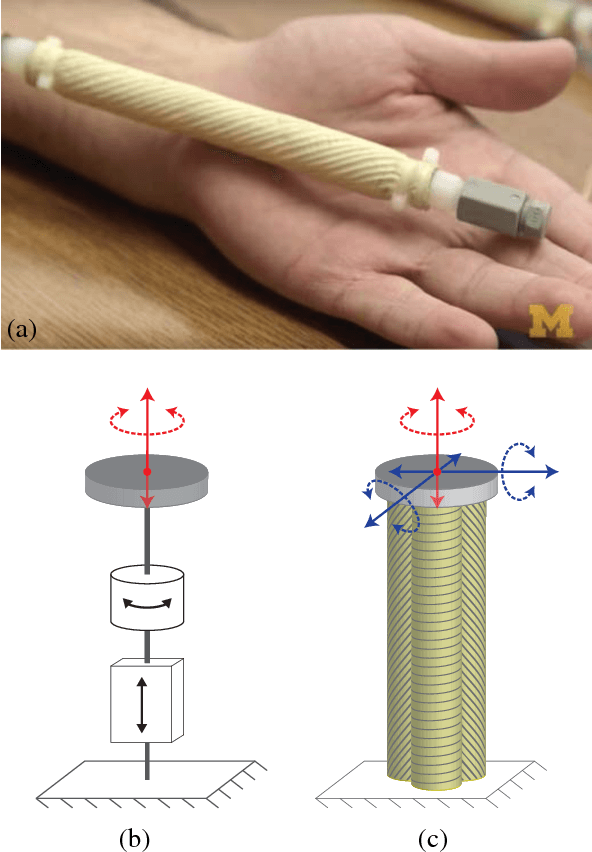


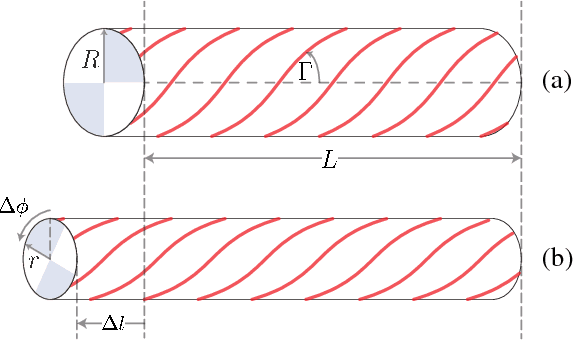
Abstract:The compliant structure of soft robotic systems enables a variety of novel capabilities in comparison to traditional rigid-bodied robots. A subclass of soft fluid-driven actuators known as fiber reinforced elastomeric enclosures (FREEs) is particularly well suited as actuators for these types of systems. FREEs are inherently soft and can impart spatial forces without imposing a rigid structure. Furthermore, they can be configured to produce a large variety of force and moment combinations. In this paper we explore the potential of combining multiple differently configured FREEs in parallel to achieve fully controllable multi-dimensional soft actuation. To this end, we propose a novel methodology to represent and calculate the generalized forces generated by soft actuators as a function of their internal pressure. This methodology relies on the notion of a state dependent fluid Jacobian that yields a linear expression for force. We employ this concept to construct the set of all possible forces that can be generated by a soft system in a given state. This force zonotope can be used to inform the design and control of parallel combinations of soft actuators. The approach is verified experimentally with the parallel combination of three carefully designed actuators constrained to a 2DOF testing rig. The force predictions matched measured values with a root-mean-square error of less than 1.5 N force and 8 x 10^(-3)Nm moment, demonstrating the utility of the presented methodology.
* Published in IEEE Robotics and Automation Letters
Nonlinear System Identification of Soft Robot Dynamics Using Koopman Operator Theory
Oct 15, 2018



Abstract:Soft robots are challenging to model due to their nonlinear behavior. However, their soft bodies make it possible to safely observe their behavior under random control inputs, making them amenable to large-scale data collection and system identification. This paper implements and evaluates a system identification method based on Koopman operator theory. This theory offers a way to represent a nonlinear system as a linear system in the infinite-dimensional space of real-valued functions called observables, enabling models of nonlinear systems to be constructed via linear regression of observed data. The approach does not suffer from some of the shortcomings of other nonlinear system identification methods, which typically require the manual tuning of training parameters and have limited convergence guarantees. A dynamic model of a pneumatic soft robot arm is constructed via this method, and used to predict the behavior of the real system. The total normalized-root-mean-square error (NRMSE) of its predictions over twelve validation trials is lower than that of several other identified models including a neural network, NLARX, nonlinear Hammerstein-Wiener, and linear state space model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge