Koopman Operators in Robot Learning

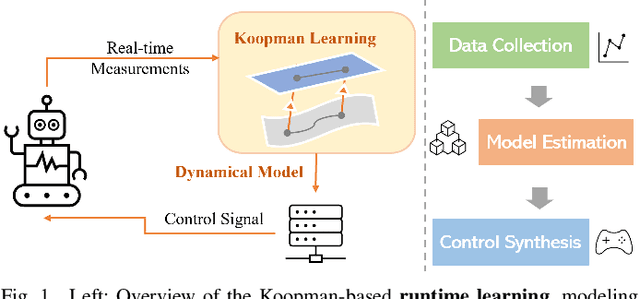
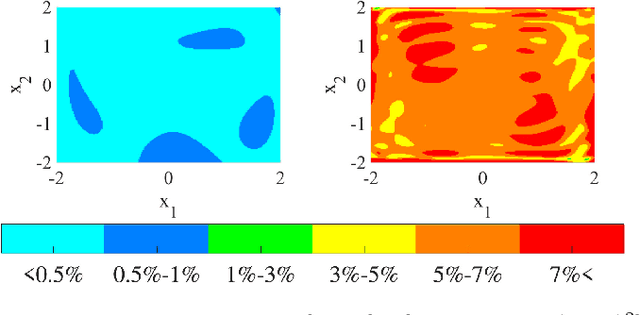
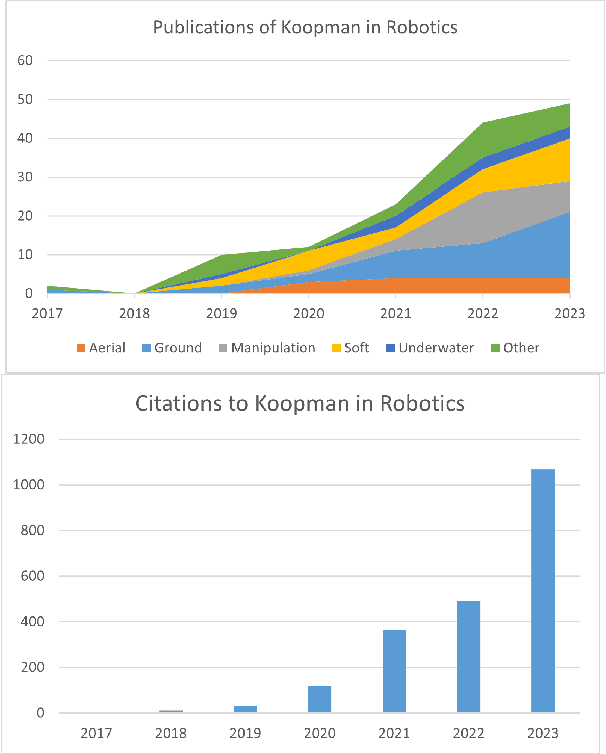
Koopman operator theory offers a rigorous treatment of dynamics and has been emerging as a powerful modeling and learning-based control method enabling significant advancements across various domains of robotics. Due to its ability to represent nonlinear dynamics as a linear operator, Koopman theory offers a fresh lens through which to understand and tackle the modeling and control of complex robotic systems. Moreover, it enables incremental updates and is computationally inexpensive making it particularly appealing for real-time applications and online active learning. This review comprehensively presents recent research results on advancing Koopman operator theory across diverse domains of robotics, encompassing aerial, legged, wheeled, underwater, soft, and manipulator robotics. Furthermore, it offers practical tutorials to help new users get started as well as a treatise of more advanced topics leading to an outlook on future directions and open research questions. Taken together, these provide insights into the potential evolution of Koopman theory as applied to the field of robotics.

Derivative-Based Koopman Operators for Real-Time Control of Robotic Systems

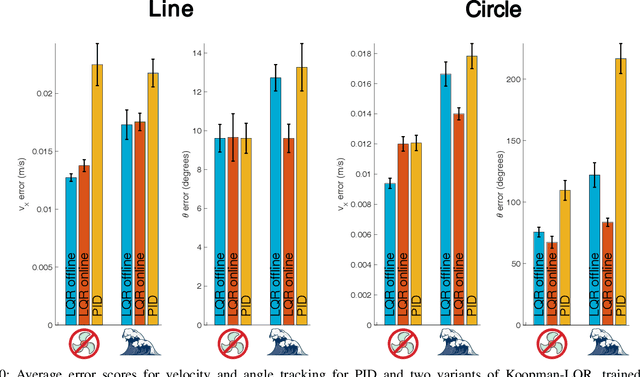
This paper presents a methodology for linear embedding of nonlinear systems that bounds the model error in terms of the prediction horizon and the magnitude of the derivatives of the system states. Using higher-order derivatives of general nonlinear dynamics that need not be known, we construct a Koopman operator-based linear representation and utilize Taylor series accuracy to derive an error bound. The error formula is used to choose the order of derivatives in the basis functions and obtain a data-driven Koopman model using a closed-form expression that can be computed in real time. The Koopman representation of the nonlinear system is then used to synthesize LQR feedback. The efficacy of the embedding approach is demonstrated with simulation and experimental results on the control of a tail-actuated robotic fish. Experimental results show that the proposed data-driven control approach outperforms a tuned PID (Proportional Integral Derivative) controller and that updating the data-driven model online significantly improves performance in the presence of unmodeled fluid disturbance. This paper is complemented with a video: https://youtu.be/9_wx0tdDta0.

Learning Memory-Efficient Stable Linear Dynamical Systems for Prediction and Control

Learning a stable Linear Dynamical System (LDS) from data involves creating models that both minimize reconstruction error and enforce stability of the learned representation. We propose a novel algorithm for learning stable LDSs. Using a recent characterization of stable matrices, we present an optimization method that ensures stability at every step and iteratively improves the reconstruction error using gradient directions derived in this paper. When applied to LDSs with inputs, our approach---in contrast to current methods for learning stable LDSs---updates both the state and control matrices, expanding the solution space and allowing for models with lower reconstruction error. We apply our algorithm in simulations and experiments to a variety of problems, including learning dynamic textures from image sequences and controlling a robotic manipulator. Compared to existing approaches, our proposed method achieves an orders-of-magnitude improvement in reconstruction error and superior results in terms of control performance. In addition, it is provably more memory-efficient, with an O(n^2) space complexity compared to O(n^4) of competing alternatives, thus scaling to higher-dimensional systems when the other methods fail.

Learning Data-Driven Stable Koopman Operators

In this paper, we consider the problem of improving the long-term accuracy of data-driven approximations of Koopman operators, which are infinite-dimensional linear representations of general nonlinear systems, by bounding the eigenvalues of the linear operator. We derive a formula for the global error of general Koopman representations and motivate imposing stability constraints on the data-driven model to improve the approximation of nonlinear systems over a longer horizon. In addition, constraints on admissible basis functions for a stable Koopman operator are presented, as well as conditions for constructing a Lyapunov function for nonlinear systems. The modified linear representation is the nearest \textit{stable} (all eigenvalues are equal or less than 1) matrix solution to a least-squares minimization and bounds the prediction of the system response. We demonstrate the benefit of stable Koopman operators in prediction and control performance using the systems of a pendulum, a hopper, and a quadrotor.

Feedback Synthesis For Underactuated Systems Using Sequential Second-Order Needle Variations

This paper derives nonlinear feedback control synthesis for general control affine systems using second-order actions---the second-order needle variations of optimal control---as the basis for choosing each control response to the current state. A second result of the paper is that the method provably exploits the nonlinear controllability of a system by virtue of an explicit dependence of the second-order needle variation on the Lie bracket between vector fields. As a result, each control decision necessarily decreases the objective when the system is nonlinearly controllable using first-order Lie brackets. Simulation results using a differential drive cart, an underactuated kinematic vehicle in three dimensions, and an underactuated dynamic model of an underwater vehicle demonstrate that the method finds control solutions when the first-order analysis is singular. Lastly, the underactuated dynamic underwater vehicle model demonstrates convergence even in the presence of a velocity field.

Feedback Synthesis for Controllable Underactuated Systems using Sequential Second Order Actions

This paper derives nonlinear feedback control synthesis for general control affine systems using second-order actions---the needle variations of optimal control---as the basis for choosing each control response to the current state. A second result of the paper is that the method provably exploits the nonlinear controllability of a system by virtue of an explicit dependence of the second-order needle variation on the Lie bracket between vector fields. As a result, each control decision necessarily decreases the objective when the system is nonlinearly controllable using first-order Lie brackets. Simulation results using a differential drive cart, an underactuated kinematic vehicle in three dimensions, and an underactuated dynamic model of an underwater vehicle demonstrate that the method finds control solutions when the first-order analysis is singular. Moreover, the simulated examples demonstrate superior convergence when compared to synthesis based on first-order needle variations. Lastly, the underactuated dynamic underwater vehicle model demonstrates the convergence even in the presence of a velocity field.