Flow Matching Ergodic Coverage

Ergodic coverage effectively generates exploratory behaviors for embodied agents by aligning the spatial distribution of the agent's trajectory with a target distribution, where the difference between these two distributions is measured by the ergodic metric. However, existing ergodic coverage methods are constrained by the limited set of ergodic metrics available for control synthesis, fundamentally limiting their performance. In this work, we propose an alternative approach to ergodic coverage based on flow matching, a technique widely used in generative inference for efficient and scalable sampling. We formally derive the flow matching problem for ergodic coverage and show that it is equivalent to a linear quadratic regulator problem with a closed-form solution. Our formulation enables alternative ergodic metrics from generative inference that overcome the limitations of existing ones. These metrics were previously infeasible for control synthesis but can now be supported with no computational overhead. Specifically, flow matching with the Stein variational gradient flow enables control synthesis directly over the score function of the target distribution, improving robustness to the unnormalized distributions; on the other hand, flow matching with the Sinkhorn divergence flow enables an optimal transport-based ergodic metric, improving coverage performance on non-smooth distributions with irregular supports. We validate the improved performance and competitive computational efficiency of our method through comprehensive numerical benchmarks and across different nonlinear dynamics. We further demonstrate the practicality of our method through a series of drawing and erasing tasks on a Franka robot.

Inverse Mixed Strategy Games with Generative Trajectory Models

Game-theoretic models are effective tools for modeling multi-agent interactions, especially when robots need to coordinate with humans. However, applying these models requires inferring their specifications from observed behaviors -- a challenging task known as the inverse game problem. Existing inverse game approaches often struggle to account for behavioral uncertainty and measurement noise, and leverage both offline and online data. To address these limitations, we propose an inverse game method that integrates a generative trajectory model into a differentiable mixed-strategy game framework. By representing the mixed strategy with a conditional variational autoencoder (CVAE), our method can infer high-dimensional, multi-modal behavior distributions from noisy measurements while adapting in real-time to new observations. We extensively evaluate our method in a simulated navigation benchmark, where the observations are generated by an unknown game model. Despite the model mismatch, our method can infer Nash-optimal actions comparable to those of the ground-truth model and the oracle inverse game baseline, even in the presence of uncertain agent objectives and noisy measurements.

Koopman Operators in Robot Learning

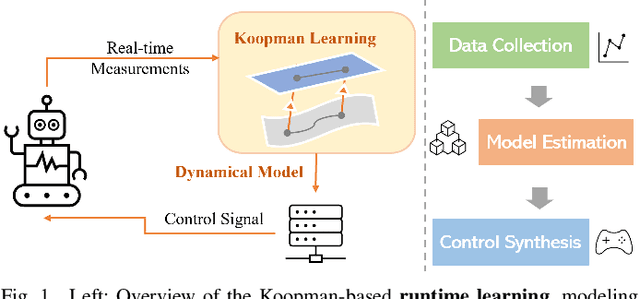
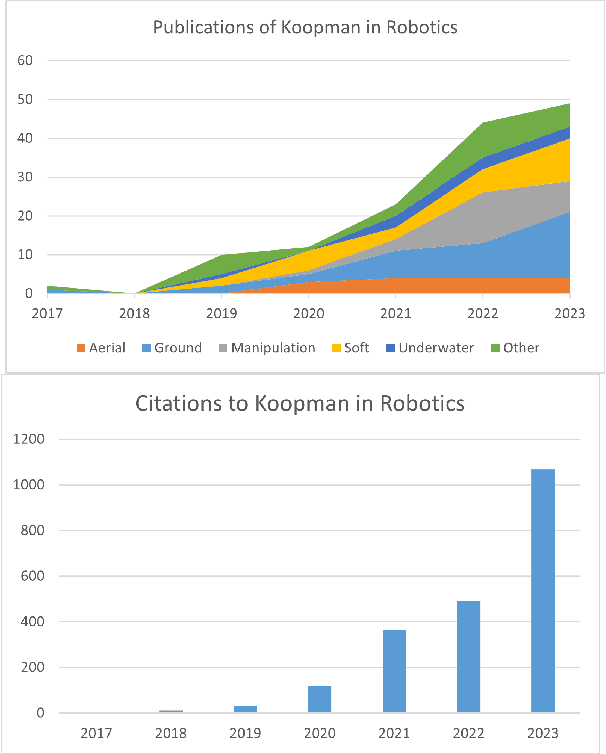
Koopman operator theory offers a rigorous treatment of dynamics and has been emerging as a powerful modeling and learning-based control method enabling significant advancements across various domains of robotics. Due to its ability to represent nonlinear dynamics as a linear operator, Koopman theory offers a fresh lens through which to understand and tackle the modeling and control of complex robotic systems. Moreover, it enables incremental updates and is computationally inexpensive making it particularly appealing for real-time applications and online active learning. This review comprehensively presents recent research results on advancing Koopman operator theory across diverse domains of robotics, encompassing aerial, legged, wheeled, underwater, soft, and manipulator robotics. Furthermore, it offers practical tutorials to help new users get started as well as a treatise of more advanced topics leading to an outlook on future directions and open research questions. Taken together, these provide insights into the potential evolution of Koopman theory as applied to the field of robotics.

Mixed-Strategy Nash Equilibrium for Crowd Navigation

We address the problem of finding mixed-strategy Nash equilibrium for crowd navigation. Mixed-strategy Nash equilibrium provides a rigorous model for the robot to anticipate uncertain yet cooperative human behavior in crowds, but the computation cost is often too high for scalable and real-time decision-making. Here we prove that a simple iterative Bayesian updating scheme converges to the Nash equilibrium of a mixed-strategy social navigation game. Furthermore, we propose a data-driven framework to construct the game by initializing agent strategies as Gaussian processes learned from human datasets. Based on the proposed mixed-strategy Nash equilibrium model, we develop a sampling-based crowd navigation framework that can be integrated into existing navigation methods and runs in real-time on a laptop CPU. We evaluate our framework in both simulated environments and real-world human datasets in unstructured environments. Our framework consistently outperforms both non-learning and learning-based methods on both safety and navigation efficiency and reaches human-level crowd navigation performance on top of a meta-planner.

Fast Ergodic Search with Kernel Functions

Ergodic search enables optimal exploration of an information distribution while guaranteeing the asymptotic coverage of the search space. However, current methods typically have exponential computation complexity in the search space dimension and are restricted to Euclidean space. We introduce a computationally efficient ergodic search method. Our contributions are two-fold. First, we develop a kernel-based ergodic metric and generalize it from Euclidean space to Lie groups. We formally prove the proposed metric is consistent with the standard ergodic metric while guaranteeing linear complexity in the search space dimension. Secondly, we derive the first-order optimality condition of the kernel ergodic metric for nonlinear systems, which enables efficient trajectory optimization. Comprehensive numerical benchmarks show that the proposed method is at least two orders of magnitude faster than the state-of-the-art algorithm. Finally, we demonstrate the proposed algorithm with a peg-in-hole insertion task. We formulate the problem as a coverage task in the space of SE(3) and use a 30-second-long human demonstration as the prior distribution for ergodic coverage. Ergodicity guarantees the asymptotic solution of the peg-in-hole problem so long as the solution resides within the prior information distribution, which is seen in the 100\% success rate.

Human Robot Pacing Mismatch

A widely accepted explanation for robots planning overcautious or overaggressive trajectories alongside human is that the crowd density exceeds a threshold such that all feasible trajectories are considered unsafe -- the freezing robot problem. However, even with low crowd density, the robot's navigation performance could still drop drastically when in close proximity to human. In this work, we argue that a broader cause of suboptimal navigation performance near human is due to the robot's misjudgement for the human's willingness (flexibility) to share space with others, particularly when the robot assumes the human's flexibility holds constant during interaction, a phenomenon of what we call human robot pacing mismatch. We show that the necessary condition for solving pacing mismatch is to model the evolution of both the robot and the human's flexibility during decision making, a strategy called distribution space modeling. We demonstrate the advantage of distribution space coupling through an anecdotal case study and discuss the future directions of solving human robot pacing mismatch.

Decentralization and Acceleration Enables Large-Scale Bundle Adjustment

Scaling to arbitrarily large bundle adjustment problems requires data and compute to be distributed across multiple devices. Centralized methods in prior works are only able to solve small or medium size problems due to overhead in computation and communication. In this paper, we present a fully decentralized method that alleviates computation and communication bottlenecks to solve arbitrarily large bundle adjustment problems. We achieve this by reformulating the reprojection error and deriving a novel surrogate function that decouples optimization variables from different devices. This function makes it possible to use majorization minimization techniques and reduces bundle adjustment to independent optimization subproblems that can be solved in parallel. We further apply Nesterov's acceleration and adaptive restart to improve convergence while maintaining its theoretical guarantees. Despite limited peer-to-peer communication, our method has provable convergence to first-order critical points under mild conditions. On extensive benchmarks with public datasets, our method converges much faster than decentralized baselines with similar memory usage and communication load. Compared to centralized baselines using a single device, our method, while being decentralized, yields more accurate solutions with significant speedups of up to 953.7x over Ceres and 174.6x over DeepLM. Code: https://github.com/facebookresearch/DABA.

Scale-Invariant Specifications for Human-Swarm Systems

We present a method for controlling a swarm using its spectral decomposition -- that is, by describing the set of trajectories of a swarm in terms of a spatial distribution throughout the operational domain -- guaranteeing scale invariance with respect to the number of agents both for computation and for the operator tasked with controlling the swarm. We use ergodic control, decentralized across the network, for implementation. In the DARPA OFFSET program field setting, we test this interface design for the operator using the STOMP interface -- the same interface used by Raytheon BBN throughout the duration of the OFFSET program. In these tests, we demonstrate that our approach is scale-invariant -- the user specification does not depend on the number of agents; it is persistent -- the specification remains active until the user specifies a new command; and it is real-time -- the user can interact with and interrupt the swarm at any time. Moreover, we show that the spectral/ergodic specification of swarm behavior degrades gracefully as the number of agents goes down, enabling the operator to maintain the same approach as agents become disabled or are added to the network. We demonstrate the scale-invariance and dynamic response of our system in a field relevant simulator on a variety of tactical scenarios with up to 50 agents. We also demonstrate the dynamic response of our system in the field with a smaller team of agents. Lastly, we make the code for our system available.

Scale-Invariant Fast Functional Registration

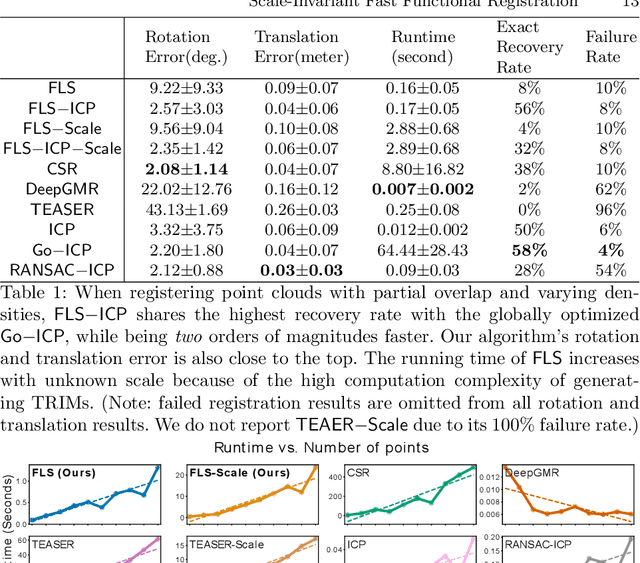
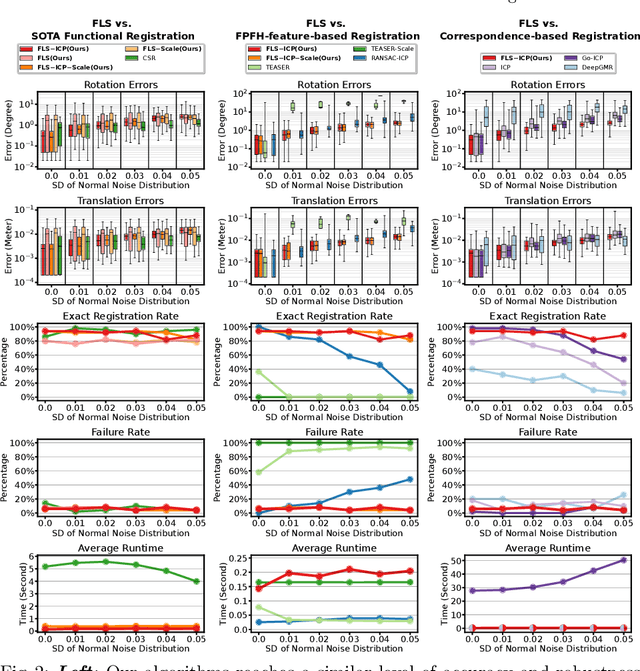
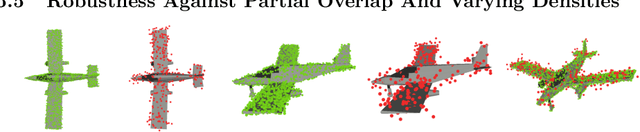
Functional registration algorithms represent point clouds as functions (e.g. spacial occupancy field) avoiding unreliable correspondence estimation in conventional least-squares registration algorithms. However, existing functional registration algorithms are computationally expensive. Furthermore, the capability of registration with unknown scale is necessary in tasks such as CAD model-based object localization, yet no such support exists in functional registration. In this work, we propose a scale-invariant, linear time complexity functional registration algorithm. We achieve linear time complexity through an efficient approximation of L2-distance between functions using orthonormal basis functions. The use of orthonormal basis functions leads to a formulation that is compatible with least-squares registration. Benefited from the least-square formulation, we use the theory of translation-rotation-invariant measurement to decouple scale estimation and therefore achieve scale-invariant registration. We evaluate the proposed algorithm, named FLS (functional least-squares), on standard 3D registration benchmarks, showing FLS is an order of magnitude faster than state-of-the-art functional registration algorithm without compromising accuracy and robustness. FLS also outperforms state-of-the-art correspondence-based least-squares registration algorithm on accuracy and robustness, with known and unknown scale. Finally, we demonstrate applying FLS to register point clouds with varying densities and partial overlaps, point clouds from different objects within the same category, and point clouds from real world objects with noisy RGB-D measurements.

Majorization Minimization Methods for Distributed Pose Graph Optimization

We consider the problem of distributed pose graph optimization (PGO) that has important applications in multi-robot simultaneous localization and mapping (SLAM). We propose the majorization minimization (MM) method for distributed PGO ($\mathsf{MM\!\!-\!\!PGO}$) that applies to a broad class of robust loss kernels. The $\mathsf{MM\!\!-\!\!PGO}$ method is guaranteed to converge to first-order critical points under mild conditions. Furthermore, noting that the $\mathsf{MM\!\!-\!\!PGO}$ method is reminiscent of proximal methods, we leverage Nesterov's method and adopt adaptive restarts to accelerate convergence. The resulting accelerated MM methods for distributed PGO -- both with a master node in the network ($\mathsf{AMM\!\!-\!\!PGO}^*$) and without ($\mathsf{AMM\!\!-\!\!PGO}^{\#}$) -- have faster convergence in contrast to the $\mathsf{MM\!\!-\!\!PGO}$ method without sacrificing theoretical guarantees. In particular, the $\mathsf{AMM\!\!-\!\!PGO}^{\#}$ method, which needs no master node and is fully decentralized, features a novel adaptive restart scheme and has a rate of convergence comparable to that of the $\mathsf{AMM\!\!-\!\!PGO}^*$ method using a master node to aggregate information from all the other nodes. The efficacy of this work is validated through extensive applications to 2D and 3D SLAM benchmark datasets and comprehensive comparisons against existing state-of-the-art methods, indicating that our MM methods converge faster and result in better solutions to distributed PGO.