Sparsh: Self-supervised touch representations for vision-based tactile sensing

In this work, we introduce general purpose touch representations for the increasingly accessible class of vision-based tactile sensors. Such sensors have led to many recent advances in robot manipulation as they markedly complement vision, yet solutions today often rely on task and sensor specific handcrafted perception models. Collecting real data at scale with task centric ground truth labels, like contact forces and slip, is a challenge further compounded by sensors of various form factor differing in aspects like lighting and gel markings. To tackle this we turn to self-supervised learning (SSL) that has demonstrated remarkable performance in computer vision. We present Sparsh, a family of SSL models that can support various vision-based tactile sensors, alleviating the need for custom labels through pre-training on 460k+ tactile images with masking and self-distillation in pixel and latent spaces. We also build TacBench, to facilitate standardized benchmarking across sensors and models, comprising of six tasks ranging from comprehending tactile properties to enabling physical perception and manipulation planning. In evaluations, we find that SSL pre-training for touch representation outperforms task and sensor-specific end-to-end training by 95.1% on average over TacBench, and Sparsh (DINO) and Sparsh (IJEPA) are the most competitive, indicating the merits of learning in latent space for tactile images. Project page: https://sparsh-ssl.github.io/

Neural feels with neural fields: Visuo-tactile perception for in-hand manipulation

To achieve human-level dexterity, robots must infer spatial awareness from multimodal sensing to reason over contact interactions. During in-hand manipulation of novel objects, such spatial awareness involves estimating the object's pose and shape. The status quo for in-hand perception primarily employs vision, and restricts to tracking a priori known objects. Moreover, visual occlusion of objects in-hand is imminent during manipulation, preventing current systems to push beyond tasks without occlusion. We combine vision and touch sensing on a multi-fingered hand to estimate an object's pose and shape during in-hand manipulation. Our method, NeuralFeels, encodes object geometry by learning a neural field online and jointly tracks it by optimizing a pose graph problem. We study multimodal in-hand perception in simulation and the real-world, interacting with different objects via a proprioception-driven policy. Our experiments show final reconstruction F-scores of $81$% and average pose drifts of $4.7\,\text{mm}$, further reduced to $2.3\,\text{mm}$ with known CAD models. Additionally, we observe that under heavy visual occlusion we can achieve up to $94$% improvements in tracking compared to vision-only methods. Our results demonstrate that touch, at the very least, refines and, at the very best, disambiguates visual estimates during in-hand manipulation. We release our evaluation dataset of 70 experiments, FeelSight, as a step towards benchmarking in this domain. Our neural representation driven by multimodal sensing can serve as a perception backbone towards advancing robot dexterity. Videos can be found on our project website https://suddhu.github.io/neural-feels/

Decentralization and Acceleration Enables Large-Scale Bundle Adjustment

Scaling to arbitrarily large bundle adjustment problems requires data and compute to be distributed across multiple devices. Centralized methods in prior works are only able to solve small or medium size problems due to overhead in computation and communication. In this paper, we present a fully decentralized method that alleviates computation and communication bottlenecks to solve arbitrarily large bundle adjustment problems. We achieve this by reformulating the reprojection error and deriving a novel surrogate function that decouples optimization variables from different devices. This function makes it possible to use majorization minimization techniques and reduces bundle adjustment to independent optimization subproblems that can be solved in parallel. We further apply Nesterov's acceleration and adaptive restart to improve convergence while maintaining its theoretical guarantees. Despite limited peer-to-peer communication, our method has provable convergence to first-order critical points under mild conditions. On extensive benchmarks with public datasets, our method converges much faster than decentralized baselines with similar memory usage and communication load. Compared to centralized baselines using a single device, our method, while being decentralized, yields more accurate solutions with significant speedups of up to 953.7x over Ceres and 174.6x over DeepLM. Code: https://github.com/facebookresearch/DABA.

Theseus: A Library for Differentiable Nonlinear Optimization

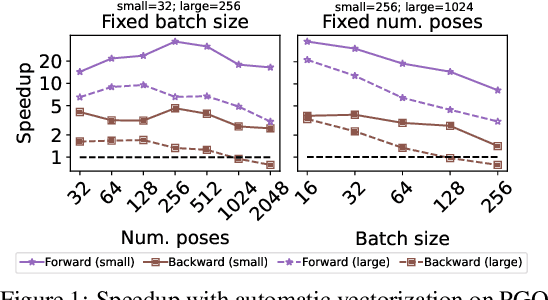
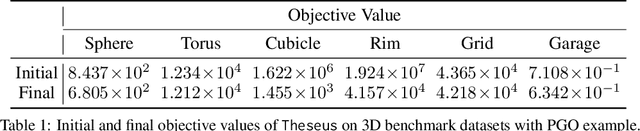
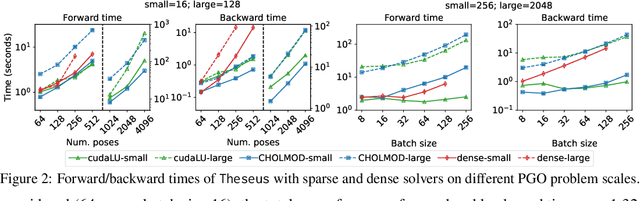
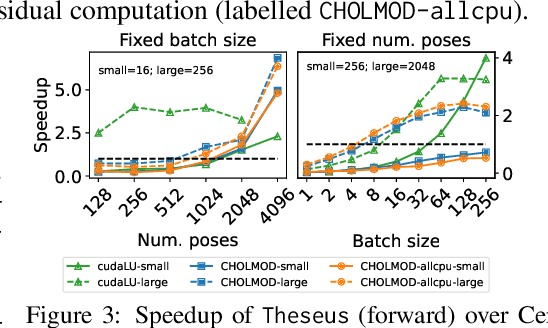
We present Theseus, an efficient application-agnostic open source library for differentiable nonlinear least squares (DNLS) optimization built on PyTorch, providing a common framework for end-to-end structured learning in robotics and vision. Existing DNLS implementations are application specific and do not always incorporate many ingredients important for efficiency. Theseus is application-agnostic, as we illustrate with several example applications that are built using the same underlying differentiable components, such as second-order optimizers, standard costs functions, and Lie groups. For efficiency, Theseus incorporates support for sparse solvers, automatic vectorization, batching, GPU acceleration, and gradient computation with implicit differentiation and direct loss minimization. We do extensive performance evaluation in a set of applications, demonstrating significant efficiency gains and better scalability when these features are incorporated. Project page: https://sites.google.com/view/theseus-ai

Majorization Minimization Methods for Distributed Pose Graph Optimization

We consider the problem of distributed pose graph optimization (PGO) that has important applications in multi-robot simultaneous localization and mapping (SLAM). We propose the majorization minimization (MM) method for distributed PGO ($\mathsf{MM\!\!-\!\!PGO}$) that applies to a broad class of robust loss kernels. The $\mathsf{MM\!\!-\!\!PGO}$ method is guaranteed to converge to first-order critical points under mild conditions. Furthermore, noting that the $\mathsf{MM\!\!-\!\!PGO}$ method is reminiscent of proximal methods, we leverage Nesterov's method and adopt adaptive restarts to accelerate convergence. The resulting accelerated MM methods for distributed PGO -- both with a master node in the network ($\mathsf{AMM\!\!-\!\!PGO}^*$) and without ($\mathsf{AMM\!\!-\!\!PGO}^{\#}$) -- have faster convergence in contrast to the $\mathsf{MM\!\!-\!\!PGO}$ method without sacrificing theoretical guarantees. In particular, the $\mathsf{AMM\!\!-\!\!PGO}^{\#}$ method, which needs no master node and is fully decentralized, features a novel adaptive restart scheme and has a rate of convergence comparable to that of the $\mathsf{AMM\!\!-\!\!PGO}^*$ method using a master node to aggregate information from all the other nodes. The efficacy of this work is validated through extensive applications to 2D and 3D SLAM benchmark datasets and comprehensive comparisons against existing state-of-the-art methods, indicating that our MM methods converge faster and result in better solutions to distributed PGO.

Revitalizing Optimization for 3D Human Pose and Shape Estimation: A Sparse Constrained Formulation

We propose a novel sparse constrained formulation and from it derive a real-time optimization method for 3D human pose and shape estimation. Our optimization method is orders of magnitude faster (avg. 4 ms convergence) than existing optimization methods, while being mathematically equivalent to their dense unconstrained formulation. We achieve this by exploiting the underlying sparsity and constraints of our formulation to efficiently compute the Gauss-Newton direction. We show that this computation scales linearly with the number of joints of a complex 3D human model, in contrast to prior work where it scales cubically due to their dense unconstrained formulation. Based on our optimization method, we present a real-time motion capture framework that estimates 3D human poses and shapes from a single image at over 30 FPS. In benchmarks against state-of-the-art methods on multiple public datasets, our frame-work outperforms other optimization methods and achieves competitive accuracy against regression methods.

Generalized Proximal Methods for Pose Graph Optimization

In this paper, we generalize proximal methods that were originally designed for convex optimization on normed vector space to non-convex pose graph optimization (PGO) on special Euclidean groups, and show that our proposed generalized proximal methods for PGO converge to first-order critical points. Furthermore, we propose methods that significantly accelerate the rates of convergence almost without loss of any theoretical guarantees. In addition, our proposed methods can be easily distributed and parallelized with no compromise of efficiency. The efficacy of this work is validated through implementation on simultaneous localization and mapping (SLAM) and distributed 3D sensor network localization, which indicate that our proposed methods are a lot faster than existing techniques to converge to sufficient accuracy for practical use.

CPL-SLAM: Efficient and Certifiably Correct Planar Graph-Based SLAM Using the Complex Number Representation

In this paper, we consider the problem of planar graph-based simultaneous localization and mapping (SLAM) that involves both poses of the autonomous agent and positions of observed landmarks. We present CPL-SLAM, an efficient and certifiably correct algorithm to solve planar graph-based SLAM using the complex number representation. We formulate and simplify planar graph-based SLAM as the maximum likelihood estimation (MLE) on the product of unit complex numbers, and relax this nonconvex quadratic complex optimization problem to convex complex semidefinite programming (SDP). Furthermore, we simplify the corresponding complex semidefinite programming to Riemannian staircase optimization (RSO) on the complex oblique manifold that can be solved with the Riemannian trust region (RTR) method. In addition, we prove that the SDP relaxation and RSO simplification are tight as long as the noise magnitude is below a certain threshold. The efficacy of this work is validated through applications of CPL-SLAM and comparisons with existing state-of-the-art methods on planar graph-based SLAM, which indicates that our proposed algorithm is capable of solving planar graph-based SLAM certifiably, and is more efficient in numerical computation and more robust to measurement noise than existing state-of-the-art methods. The C++ code for CPL-SLAM is available at https://github.com/MurpheyLab/CPL-SLAM.

Majorization Minimization Methods to Distributed Pose Graph Optimization with Convergence Guarantees

In this paper, we consider the problem of distributed pose graph optimization (PGO) that has extensive applications in multi-robot simultaneous localization and mapping (SLAM). We propose majorization minimization methods to distributed PGO and show that our proposed methods are guaranteed to converge to first-order critical points under mild conditions. Furthermore, since our proposed methods rely a proximal operator of distributed PGO, the convergence rate can be significantly accelerated with Nesterov's method, and more importantly, the acceleration induces no compromise of theoretical guarantees. In addition, we also present accelerated majorization minimization methods to the distributed chordal initialization that have a quadratic convergence, which can be used to compute an initial guess for distributed PGO. The efficacy of this work is validated through applications on a number of 2D and 3D SLAM datasets and comparisons with existing state-of-the-art methods, which indicates that our proposed methods have faster convergence and result in better solutions to distributed PGO.

Efficient Computation of Higher-Order Variational Integrators in Robotic Simulation and Trajectory Optimization

This paper addresses the problem of efficiently computing higher-order variational integrators in simulation and trajectory optimization of mechanical systems as those often found in robotic applications. We develop $O(n)$ algorithms to evaluate the discrete Euler-Lagrange (DEL) equations and compute the Newton direction for solving the DEL equations, which results in linear-time variational integrators of arbitrarily high order. To our knowledge, no linear-time higher-order variational or even implicit integrators have been developed before. Moreover, an $O(n^2)$ algorithm to linearize the DEL equations is presented, which is useful for trajectory optimization. These proposed algorithms eliminate the bottleneck of implementing higher-order variational integrators in simulation and trajectory optimization of complex robotic systems. The efficacy of this paper is validated through comparison with existing methods, and implementation on various robotic systems---including trajectory optimization of the Spring Flamingo robot, the LittleDog robot and the Atlas robot. The results illustrate that the same integrator can be used for simulation and trajectory optimization in robotics, preserving mechanical properties while achieving good scalability and accuracy.