Decentralization and Acceleration Enables Large-Scale Bundle Adjustment

Scaling to arbitrarily large bundle adjustment problems requires data and compute to be distributed across multiple devices. Centralized methods in prior works are only able to solve small or medium size problems due to overhead in computation and communication. In this paper, we present a fully decentralized method that alleviates computation and communication bottlenecks to solve arbitrarily large bundle adjustment problems. We achieve this by reformulating the reprojection error and deriving a novel surrogate function that decouples optimization variables from different devices. This function makes it possible to use majorization minimization techniques and reduces bundle adjustment to independent optimization subproblems that can be solved in parallel. We further apply Nesterov's acceleration and adaptive restart to improve convergence while maintaining its theoretical guarantees. Despite limited peer-to-peer communication, our method has provable convergence to first-order critical points under mild conditions. On extensive benchmarks with public datasets, our method converges much faster than decentralized baselines with similar memory usage and communication load. Compared to centralized baselines using a single device, our method, while being decentralized, yields more accurate solutions with significant speedups of up to 953.7x over Ceres and 174.6x over DeepLM. Code: https://github.com/facebookresearch/DABA.

Theseus: A Library for Differentiable Nonlinear Optimization

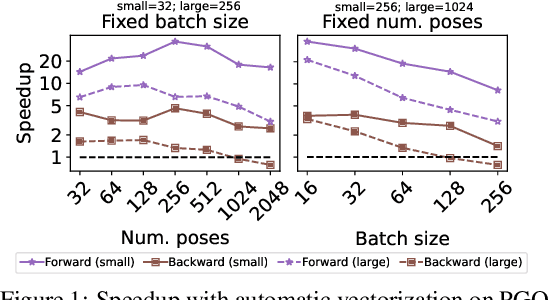
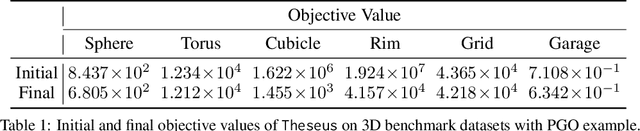
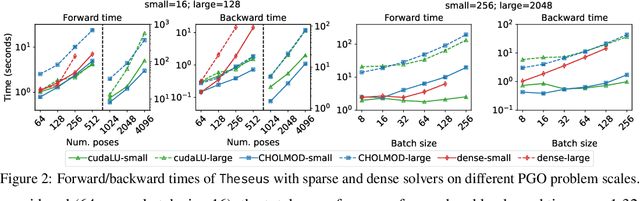
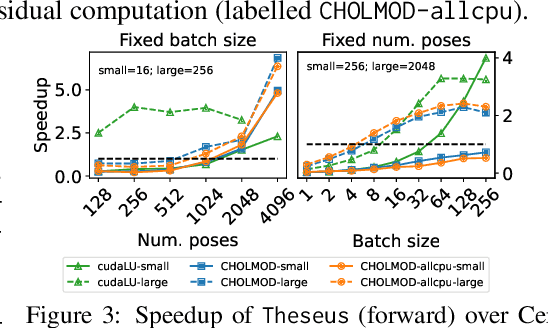
We present Theseus, an efficient application-agnostic open source library for differentiable nonlinear least squares (DNLS) optimization built on PyTorch, providing a common framework for end-to-end structured learning in robotics and vision. Existing DNLS implementations are application specific and do not always incorporate many ingredients important for efficiency. Theseus is application-agnostic, as we illustrate with several example applications that are built using the same underlying differentiable components, such as second-order optimizers, standard costs functions, and Lie groups. For efficiency, Theseus incorporates support for sparse solvers, automatic vectorization, batching, GPU acceleration, and gradient computation with implicit differentiation and direct loss minimization. We do extensive performance evaluation in a set of applications, demonstrating significant efficiency gains and better scalability when these features are incorporated. Project page: https://sites.google.com/view/theseus-ai