Sparsh: Self-supervised touch representations for vision-based tactile sensing

In this work, we introduce general purpose touch representations for the increasingly accessible class of vision-based tactile sensors. Such sensors have led to many recent advances in robot manipulation as they markedly complement vision, yet solutions today often rely on task and sensor specific handcrafted perception models. Collecting real data at scale with task centric ground truth labels, like contact forces and slip, is a challenge further compounded by sensors of various form factor differing in aspects like lighting and gel markings. To tackle this we turn to self-supervised learning (SSL) that has demonstrated remarkable performance in computer vision. We present Sparsh, a family of SSL models that can support various vision-based tactile sensors, alleviating the need for custom labels through pre-training on 460k+ tactile images with masking and self-distillation in pixel and latent spaces. We also build TacBench, to facilitate standardized benchmarking across sensors and models, comprising of six tasks ranging from comprehending tactile properties to enabling physical perception and manipulation planning. In evaluations, we find that SSL pre-training for touch representation outperforms task and sensor-specific end-to-end training by 95.1% on average over TacBench, and Sparsh (DINO) and Sparsh (IJEPA) are the most competitive, indicating the merits of learning in latent space for tactile images. Project page: https://sparsh-ssl.github.io/

Sampling and estimation on manifolds using the Langevin diffusion

Error bounds are derived for sampling and estimation using a discretization of an intrinsically defined Langevin diffusion with invariant measure $d\mu_\phi \propto e^{-\phi} \mathrm{dvol}_g $ on a compact Riemannian manifold. Two estimators of linear functionals of $\mu_\phi $ based on the discretized Markov process are considered: a time-averaging estimator based on a single trajectory and an ensemble-averaging estimator based on multiple independent trajectories. Imposing no restrictions beyond a nominal level of smoothness on $\phi$, first-order error bounds, in discretization step size, on the bias and variances of both estimators are derived. The order of error matches the optimal rate in Euclidean and flat spaces, and leads to a first-order bound on distance between the invariant measure $\mu_\phi$ and a stationary measure of the discretized Markov process. Generality of the proof techniques, which exploit links between two partial differential equations and the semigroup of operators corresponding to the Langevin diffusion, renders them amenable for the study of a more general class of sampling algorithms related to the Langevin diffusion. Conditions for extending analysis to the case of non-compact manifolds are discussed. Numerical illustrations with distributions, log-concave and otherwise, on the manifolds of positive and negative curvature elucidate on the derived bounds and demonstrate practical utility of the sampling algorithm.

Compositional Scalable Object SLAM

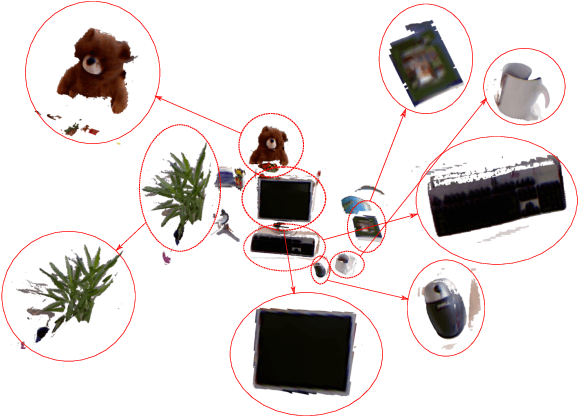
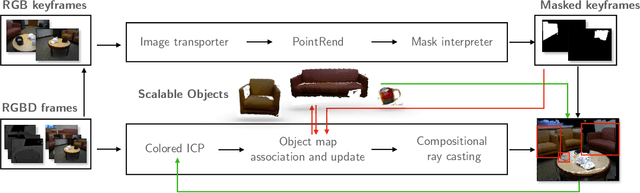
We present a fast, scalable, and accurate Simultaneous Localization and Mapping (SLAM) system that represents indoor scenes as a graph of objects. Leveraging the observation that artificial environments are structured and occupied by recognizable objects, we show that a compositional scalable object mapping formulation is amenable to a robust SLAM solution for drift-free large scale indoor reconstruction. To achieve this, we propose a novel semantically assisted data association strategy that obtains unambiguous persistent object landmarks, and a 2.5D compositional rendering method that enables reliable frame-to-model RGB-D tracking. Consequently, we deliver an optimized online implementation that can run at near frame rate with a single graphics card, and provide a comprehensive evaluation against state of the art baselines. An open source implementation will be provided at https://placeholder.