Probabilistic size-and-shape functional mixed models

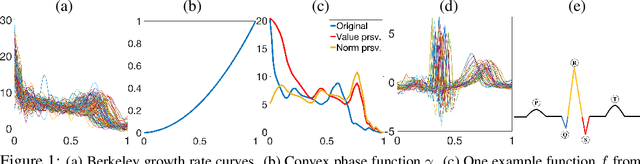
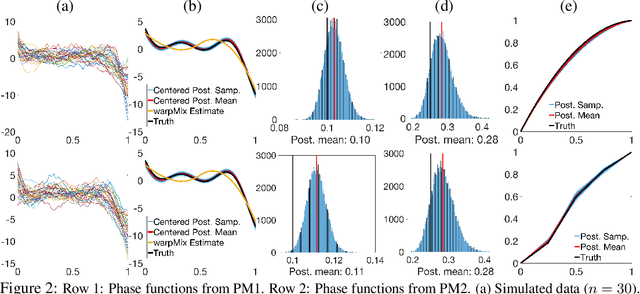
The reliable recovery and uncertainty quantification of a fixed effect function $\mu$ in a functional mixed model, for modelling population- and object-level variability in noisily observed functional data, is a notoriously challenging task: variations along the $x$ and $y$ axes are confounded with additive measurement error, and cannot in general be disentangled. The question then as to what properties of $\mu$ may be reliably recovered becomes important. We demonstrate that it is possible to recover the size-and-shape of a square-integrable $\mu$ under a Bayesian functional mixed model. The size-and-shape of $\mu$ is a geometric property invariant to a family of space-time unitary transformations, viewed as rotations of the Hilbert space, that jointly transform the $x$ and $y$ axes. A random object-level unitary transformation then captures size-and-shape \emph{preserving} deviations of $\mu$ from an individual function, while a random linear term and measurement error capture size-and-shape \emph{altering} deviations. The model is regularized by appropriate priors on the unitary transformations, posterior summaries of which may then be suitably interpreted as optimal data-driven rotations of a fixed orthonormal basis for the Hilbert space. Our numerical experiments demonstrate utility of the proposed model, and superiority over the current state-of-the-art.

Sampling and estimation on manifolds using the Langevin diffusion

Error bounds are derived for sampling and estimation using a discretization of an intrinsically defined Langevin diffusion with invariant measure $d\mu_\phi \propto e^{-\phi} \mathrm{dvol}_g $ on a compact Riemannian manifold. Two estimators of linear functionals of $\mu_\phi $ based on the discretized Markov process are considered: a time-averaging estimator based on a single trajectory and an ensemble-averaging estimator based on multiple independent trajectories. Imposing no restrictions beyond a nominal level of smoothness on $\phi$, first-order error bounds, in discretization step size, on the bias and variances of both estimators are derived. The order of error matches the optimal rate in Euclidean and flat spaces, and leads to a first-order bound on distance between the invariant measure $\mu_\phi$ and a stationary measure of the discretized Markov process. Generality of the proof techniques, which exploit links between two partial differential equations and the semigroup of operators corresponding to the Langevin diffusion, renders them amenable for the study of a more general class of sampling algorithms related to the Langevin diffusion. Conditions for extending analysis to the case of non-compact manifolds are discussed. Numerical illustrations with distributions, log-concave and otherwise, on the manifolds of positive and negative curvature elucidate on the derived bounds and demonstrate practical utility of the sampling algorithm.

Shape And Structure Preserving Differential Privacy

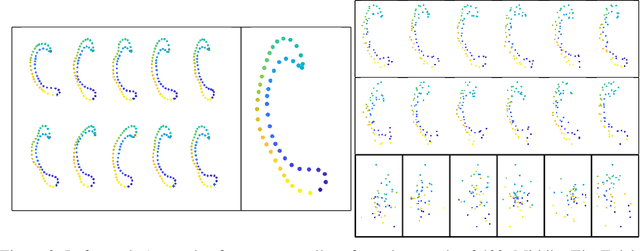
It is common for data structures such as images and shapes of 2D objects to be represented as points on a manifold. The utility of a mechanism to produce sanitized differentially private estimates from such data is intimately linked to how compatible it is with the underlying structure and geometry of the space. In particular, as recently shown, utility of the Laplace mechanism on a positively curved manifold, such as Kendall's 2D shape space, is significantly influences by the curvature. Focusing on the problem of sanitizing the Fr\'echet mean of a sample of points on a manifold, we exploit the characterisation of the mean as the minimizer of an objective function comprised of the sum of squared distances and develop a K-norm gradient mechanism on Riemannian manifolds that favors values that produce gradients close to the the zero of the objective function. For the case of positively curved manifolds, we describe how using the gradient of the squared distance function offers better control over sensitivity than the Laplace mechanism, and demonstrate this numerically on a dataset of shapes of corpus callosa. Further illustrations of the mechanism's utility on a sphere and the manifold of symmetric positive definite matrices are also presented.

Differential Privacy Over Riemannian Manifolds

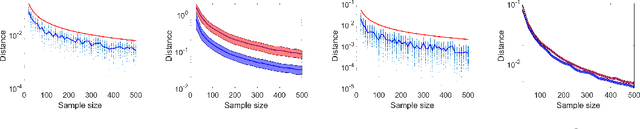
In this work we consider the problem of releasing a differentially private statistical summary that resides on a Riemannian manifold. We present an extension of the Laplace or K-norm mechanism that utilizes intrinsic distances and volumes on the manifold. We also consider in detail the specific case where the summary is the Fr\'echet mean of data residing on a manifold. We demonstrate that our mechanism is rate optimal and depends only on the dimension of the manifold, not on the dimension of any ambient space, while also showing how ignoring the manifold structure can decrease the utility of the sanitized summary. We illustrate our framework in two examples of particular interest in statistics: the space of symmetric positive definite matrices, which is used for covariance matrices, and the sphere, which can be used as a space for modeling discrete distributions.

A diffusion approach to Stein's method on Riemannian manifolds

We detail an approach to develop Stein's method for bounding integral metrics on probability measures defined on a Riemannian manifold $\mathbf{M}$. Our approach exploits the relationship between the generator of a diffusion on $\mathbf{M}$ with target invariant measure and its characterising Stein operator. We consider a pair of such diffusions with different starting points, and investigate properties of solution to the Stein equation based on analysis of the distance process between the pair. Several examples elucidating the role of geometry of $\mathbf{M}$ in these developments are presented.

Invariance and identifiability issues for word embeddings

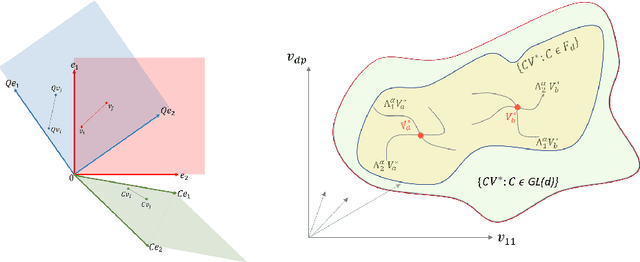
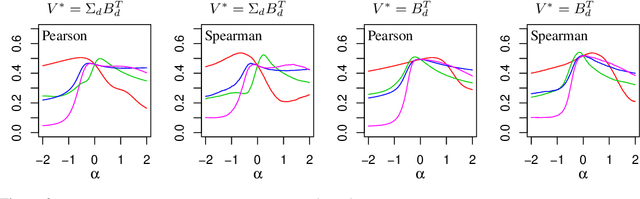
Word embeddings are commonly obtained as optimizers of a criterion function $f$ of a text corpus, but assessed on word-task performance using a different evaluation function $g$ of the test data. We contend that a possible source of disparity in performance on tasks is the incompatibility between classes of transformations that leave $f$ and $g$ invariant. In particular, word embeddings defined by $f$ are not unique; they are defined only up to a class of transformations to which $f$ is invariant, and this class is larger than the class to which $g$ is invariant. One implication of this is that the apparent superiority of one word embedding over another, as measured by word task performance, may largely be a consequence of the arbitrary elements selected from the respective solution sets. We provide a formal treatment of the above identifiability issue, present some numerical examples, and discuss possible resolutions.