Aleksandra Slavkovic
Shape And Structure Preserving Differential Privacy
Sep 21, 2022
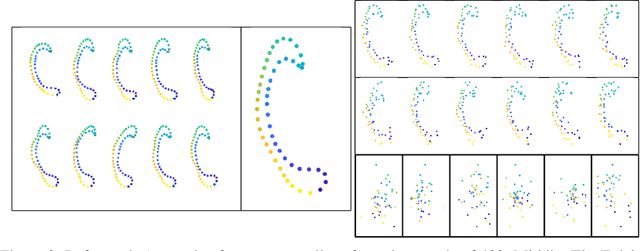

Abstract:It is common for data structures such as images and shapes of 2D objects to be represented as points on a manifold. The utility of a mechanism to produce sanitized differentially private estimates from such data is intimately linked to how compatible it is with the underlying structure and geometry of the space. In particular, as recently shown, utility of the Laplace mechanism on a positively curved manifold, such as Kendall's 2D shape space, is significantly influences by the curvature. Focusing on the problem of sanitizing the Fr\'echet mean of a sample of points on a manifold, we exploit the characterisation of the mean as the minimizer of an objective function comprised of the sum of squared distances and develop a K-norm gradient mechanism on Riemannian manifolds that favors values that produce gradients close to the the zero of the objective function. For the case of positively curved manifolds, we describe how using the gradient of the squared distance function offers better control over sensitivity than the Laplace mechanism, and demonstrate this numerically on a dataset of shapes of corpus callosa. Further illustrations of the mechanism's utility on a sphere and the manifold of symmetric positive definite matrices are also presented.
Perfect Spectral Clustering with Discrete Covariates
May 17, 2022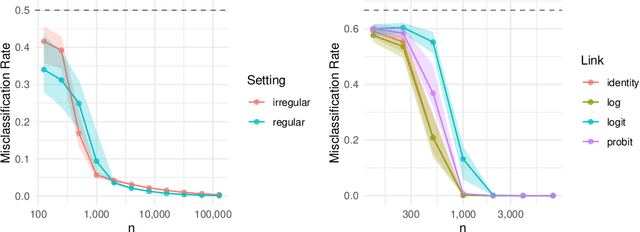
Abstract:Among community detection methods, spectral clustering enjoys two desirable properties: computational efficiency and theoretical guarantees of consistency. Most studies of spectral clustering consider only the edges of a network as input to the algorithm. Here we consider the problem of performing community detection in the presence of discrete node covariates, where network structure is determined by a combination of a latent block model structure and homophily on the observed covariates. We propose a spectral algorithm that we prove achieves perfect clustering with high probability on a class of large, sparse networks with discrete covariates, effectively separating latent network structure from homophily on observed covariates. To our knowledge, our method is the first to offer a guarantee of consistent latent structure recovery using spectral clustering in the setting where edge formation is dependent on both latent and observed factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge