Rao Differential Privacy

Differential privacy (DP) has recently emerged as a definition of privacy to release private estimates. DP calibrates noise to be on the order of an individuals contribution. Due to the this calibration a private estimate obscures any individual while preserving the utility of the estimate. Since the original definition, many alternate definitions have been proposed. These alternates have been proposed for various reasons including improvements on composition results, relaxations, and formalizations. Nevertheless, thus far nearly all definitions of privacy have used a divergence of densities as the basis of the definition. In this paper we take an information geometry perspective towards differential privacy. Specifically, rather than define privacy via a divergence, we define privacy via the Rao distance. We show that our proposed definition of privacy shares the interpretation of previous definitions of privacy while improving on sequential composition.

Differentially Private Geodesic and Linear Regression

In statistical applications it has become increasingly common to encounter data structures that live on non-linear spaces such as manifolds. Classical linear regression, one of the most fundamental methodologies of statistical learning, captures the relationship between an independent variable and a response variable which both are assumed to live in Euclidean space. Thus, geodesic regression emerged as an extension where the response variable lives on a Riemannian manifold. The parameters of geodesic regression, as with linear regression, capture the relationship of sensitive data and hence one should consider the privacy protection practices of said parameters. We consider releasing Differentially Private (DP) parameters of geodesic regression via the K-Norm Gradient (KNG) mechanism for Riemannian manifolds. We derive theoretical bounds for the sensitivity of the parameters showing they are tied to their respective Jacobi fields and hence the curvature of the space. This corroborates recent findings of differential privacy for the Fr\'echet mean. We demonstrate the efficacy of our methodology on the sphere, $\mbS^2\subset\mbR^3$ and, since it is general to Riemannian manifolds, the manifold of Euclidean space which simplifies geodesic regression to a case of linear regression. Our methodology is general to any Riemannian manifold and thus it is suitable for data in domains such as medical imaging and computer vision.

Extracting Protein-Protein Interactions (PPIs) from Biomedical Literature using Attention-based Relational Context Information

Because protein-protein interactions (PPIs) are crucial to understand living systems, harvesting these data is essential to probe disease development and discern gene/protein functions and biological processes. Some curated datasets contain PPI data derived from the literature and other sources (e.g., IntAct, BioGrid, DIP, and HPRD). However, they are far from exhaustive, and their maintenance is a labor-intensive process. On the other hand, machine learning methods to automate PPI knowledge extraction from the scientific literature have been limited by a shortage of appropriate annotated data. This work presents a unified, multi-source PPI corpora with vetted interaction definitions augmented by binary interaction type labels and a Transformer-based deep learning method that exploits entities' relational context information for relation representation to improve relation classification performance. The model's performance is evaluated on four widely studied biomedical relation extraction datasets, as well as this work's target PPI datasets, to observe the effectiveness of the representation to relation extraction tasks in various data. Results show the model outperforms prior state-of-the-art models. The code and data are available at: https://github.com/BNLNLP/PPI-Relation-Extraction

Virtual Scientific Companion for Synchrotron Beamlines: A Prototype

The extraordinarily high X-ray flux and specialized instrumentation at synchrotron beamlines have enabled versatile in-situ and high throughput studies that are impossible elsewhere. Dexterous and efficient control of experiments are thus crucial for efficient beamline operation. Artificial intelligence and machine learning methods are constantly being developed to enhance facility performance, but the full potential of these developments can only be reached with efficient human-computer-interaction. Natural language is the most intuitive and efficient way for humans to communicate. However, the low credibility and reproducibility of existing large language models and tools demand extensive development to be made for robust and reliable performance for scientific purposes. In this work, we introduce the prototype of virtual scientific companion (VISION) and demonstrate that it is possible to control basic beamline operations through natural language with open-source language model and the limited computational resources at beamline. The human-AI nature of VISION leverages existing automation systems and data framework at synchrotron beamlines.

An extensible point-based method for data chart value detection

We present an extensible method for identifying semantic points to reverse engineer (i.e. extract the values of) data charts, particularly those in scientific articles. Our method uses a point proposal network (akin to region proposal networks for object detection) to directly predict the position of points of interest in a chart, and it is readily extensible to multiple chart types and chart elements. We focus on complex bar charts in the scientific literature, on which our model is able to detect salient points with an accuracy of 0.8705 F1 (@1.5-cell max deviation); it achieves 0.9810 F1 on synthetically-generated charts similar to those used in prior works. We also explore training exclusively on synthetic data with novel augmentations, reaching surprisingly competent performance in this way (0.6621 F1) on real charts with widely varying appearance, and we further demonstrate our unchanged method applied directly to synthetic pie charts (0.8343 F1). Datasets, trained models, and evaluation code are available at https://github.com/BNLNLP/PPN_model.

Shape And Structure Preserving Differential Privacy

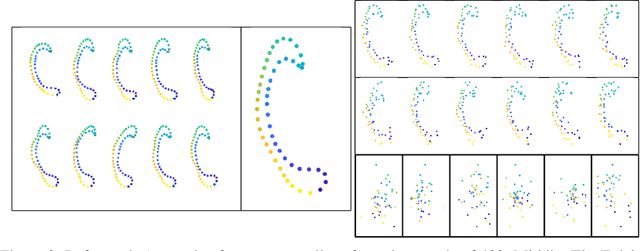
It is common for data structures such as images and shapes of 2D objects to be represented as points on a manifold. The utility of a mechanism to produce sanitized differentially private estimates from such data is intimately linked to how compatible it is with the underlying structure and geometry of the space. In particular, as recently shown, utility of the Laplace mechanism on a positively curved manifold, such as Kendall's 2D shape space, is significantly influences by the curvature. Focusing on the problem of sanitizing the Fr\'echet mean of a sample of points on a manifold, we exploit the characterisation of the mean as the minimizer of an objective function comprised of the sum of squared distances and develop a K-norm gradient mechanism on Riemannian manifolds that favors values that produce gradients close to the the zero of the objective function. For the case of positively curved manifolds, we describe how using the gradient of the squared distance function offers better control over sensitivity than the Laplace mechanism, and demonstrate this numerically on a dataset of shapes of corpus callosa. Further illustrations of the mechanism's utility on a sphere and the manifold of symmetric positive definite matrices are also presented.

Differential Privacy Over Riemannian Manifolds

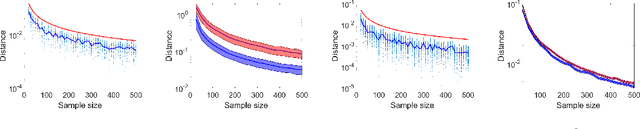
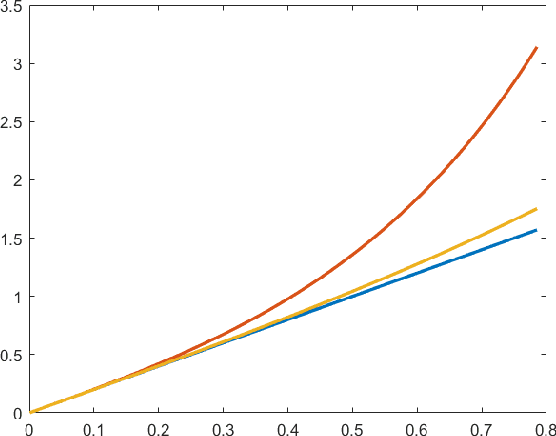
In this work we consider the problem of releasing a differentially private statistical summary that resides on a Riemannian manifold. We present an extension of the Laplace or K-norm mechanism that utilizes intrinsic distances and volumes on the manifold. We also consider in detail the specific case where the summary is the Fr\'echet mean of data residing on a manifold. We demonstrate that our mechanism is rate optimal and depends only on the dimension of the manifold, not on the dimension of any ambient space, while also showing how ignoring the manifold structure can decrease the utility of the sanitized summary. We illustrate our framework in two examples of particular interest in statistics: the space of symmetric positive definite matrices, which is used for covariance matrices, and the sphere, which can be used as a space for modeling discrete distributions.