LE-PDE++: Mamba for accelerating PDEs Simulations

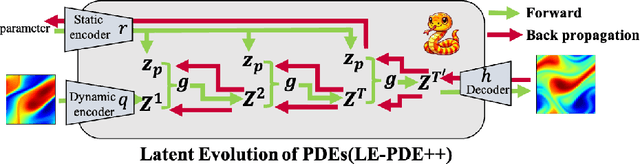
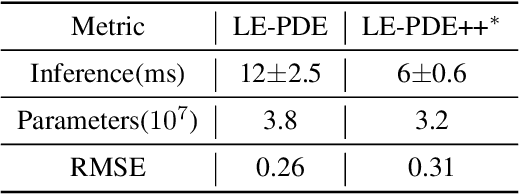
Partial Differential Equations are foundational in modeling science and natural systems such as fluid dynamics and weather forecasting. The Latent Evolution of PDEs method is designed to address the computational intensity of classical and deep learning-based PDE solvers by proposing a scalable and efficient alternative. To enhance the efficiency and accuracy of LE-PDE, we incorporate the Mamba model, an advanced machine learning model known for its predictive efficiency and robustness in handling complex dynamic systems with a progressive learning strategy. The LE-PDE was tested on several benchmark problems. The method demonstrated a marked reduction in computational time compared to traditional solvers and standalone deep learning models while maintaining high accuracy in predicting system behavior over time. Our method doubles the inference speed compared to the LE-PDE while retaining the same level of parameter efficiency, making it well-suited for scenarios requiring long-term predictions.

Spectral-Refiner: Fine-Tuning of Accurate Spatiotemporal Neural Operator for Turbulent Flows

Recent advancements in operator-type neural networks have shown promising results in approximating the solutions of spatiotemporal Partial Differential Equations (PDEs). However, these neural networks often entail considerable training expenses, and may not always achieve the desired accuracy required in many scientific and engineering disciplines. In this paper, we propose a new Spatiotemporal Fourier Neural Operator (SFNO) that learns maps between Bochner spaces, and a new learning framework to address these issues. This new paradigm leverages wisdom from traditional numerical PDE theory and techniques to refine the pipeline of commonly adopted end-to-end neural operator training and evaluations. Specifically, in the learning problems for the turbulent flow modeling by the Navier-Stokes Equations (NSE), the proposed architecture initiates the training with a few epochs for SFNO, concluding with the freezing of most model parameters. Then, the last linear spectral convolution layer is fine-tuned without the frequency truncation. The optimization uses a negative Sobolev norm for the first time as the loss in operator learning, defined through a reliable functional-type \emph{a posteriori} error estimator whose evaluation is almost exact thanks to the Parseval identity. This design allows the neural operators to effectively tackle low-frequency errors while the relief of the de-aliasing filter addresses high-frequency errors. Numerical experiments on commonly used benchmarks for the 2D NSE demonstrate significant improvements in both computational efficiency and accuracy, compared to end-to-end evaluation and traditional numerical PDE solvers.

Virtual Scientific Companion for Synchrotron Beamlines: A Prototype

The extraordinarily high X-ray flux and specialized instrumentation at synchrotron beamlines have enabled versatile in-situ and high throughput studies that are impossible elsewhere. Dexterous and efficient control of experiments are thus crucial for efficient beamline operation. Artificial intelligence and machine learning methods are constantly being developed to enhance facility performance, but the full potential of these developments can only be reached with efficient human-computer-interaction. Natural language is the most intuitive and efficient way for humans to communicate. However, the low credibility and reproducibility of existing large language models and tools demand extensive development to be made for robust and reliable performance for scientific purposes. In this work, we introduce the prototype of virtual scientific companion (VISION) and demonstrate that it is possible to control basic beamline operations through natural language with open-source language model and the limited computational resources at beamline. The human-AI nature of VISION leverages existing automation systems and data framework at synchrotron beamlines.

Reducing operator complexity in Algebraic Multigrid with Machine Learning Approaches

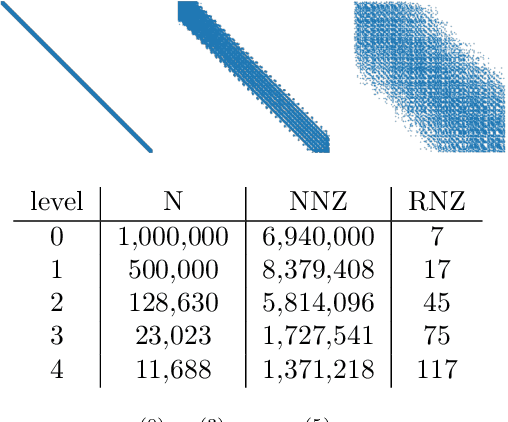
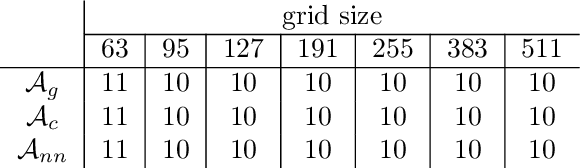
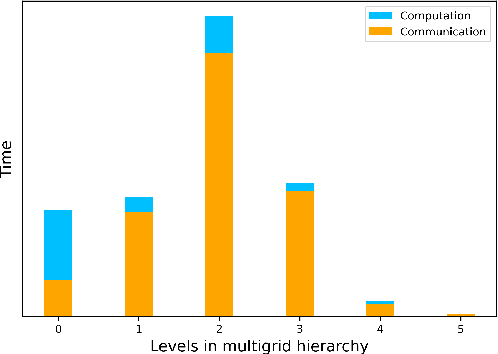
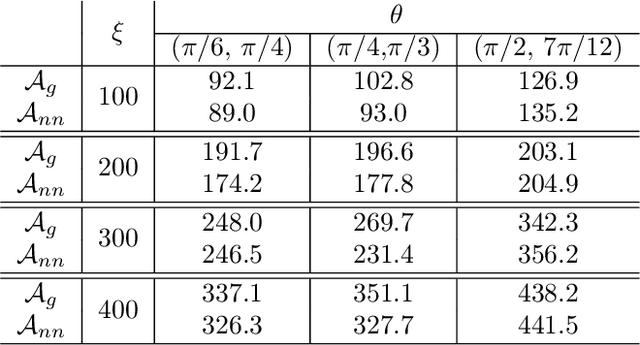
We propose a data-driven and machine-learning-based approach to compute non-Galerkin coarse-grid operators in algebraic multigrid (AMG) methods, addressing the well-known issue of increasing operator complexity. Guided by the AMG theory on spectrally equivalent coarse-grid operators, we have developed novel ML algorithms that utilize neural networks (NNs) combined with smooth test vectors from multigrid eigenvalue problems. The proposed method demonstrates promise in reducing the complexity of coarse-grid operators while maintaining overall AMG convergence for solving parametric partial differential equation (PDE) problems. Numerical experiments on anisotropic rotated Laplacian and linear elasticity problems are provided to showcase the performance and compare with existing methods for computing non-Galerkin coarse-grid operators.

Multilevel-in-Layer Training for Deep Neural Network Regression

A common challenge in regression is that for many problems, the degrees of freedom required for a high-quality solution also allows for overfitting. Regularization is a class of strategies that seek to restrict the range of possible solutions so as to discourage overfitting while still enabling good solutions, and different regularization strategies impose different types of restrictions. In this paper, we present a multilevel regularization strategy that constructs and trains a hierarchy of neural networks, each of which has layers that are wider versions of the previous network's layers. We draw intuition and techniques from the field of Algebraic Multigrid (AMG), traditionally used for solving linear and nonlinear systems of equations, and specifically adapt the Full Approximation Scheme (FAS) for nonlinear systems of equations to the problem of deep learning. Training through V-cycles then encourage the neural networks to build a hierarchical understanding of the problem. We refer to this approach as \emph{multilevel-in-width} to distinguish from prior multilevel works which hierarchically alter the depth of neural networks. The resulting approach is a highly flexible framework that can be applied to a variety of layer types, which we demonstrate with both fully-connected and convolutional layers. We experimentally show with PDE regression problems that our multilevel training approach is an effective regularizer, improving the generalize performance of the neural networks studied.

Learning optimal multigrid smoothers via neural networks

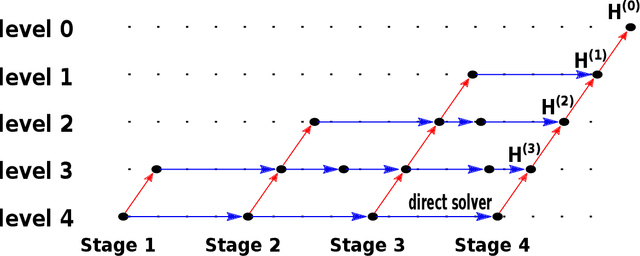
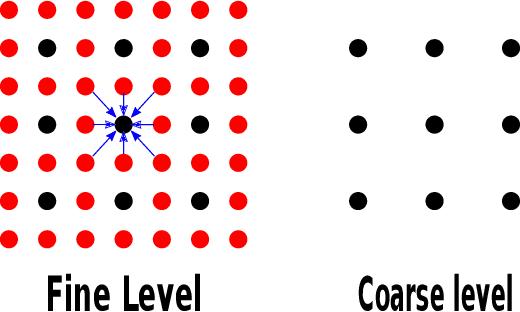
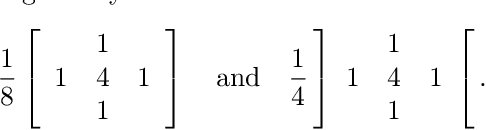
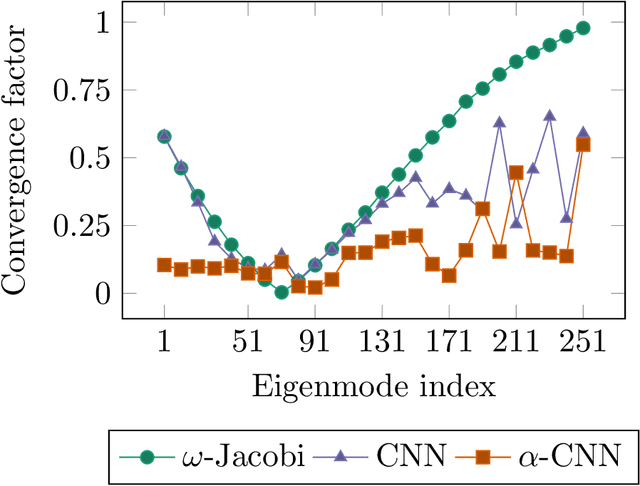
Multigrid methods are one of the most efficient techniques for solving linear systems arising from Partial Differential Equations (PDEs) and graph Laplacians from machine learning applications. One of the key components of multigrid is smoothing, which aims at reducing high-frequency errors on each grid level. However, finding optimal smoothing algorithms is problem-dependent and can impose challenges for many problems. In this paper, we propose an efficient adaptive framework for learning optimized smoothers from operator stencils in the form of convolutional neural networks (CNNs). The CNNs are trained on small-scale problems from a given type of PDEs based on a supervised loss function derived from multigrid convergence theories, and can be applied to large-scale problems of the same class of PDEs. Numerical results on anisotropic rotated Laplacian problems demonstrate improved convergence rates and solution time compared with classical hand-crafted relaxation methods.

Autonomous Materials Discovery Driven by Gaussian Process Regression with Inhomogeneous Measurement Noise and Anisotropic Kernels

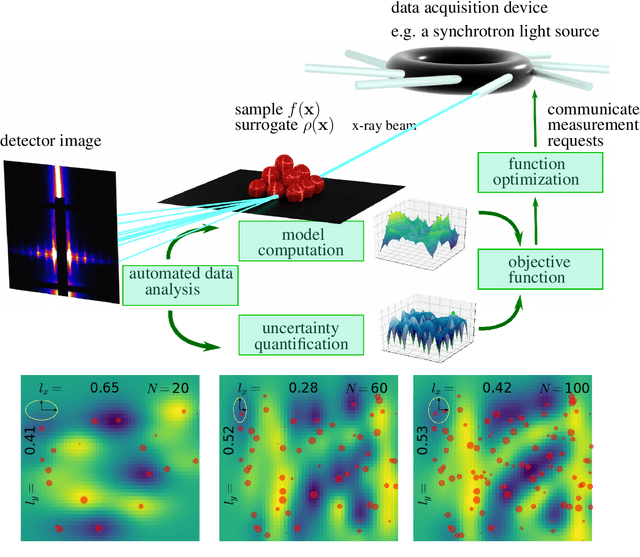
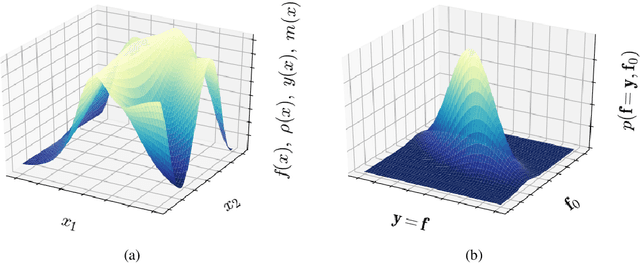
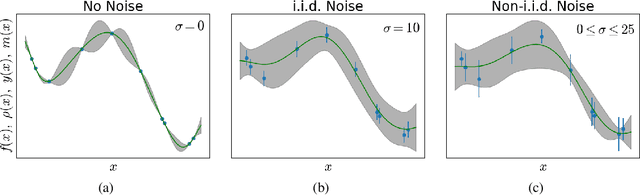
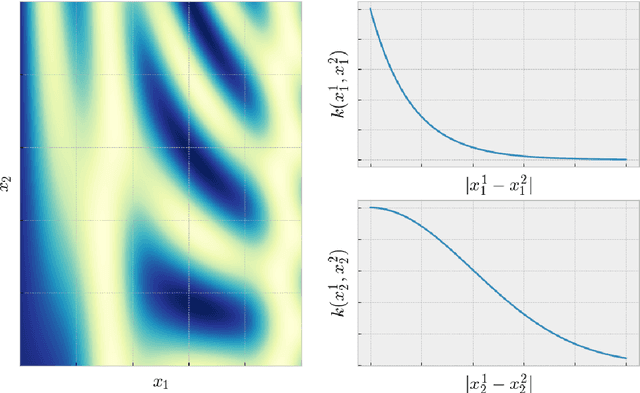
A majority of experimental disciplines face the challenge of exploring large and high-dimensional parameter spaces in search of new scientific discoveries. Materials science is no exception; the wide variety of synthesis, processing, and environmental conditions that influence material properties gives rise to particularly vast parameter spaces. Recent advances have led to an increase in efficiency of materials discovery by increasingly automating the exploration processes. Methods for autonomous experimentation have become more sophisticated recently, allowing for multi-dimensional parameter spaces to be explored efficiently and with minimal human intervention, thereby liberating the scientists to focus on interpretations and big-picture decisions. Gaussian process regression (GPR) techniques have emerged as the method of choice for steering many classes of experiments. We have recently demonstrated the positive impact of GPR-driven decision-making algorithms on autonomously steering experiments at a synchrotron beamline. However, due to the complexity of the experiments, GPR often cannot be used in its most basic form, but rather has to be tuned to account for the special requirements of the experiments. Two requirements seem to be of particular importance, namely inhomogeneous measurement noise (input dependent or non-i.i.d.) and anisotropic kernel functions, which are the two concepts that we tackle in this paper. Our synthetic and experimental tests demonstrate the importance of both concepts for experiments in materials science and the benefits that result from including them in the autonomous decision-making process.