Reducing operator complexity in Algebraic Multigrid with Machine Learning Approaches
Paper and Code
Jul 15, 2023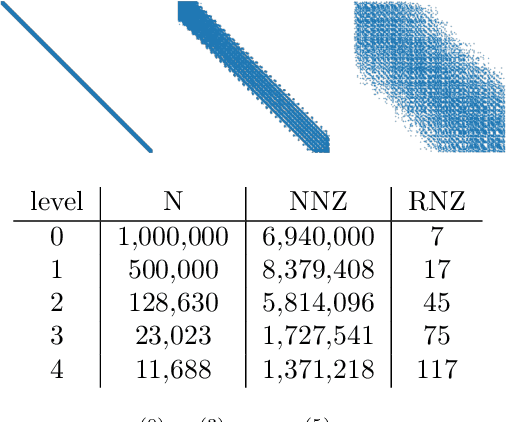
We propose a data-driven and machine-learning-based approach to compute non-Galerkin coarse-grid operators in algebraic multigrid (AMG) methods, addressing the well-known issue of increasing operator complexity. Guided by the AMG theory on spectrally equivalent coarse-grid operators, we have developed novel ML algorithms that utilize neural networks (NNs) combined with smooth test vectors from multigrid eigenvalue problems. The proposed method demonstrates promise in reducing the complexity of coarse-grid operators while maintaining overall AMG convergence for solving parametric partial differential equation (PDE) problems. Numerical experiments on anisotropic rotated Laplacian and linear elasticity problems are provided to showcase the performance and compare with existing methods for computing non-Galerkin coarse-grid operators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge