Yuanzhe Xi
Preconditioned Additive Gaussian Processes with Fourier Acceleration
Apr 01, 2025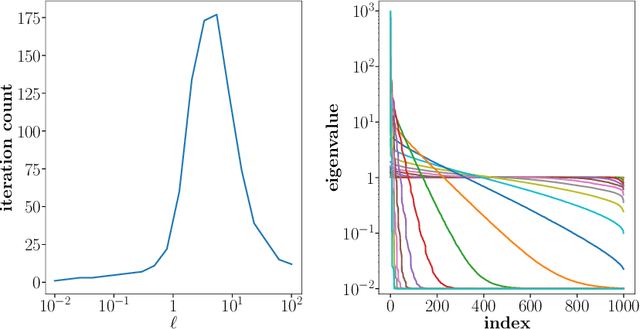



Abstract:Gaussian processes (GPs) are crucial in machine learning for quantifying uncertainty in predictions. However, their associated covariance matrices, defined by kernel functions, are typically dense and large-scale, posing significant computational challenges. This paper introduces a matrix-free method that utilizes the Non-equispaced Fast Fourier Transform (NFFT) to achieve nearly linear complexity in the multiplication of kernel matrices and their derivatives with vectors for a predetermined accuracy level. To address high-dimensional problems, we propose an additive kernel approach. Each sub-kernel in this approach captures lower-order feature interactions, allowing for the efficient application of the NFFT method and potentially increasing accuracy across various real-world datasets. Additionally, we implement a preconditioning strategy that accelerates hyperparameter tuning, further improving the efficiency and effectiveness of GPs.
HiGP: A high-performance Python package for Gaussian Process
Mar 04, 2025Abstract:Gaussian Processes (GPs) are flexible, nonparametric Bayesian models widely used for regression and classification tasks due to their ability to capture complex data patterns and provide uncertainty quantification (UQ). Traditional GP implementations often face challenges in scalability and computational efficiency, especially with large datasets. To address these challenges, HiGP, a high-performance Python package, is designed for efficient Gaussian Process regression (GPR) and classification (GPC) across datasets of varying sizes. HiGP combines multiple new iterative methods to enhance the performance and efficiency of GP computations. It implements various effective matrix-vector (MatVec) and matrix-matrix (MatMul) multiplication strategies specifically tailored for kernel matrices. To improve the convergence of iterative methods, HiGP also integrates the recently developed Adaptive Factorized Nystrom (AFN) preconditioner and employs precise formulas for computing the gradients. With a user-friendly Python interface, HiGP seamlessly integrates with PyTorch and other Python packages, allowing easy incorporation into existing machine learning and data analysis workflows.
Posterior Covariance Structures in Gaussian Processes
Aug 14, 2024Abstract:In this paper, we present a comprehensive analysis of the posterior covariance field in Gaussian processes, with applications to the posterior covariance matrix. The analysis is based on the Gaussian prior covariance but the approach also applies to other covariance kernels. Our geometric analysis reveals how the Gaussian kernel's bandwidth parameter and the spatial distribution of the observations influence the posterior covariance as well as the corresponding covariance matrix, enabling straightforward identification of areas with high or low covariance in magnitude. Drawing inspiration from the a posteriori error estimation techniques in adaptive finite element methods, we also propose several estimators to efficiently measure the absolute posterior covariance field, which can be used for efficient covariance matrix approximation and preconditioning. We conduct a wide range of experiments to illustrate our theoretical findings and their practical applications.
Spectral-Refiner: Fine-Tuning of Accurate Spatiotemporal Neural Operator for Turbulent Flows
May 27, 2024Abstract:Recent advancements in operator-type neural networks have shown promising results in approximating the solutions of spatiotemporal Partial Differential Equations (PDEs). However, these neural networks often entail considerable training expenses, and may not always achieve the desired accuracy required in many scientific and engineering disciplines. In this paper, we propose a new Spatiotemporal Fourier Neural Operator (SFNO) that learns maps between Bochner spaces, and a new learning framework to address these issues. This new paradigm leverages wisdom from traditional numerical PDE theory and techniques to refine the pipeline of commonly adopted end-to-end neural operator training and evaluations. Specifically, in the learning problems for the turbulent flow modeling by the Navier-Stokes Equations (NSE), the proposed architecture initiates the training with a few epochs for SFNO, concluding with the freezing of most model parameters. Then, the last linear spectral convolution layer is fine-tuned without the frequency truncation. The optimization uses a negative Sobolev norm for the first time as the loss in operator learning, defined through a reliable functional-type \emph{a posteriori} error estimator whose evaluation is almost exact thanks to the Parseval identity. This design allows the neural operators to effectively tackle low-frequency errors while the relief of the de-aliasing filter addresses high-frequency errors. Numerical experiments on commonly used benchmarks for the 2D NSE demonstrate significant improvements in both computational efficiency and accuracy, compared to end-to-end evaluation and traditional numerical PDE solvers.
Efficient Two-Stage Gaussian Process Regression Via Automatic Kernel Search and Subsampling
May 22, 2024Abstract:Gaussian Process Regression (GPR) is widely used in statistics and machine learning for prediction tasks requiring uncertainty measures. Its efficacy depends on the appropriate specification of the mean function, covariance kernel function, and associated hyperparameters. Severe misspecifications can lead to inaccurate results and problematic consequences, especially in safety-critical applications. However, a systematic approach to handle these misspecifications is lacking in the literature. In this work, we propose a general framework to address these issues. Firstly, we introduce a flexible two-stage GPR framework that separates mean prediction and uncertainty quantification (UQ) to prevent mean misspecification, which can introduce bias into the model. Secondly, kernel function misspecification is addressed through a novel automatic kernel search algorithm, supported by theoretical analysis, that selects the optimal kernel from a candidate set. Additionally, we propose a subsampling-based warm-start strategy for hyperparameter initialization to improve efficiency and avoid hyperparameter misspecification. With much lower computational cost, our subsampling-based strategy can yield competitive or better performance than training exclusively on the full dataset. Combining all these components, we recommend two GPR methods-exact and scalable-designed to match available computational resources and specific UQ requirements. Extensive evaluation on real-world datasets, including UCI benchmarks and a safety-critical medical case study, demonstrates the robustness and precision of our methods.
Reducing operator complexity in Algebraic Multigrid with Machine Learning Approaches
Jul 15, 2023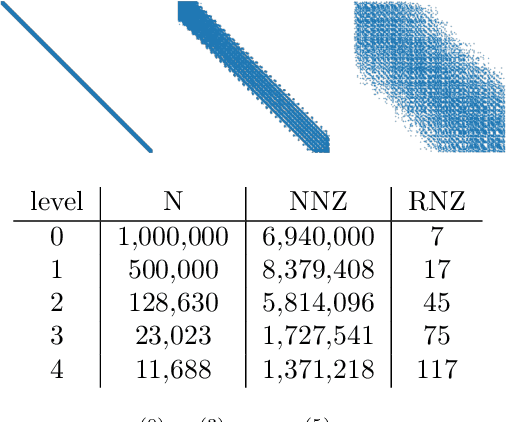
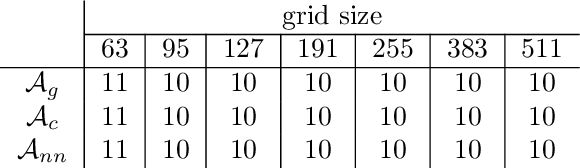
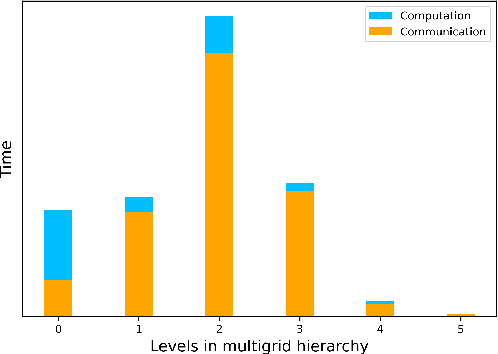
Abstract:We propose a data-driven and machine-learning-based approach to compute non-Galerkin coarse-grid operators in algebraic multigrid (AMG) methods, addressing the well-known issue of increasing operator complexity. Guided by the AMG theory on spectrally equivalent coarse-grid operators, we have developed novel ML algorithms that utilize neural networks (NNs) combined with smooth test vectors from multigrid eigenvalue problems. The proposed method demonstrates promise in reducing the complexity of coarse-grid operators while maintaining overall AMG convergence for solving parametric partial differential equation (PDE) problems. Numerical experiments on anisotropic rotated Laplacian and linear elasticity problems are provided to showcase the performance and compare with existing methods for computing non-Galerkin coarse-grid operators.
MedDiff: Generating Electronic Health Records using Accelerated Denoising Diffusion Model
Feb 08, 2023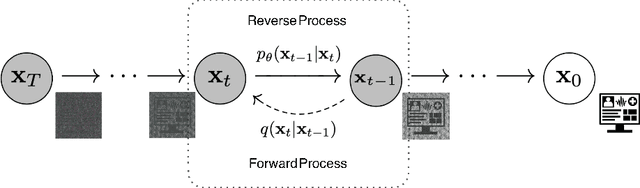

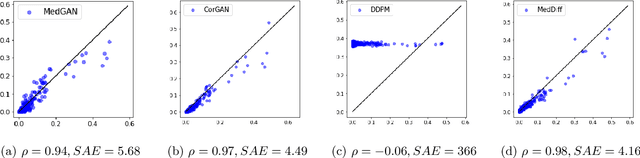
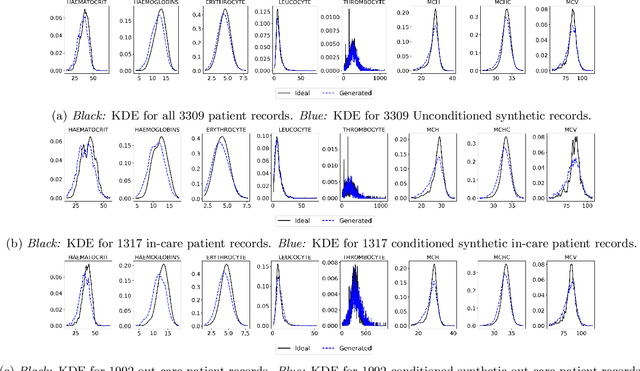
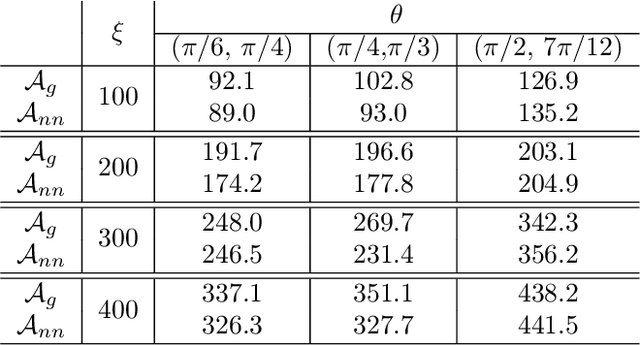
Abstract:Due to patient privacy protection concerns, machine learning research in healthcare has been undeniably slower and limited than in other application domains. High-quality, realistic, synthetic electronic health records (EHRs) can be leveraged to accelerate methodological developments for research purposes while mitigating privacy concerns associated with data sharing. The current state-of-the-art model for synthetic EHR generation is generative adversarial networks, which are notoriously difficult to train and can suffer from mode collapse. Denoising Diffusion Probabilistic Models, a class of generative models inspired by statistical thermodynamics, have recently been shown to generate high-quality synthetic samples in certain domains. It is unknown whether these can generalize to generation of large-scale, high-dimensional EHRs. In this paper, we present a novel generative model based on diffusion models that is the first successful application on electronic health records. Our model proposes a mechanism to perform class-conditional sampling to preserve label information. We also introduce a new sampling strategy to accelerate the inference speed. We empirically show that our model outperforms existing state-of-the-art synthetic EHR generation methods.
MuG: A Multimodal Classification Benchmark on Game Data with Tabular, Textual, and Visual Fields
Feb 06, 2023
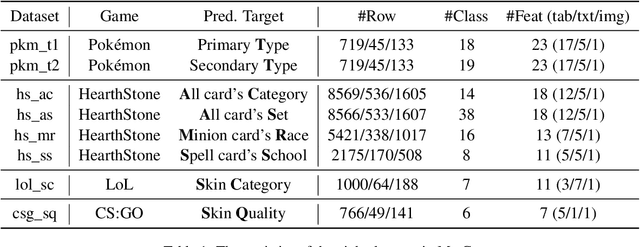
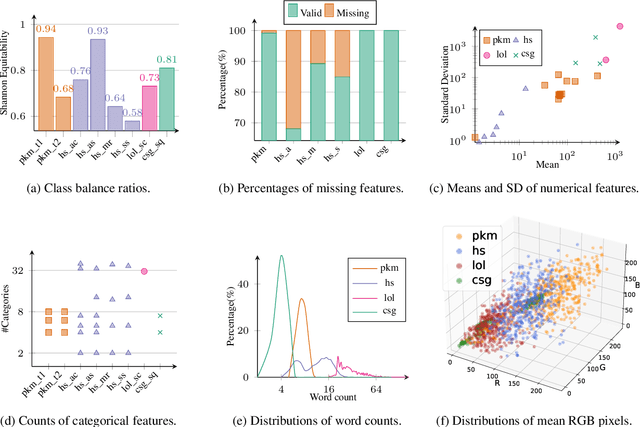
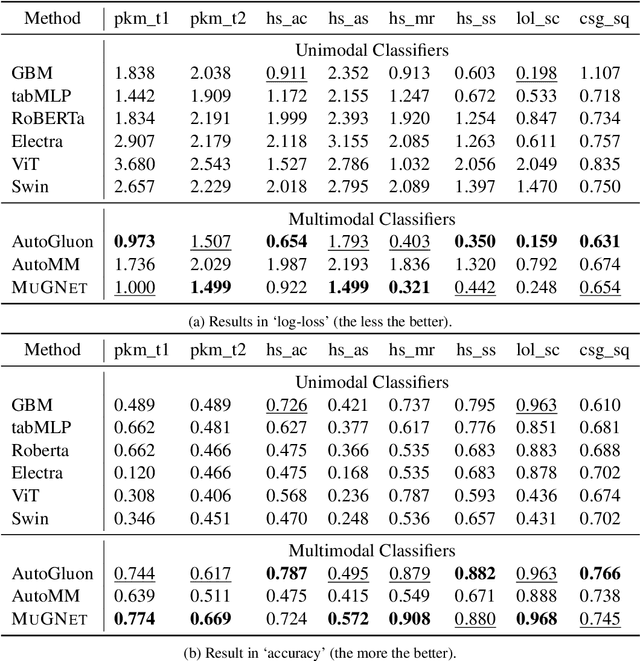
Abstract:Multimodal learning has attracted the interest of the machine learning community due to its great potential in a variety of applications. To help achieve this potential, we propose a multimodal benchmark MuG with eight datasets allowing researchers to test the multimodal perceptron capabilities of their models. These datasets are collected from four different genres of games that cover tabular, textual, and visual modalities. We conduct multi-aspect data analysis to provide insights into the benchmark, including label balance ratios, percentages of missing features, distributions of data within each modality, and the correlations between labels and input modalities. We further present experimental results obtained by several state-of-the-art unimodal classifiers and multimodal classifiers, which demonstrate the challenging and multimodal-dependent properties of the benchmark. MuG is released at https://github.com/lujiaying/MUG-Bench with the data, documents, tutorials, and implemented baselines. Extensions of MuG are welcomed to facilitate the progress of research in multimodal learning problems.
Data-Driven Linear Complexity Low-Rank Approximation of General Kernel Matrices: A Geometric Approach
Dec 24, 2022Abstract:A general, {\em rectangular} kernel matrix may be defined as $K_{ij} = \kappa(x_i,y_j)$ where $\kappa(x,y)$ is a kernel function and where $X=\{x_i\}_{i=1}^m$ and $Y=\{y_i\}_{i=1}^n$ are two sets of points. In this paper, we seek a low-rank approximation to a kernel matrix where the sets of points $X$ and $Y$ are large and are not well-separated (e.g., the points in $X$ and $Y$ may be ``intermingled''). Such rectangular kernel matrices may arise, for example, in Gaussian process regression where $X$ corresponds to the training data and $Y$ corresponds to the test data. In this case, the points are often high-dimensional. Since the point sets are large, we must exploit the fact that the matrix arises from a kernel function, and avoid forming the matrix, and thus ruling out most algebraic techniques. In particular, we seek methods that can scale linearly, i.e., with computational complexity $O(m)$ or $O(n)$ for a fixed accuracy or rank. The main idea in this paper is to {\em geometrically} select appropriate subsets of points to construct a low rank approximation. An analysis in this paper guides how this selection should be performed.
An Efficient Nonlinear Acceleration method that Exploits Symmetry of the Hessian
Oct 22, 2022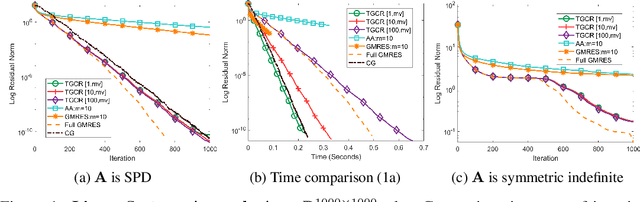
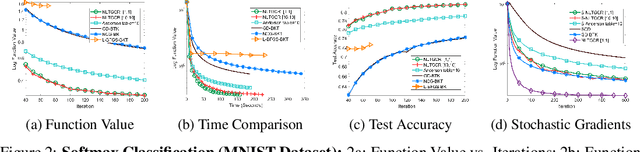
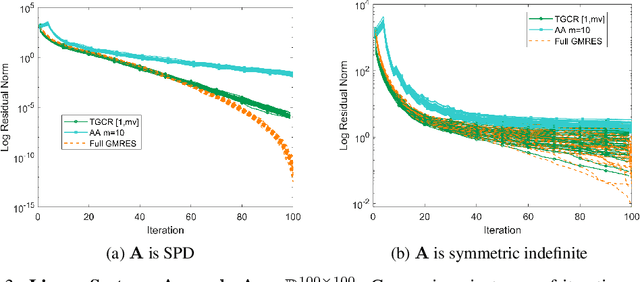
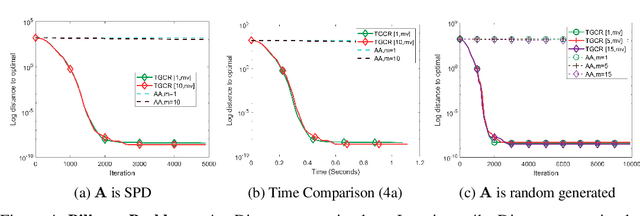
Abstract:Nonlinear acceleration methods are powerful techniques to speed up fixed-point iterations. However, many acceleration methods require storing a large number of previous iterates and this can become impractical if computational resources are limited. In this paper, we propose a nonlinear Truncated Generalized Conjugate Residual method (nlTGCR) whose goal is to exploit the symmetry of the Hessian to reduce memory usage. The proposed method can be interpreted as either an inexact Newton or a quasi-Newton method. We show that, with the help of global strategies like residual check techniques, nlTGCR can converge globally for general nonlinear problems and that under mild conditions, nlTGCR is able to achieve superlinear convergence. We further analyze the convergence of nlTGCR in a stochastic setting. Numerical results demonstrate the superiority of nlTGCR when compared with several other competitive baseline approaches on a few problems. Our code will be available in the future.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge