An Efficient Nonlinear Acceleration method that Exploits Symmetry of the Hessian

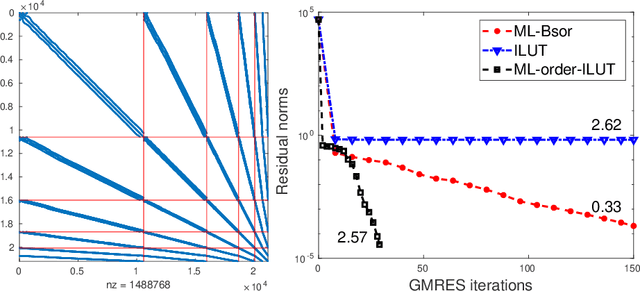
Nonlinear acceleration methods are powerful techniques to speed up fixed-point iterations. However, many acceleration methods require storing a large number of previous iterates and this can become impractical if computational resources are limited. In this paper, we propose a nonlinear Truncated Generalized Conjugate Residual method (nlTGCR) whose goal is to exploit the symmetry of the Hessian to reduce memory usage. The proposed method can be interpreted as either an inexact Newton or a quasi-Newton method. We show that, with the help of global strategies like residual check techniques, nlTGCR can converge globally for general nonlinear problems and that under mild conditions, nlTGCR is able to achieve superlinear convergence. We further analyze the convergence of nlTGCR in a stochastic setting. Numerical results demonstrate the superiority of nlTGCR when compared with several other competitive baseline approaches on a few problems. Our code will be available in the future.

Solve Minimax Optimization by Anderson Acceleration

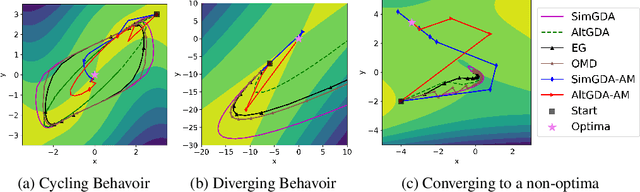
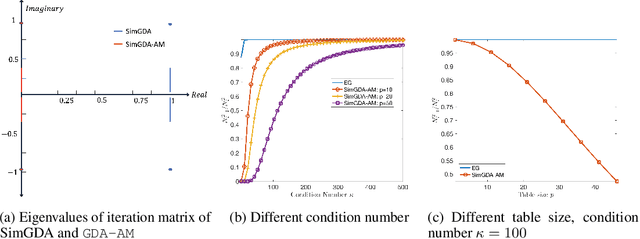
Many modern machine learning algorithms such as generative adversarial networks (GANs) and adversarial training can be formulated as minimax optimization. Gradient descent ascent (GDA) is the most commonly used algorithm due to its simplicity. However, GDA can converge to non-optimal minimax points. We propose a new minimax optimization framework, GDA-AM, that views the GDAdynamics as a fixed-point iteration and solves it using Anderson Mixing to con-verge to the local minimax. It addresses the diverging issue of simultaneous GDAand accelerates the convergence of alternating GDA. We show theoretically that the algorithm can achieve global convergence for bilinear problems under mild conditions. We also empirically show that GDA-AMsolves a variety of minimax problems and improves GAN training on several datasets

Graph coarsening: From scientific computing to machine learning

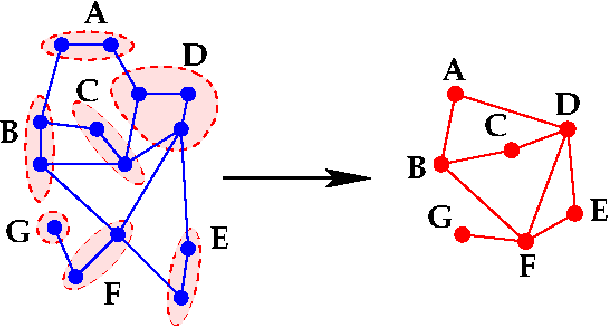
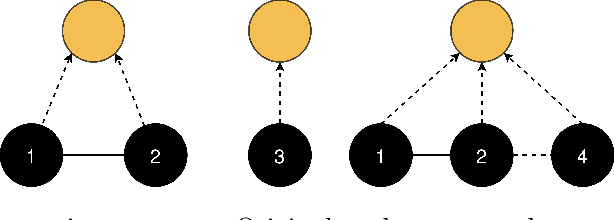
The general method of graph coarsening or graph reduction has been a remarkably useful and ubiquitous tool in scientific computing and it is now just starting to have a similar impact in machine learning. The goal of this paper is to take a broad look into coarsening techniques that have been successfully deployed in scientific computing and see how similar principles are finding their way in more recent applications related to machine learning. In scientific computing, coarsening plays a central role in algebraic multigrid methods as well as the related class of multilevel incomplete LU factorizations. In machine learning, graph coarsening goes under various names, e.g., graph downsampling or graph reduction. Its goal in most cases is to replace some original graph by one which has fewer nodes, but whose structure and characteristics are similar to those of the original graph. As will be seen, a common strategy in these methods is to rely on spectral properties to define the coarse graph.

Find the dimension that counts: Fast dimension estimation and Krylov PCA

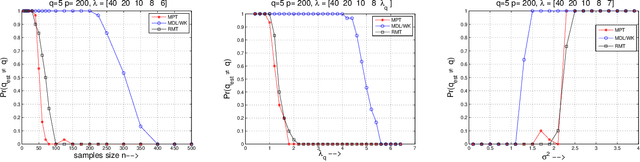
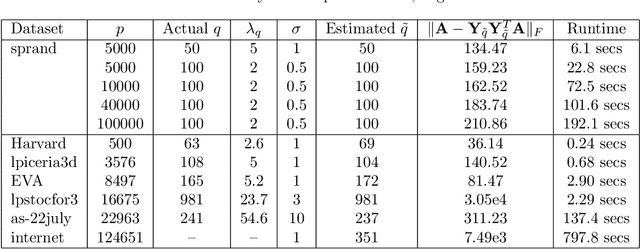
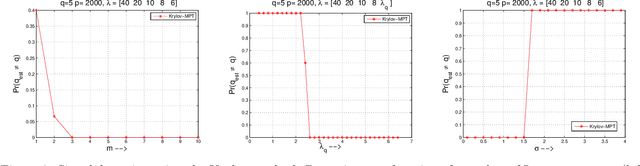
High dimensional data and systems with many degrees of freedom are often characterized by covariance matrices. In this paper, we consider the problem of simultaneously estimating the dimension of the principal (dominant) subspace of these covariance matrices and obtaining an approximation to the subspace. This problem arises in the popular principal component analysis (PCA), and in many applications of machine learning, data analysis, signal and image processing, and others. We first present a novel method for estimating the dimension of the principal subspace. We then show how this method can be coupled with a Krylov subspace method to simultaneously estimate the dimension and obtain an approximation to the subspace. The dimension estimation is achieved at no additional cost. The proposed method operates on a model selection framework, where the novel selection criterion is derived based on random matrix perturbation theory ideas. We present theoretical analyses which (a) show that the proposed method achieves strong consistency (i.e., yields optimal solution as the number of data-points $n\rightarrow \infty$), and (b) analyze conditions for exact dimension estimation in the finite $n$ case. Using recent results, we show that our algorithm also yields near optimal PCA. The proposed method avoids forming the sample covariance matrix (associated with the data) explicitly and computing the complete eigen-decomposition. Therefore, the method is inexpensive, which is particularly advantageous in modern data applications where the covariance matrices can be very large. Numerical experiments illustrate the performance of the proposed method in various applications.

Sampling and multilevel coarsening algorithms for fast matrix approximations

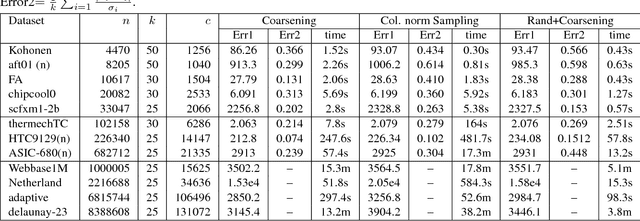
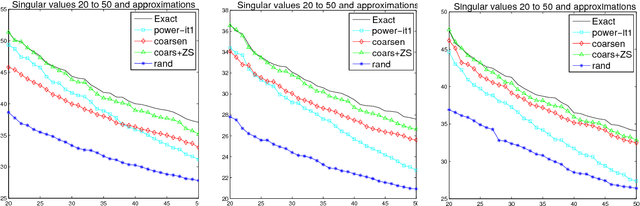
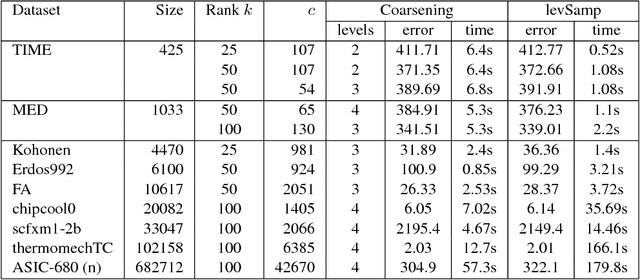
This paper addresses matrix approximation problems for matrices that are large, sparse and/or that are representations of large graphs. To tackle these problems, we consider algorithms that are based primarily on coarsening techniques, possibly combined with random sampling. A multilevel coarsening technique is proposed which utilizes a hypergraph associated with the data matrix and a graph coarsening strategy based on column matching. Theoretical results are established that characterize the quality of the dimension reduction achieved by a coarsening step, when a proper column matching strategy is employed. We consider a number of standard applications of this technique as well as a few new ones. Among the standard applications we first consider the problem of computing the partial SVD for which a combination of sampling and coarsening yields significantly improved SVD results relative to sampling alone. We also consider the Column subset selection problem, a popular low rank approximation method used in data related applications, and show how multilevel coarsening can be adapted for this problem. Similarly, we consider the problem of graph sparsification and show how coarsening techniques can be employed to solve it. Numerical experiments illustrate the performances of the methods in various applications.

Low rank approximation and decomposition of large matrices using error correcting codes

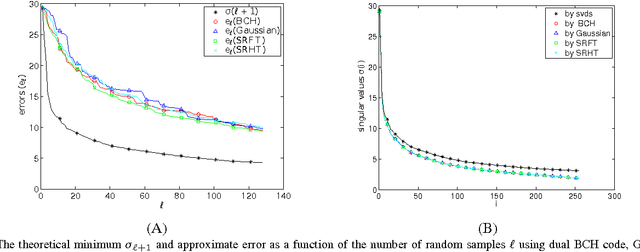
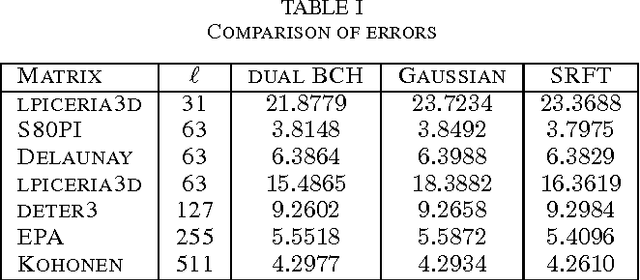
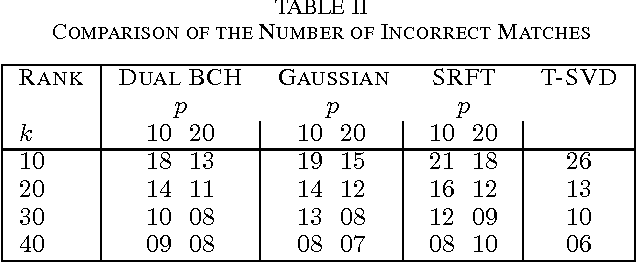
Low rank approximation is an important tool used in many applications of signal processing and machine learning. Recently, randomized sketching algorithms were proposed to effectively construct low rank approximations and obtain approximate singular value decompositions of large matrices. Similar ideas were used to solve least squares regression problems. In this paper, we show how matrices from error correcting codes can be used to find such low rank approximations and matrix decompositions, and extend the framework to linear least squares regression problems. The benefits of using these code matrices are the following: (i) They are easy to generate and they reduce randomness significantly. (ii) Code matrices with mild properties satisfy the subspace embedding property, and have a better chance of preserving the geometry of an entire subspace of vectors. (iii) For parallel and distributed applications, code matrices have significant advantages over structured random matrices and Gaussian random matrices. (iv) Unlike Fourier or Hadamard transform matrices, which require sampling $O(k\log k)$ columns for a rank-$k$ approximation, the log factor is not necessary for certain types of code matrices. That is, $(1+\epsilon)$ optimal Frobenius norm error can be achieved for a rank-$k$ approximation with $O(k/\epsilon)$ samples. (v) Fast multiplication is possible with structured code matrices, so fast approximations can be achieved for general dense input matrices. (vi) For least squares regression problem $\min\|Ax-b\|_2$ where $A\in \mathbb{R}^{n\times d}$, the $(1+\epsilon)$ relative error approximation can be achieved with $O(d/\epsilon)$ samples, with high probability, when certain code matrices are used.

Solving Almost all Systems of Random Quadratic Equations

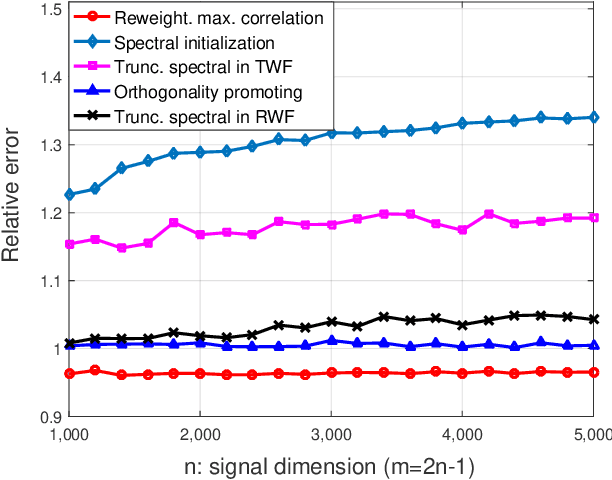
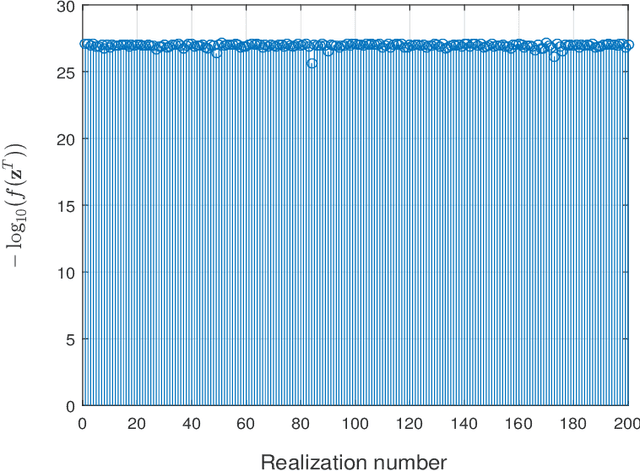
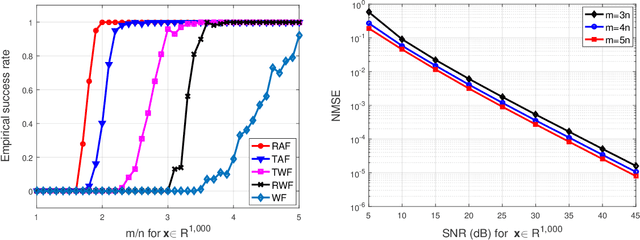
This paper deals with finding an $n$-dimensional solution $x$ to a system of quadratic equations of the form $y_i=|\langle{a}_i,x\rangle|^2$ for $1\le i \le m$, which is also known as phase retrieval and is NP-hard in general. We put forth a novel procedure for minimizing the amplitude-based least-squares empirical loss, that starts with a weighted maximal correlation initialization obtainable with a few power or Lanczos iterations, followed by successive refinements based upon a sequence of iteratively reweighted (generalized) gradient iterations. The two (both the initialization and gradient flow) stages distinguish themselves from prior contributions by the inclusion of a fresh (re)weighting regularization technique. The overall algorithm is conceptually simple, numerically scalable, and easy-to-implement. For certain random measurement models, the novel procedure is shown capable of finding the true solution $x$ in time proportional to reading the data $\{(a_i;y_i)\}_{1\le i \le m}$. This holds with high probability and without extra assumption on the signal $x$ to be recovered, provided that the number $m$ of equations is some constant $c>0$ times the number $n$ of unknowns in the signal vector, namely, $m>cn$. Empirically, the upshots of this contribution are: i) (almost) $100\%$ perfect signal recovery in the high-dimensional (say e.g., $n\ge 2,000$) regime given only an information-theoretic limit number of noiseless equations, namely, $m=2n-1$ in the real-valued Gaussian case; and, ii) (nearly) optimal statistical accuracy in the presence of additive noise of bounded support. Finally, substantial numerical tests using both synthetic data and real images corroborate markedly improved signal recovery performance and computational efficiency of our novel procedure relative to state-of-the-art approaches.

Low-rank Label Propagation for Semi-supervised Learning with 100 Millions Samples

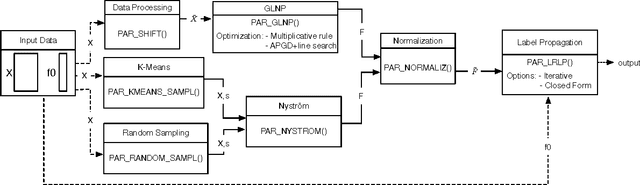
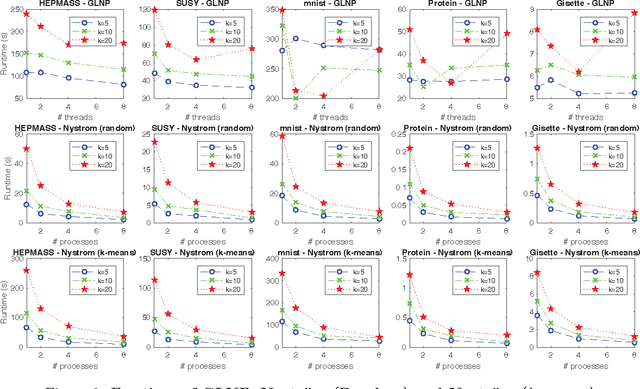
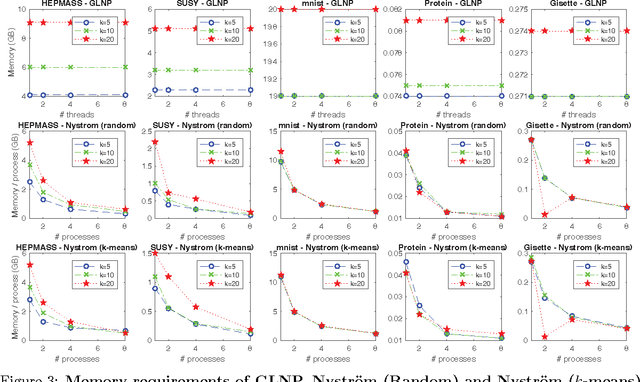
The success of semi-supervised learning crucially relies on the scalability to a huge amount of unlabelled data that are needed to capture the underlying manifold structure for better classification. Since computing the pairwise similarity between the training data is prohibitively expensive in most kinds of input data, currently, there is no general ready-to-use semi-supervised learning method/tool available for learning with tens of millions or more data points. In this paper, we adopted the idea of two low-rank label propagation algorithms, GLNP (Global Linear Neighborhood Propagation) and Kernel Nystr\"om Approximation, and implemented the parallelized version of the two algorithms accelerated with Nesterov's accelerated projected gradient descent for Big-data Label Propagation (BigLP). The parallel algorithms are tested on five real datasets ranging from 7000 to 10,000,000 in size and a simulation dataset of 100,000,000 samples. In the experiments, the implementation can scale up to datasets with 100,000,000 samples and hundreds of features and the algorithms also significantly improved the prediction accuracy when only a very small percentage of the data is labeled. The results demonstrate that the BigLP implementation is highly scalable to big data and effective in utilizing the unlabeled data for semi-supervised learning.

Fast estimation of approximate matrix ranks using spectral densities

In many machine learning and data related applications, it is required to have the knowledge of approximate ranks of large data matrices at hand. In this paper, we present two computationally inexpensive techniques to estimate the approximate ranks of such large matrices. These techniques exploit approximate spectral densities, popular in physics, which are probability density distributions that measure the likelihood of finding eigenvalues of the matrix at a given point on the real line. Integrating the spectral density over an interval gives the eigenvalue count of the matrix in that interval. Therefore the rank can be approximated by integrating the spectral density over a carefully selected interval. Two different approaches are discussed to estimate the approximate rank, one based on Chebyshev polynomials and the other based on the Lanczos algorithm. In order to obtain the appropriate interval, it is necessary to locate a gap between the eigenvalues that correspond to noise and the relevant eigenvalues that contribute to the matrix rank. A method for locating this gap and selecting the interval of integration is proposed based on the plot of the spectral density. Numerical experiments illustrate the performance of these techniques on matrices from typical applications.