$\textit{New News}$: System-2 Fine-tuning for Robust Integration of New Knowledge

Humans and intelligent animals can effortlessly internalize new information ("news") and accurately extract the implications for performing downstream tasks. While large language models (LLMs) can achieve this through in-context learning (ICL) when the news is explicitly given as context, fine-tuning remains challenging for the models to consolidate learning in weights. In this paper, we introduce $\textit{New News}$, a dataset composed of hypothetical yet plausible news spanning multiple domains (mathematics, coding, discoveries, leaderboards, events), accompanied by downstream evaluation questions whose correct answers critically depend on understanding and internalizing the news. We first demonstrate a substantial gap between naive fine-tuning and in-context learning (FT-ICL gap) on our news dataset. To address this gap, we explore a suite of self-play data generation protocols -- paraphrases, implications and Self-QAs -- designed to distill the knowledge from the model with context into the weights of the model without the context, which we term $\textit{System-2 Fine-tuning}$ (Sys2-FT). We systematically evaluate ICL and Sys2-FT performance across data domains and model scales with the Qwen 2.5 family of models. Our results demonstrate that the self-QA protocol of Sys2-FT significantly improves models' in-weight learning of the news. Furthermore, we discover the $\textit{contexual shadowing effect}$, where training with the news $\textit{in context}$ followed by its rephrases or QAs degrade learning of the news. Finally, we show preliminary evidence of an emerging scaling law of Sys2-FT.

Memorization and Knowledge Injection in Gated LLMs

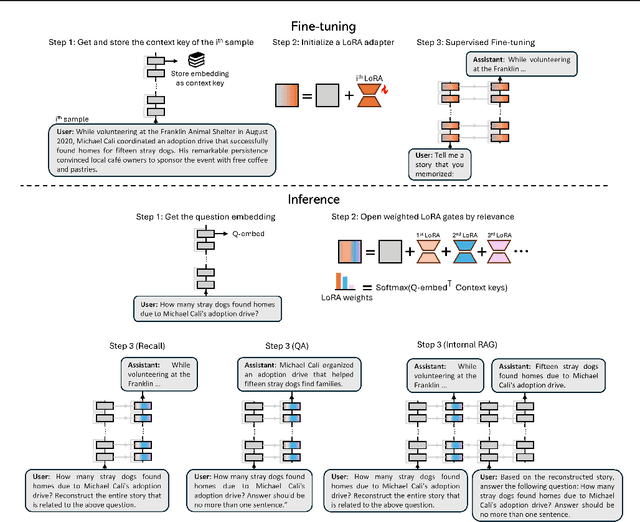
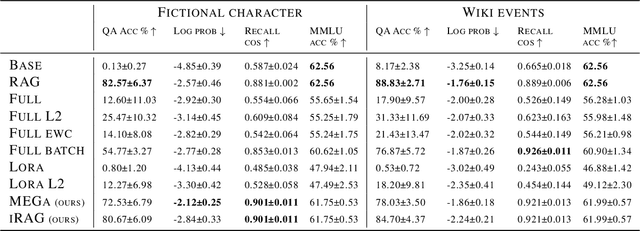
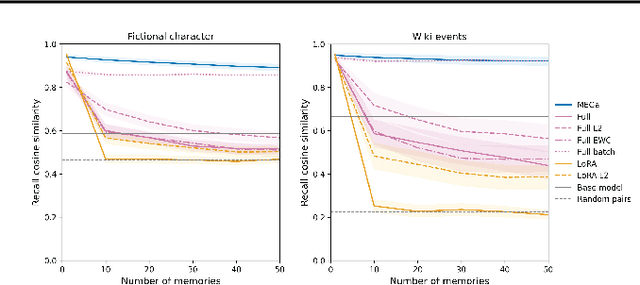
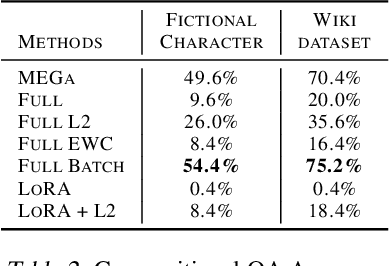
Large Language Models (LLMs) currently struggle to sequentially add new memories and integrate new knowledge. These limitations contrast with the human ability to continuously learn from new experiences and acquire knowledge throughout life. Most existing approaches add memories either through large context windows or external memory buffers (e.g., Retrieval-Augmented Generation), and studies on knowledge injection rarely test scenarios resembling everyday life events. In this work, we introduce a continual learning framework, Memory Embedded in Gated LLMs (MEGa), which injects event memories directly into the weights of LLMs. Each memory is stored in a dedicated set of gated low-rank weights. During inference, a gating mechanism activates relevant memory weights by matching query embeddings to stored memory embeddings. This enables the model to both recall entire memories and answer related questions. On two datasets - fictional characters and Wikipedia events - MEGa outperforms baseline approaches in mitigating catastrophic forgetting. Our model draws inspiration from the complementary memory system of the human brain.

Robust Learning in Bayesian Parallel Branching Graph Neural Networks: The Narrow Width Limit

The infinite width limit of random neural networks is known to result in Neural Networks as Gaussian Process (NNGP) (Lee et al. [2018]), characterized by task-independent kernels. It is widely accepted that larger network widths contribute to improved generalization (Park et al. [2019]). However, this work challenges this notion by investigating the narrow width limit of the Bayesian Parallel Branching Graph Neural Network (BPB-GNN), an architecture that resembles residual networks. We demonstrate that when the width of a BPB-GNN is significantly smaller compared to the number of training examples, each branch exhibits more robust learning due to a symmetry breaking of branches in kernel renormalization. Surprisingly, the performance of a BPB-GNN in the narrow width limit is generally superior or comparable to that achieved in the wide width limit in bias-limited scenarios. Furthermore, the readout norms of each branch in the narrow width limit are mostly independent of the architectural hyperparameters but generally reflective of the nature of the data. Our results characterize a newly defined narrow-width regime for parallel branching networks in general.

Self-supervised speech representation and contextual text embedding for match-mismatch classification with EEG recording

Relating speech to EEG holds considerable importance but is challenging. In this study, a deep convolutional network was employed to extract spatiotemporal features from EEG data. Self-supervised speech representation and contextual text embedding were used as speech features. Contrastive learning was used to relate EEG features to speech features. The experimental results demonstrate the benefits of using self-supervised speech representation and contextual text embedding. Through feature fusion and model ensemble, an accuracy of 60.29% was achieved, and the performance was ranked as No.2 in Task 1 of the Auditory EEG Challenge (ICASSP 2024). The code to implement our work is available on Github: https://github.com/bobwangPKU/EEG-Stimulus-Match-Mismatch.

ConvConcatNet: a deep convolutional neural network to reconstruct mel spectrogram from the EEG

To investigate the processing of speech in the brain, simple linear models are commonly used to establish a relationship between brain signals and speech features. However, these linear models are ill-equipped to model a highly dynamic and complex non-linear system like the brain. Although non-linear methods with neural networks have been developed recently, reconstructing unseen stimuli from unseen subjects' EEG is still a highly challenging task. This work presents a novel method, ConvConcatNet, to reconstruct mel-specgrams from EEG, in which the deep convolution neural network and extensive concatenation operation were combined. With our ConvConcatNet model, the Pearson correlation between the reconstructed and the target mel-spectrogram can achieve 0.0420, which was ranked as No.1 in the Task 2 of the Auditory EEG Challenge. The codes and models to implement our work will be available on Github: https://github.com/xuxiran/ConvConcatNet

Linear Latent World Models in Simple Transformers: A Case Study on Othello-GPT

Foundation models exhibit significant capabilities in decision-making and logical deductions. Nonetheless, a continuing discourse persists regarding their genuine understanding of the world as opposed to mere stochastic mimicry. This paper meticulously examines a simple transformer trained for Othello, extending prior research to enhance comprehension of the emergent world model of Othello-GPT. The investigation reveals that Othello-GPT encapsulates a linear representation of opposing pieces, a factor that causally steers its decision-making process. This paper further elucidates the interplay between the linear world representation and causal decision-making, and their dependence on layer depth and model complexity. We have made the code public.

Graph coarsening: From scientific computing to machine learning

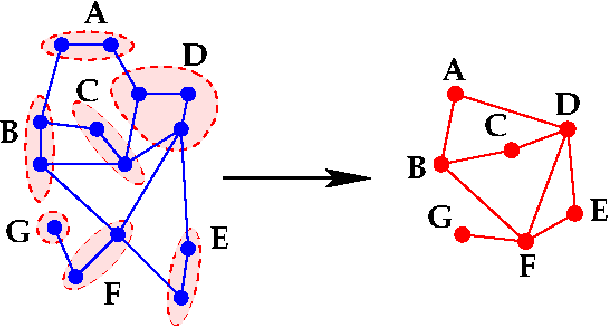
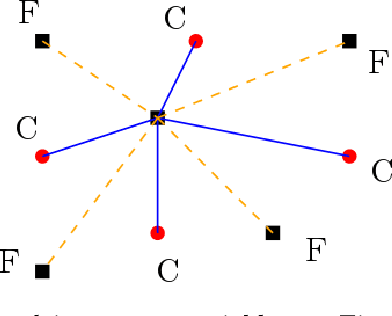
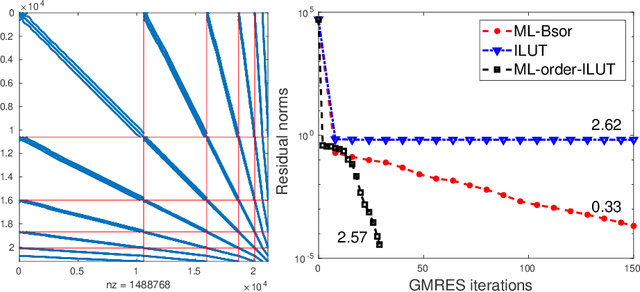
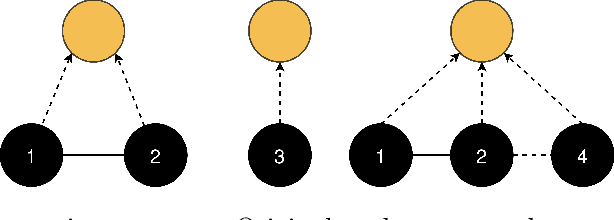
The general method of graph coarsening or graph reduction has been a remarkably useful and ubiquitous tool in scientific computing and it is now just starting to have a similar impact in machine learning. The goal of this paper is to take a broad look into coarsening techniques that have been successfully deployed in scientific computing and see how similar principles are finding their way in more recent applications related to machine learning. In scientific computing, coarsening plays a central role in algebraic multigrid methods as well as the related class of multilevel incomplete LU factorizations. In machine learning, graph coarsening goes under various names, e.g., graph downsampling or graph reduction. Its goal in most cases is to replace some original graph by one which has fewer nodes, but whose structure and characteristics are similar to those of the original graph. As will be seen, a common strategy in these methods is to rely on spectral properties to define the coarse graph.