Beyond Full Label: Single-Point Prompt for Infrared Small Target Label Generation

In this work, we make the first attempt to construct a learning-based single-point annotation paradigm for infrared small target label generation (IRSTLG). Our intuition is that label generation requires just one more point prompt than target detection: IRSTLG can be regarded as an infrared small target detection (IRSTD) task with the target location hint. Based on this insight, we introduce an energy double guided single-point prompt (EDGSP) framework, which adeptly transforms the target detection network into a refined label generation method. Specifically, the proposed EDGSP includes: 1) target energy initialization (TEI) to create a foundational outline for sufficient shape evolution of pseudo label, 2) double prompt embedding (DPE) for rapid localization of interested regions and reinforcement of individual differences to avoid label adhesion, and 3) bounding box-based matching (BBM) to eliminate false alarms. Experimental results show that pseudo labels generated by three baselines equipped with EDGSP achieve 100% object-level probability of detection (Pd) and 0% false-alarm rate (Fa) on SIRST, NUDT-SIRST, and IRSTD-1k datasets, with a pixel-level intersection over union (IoU) improvement of 13.28% over state-of-the-art label generation methods. Additionally, the downstream detection task reveals that our centroid-annotated pseudo labels surpass full labels, even with coarse single-point annotations, it still achieves 99.5% performance of full labeling.

A Guide to Image and Video based Small Object Detection using Deep Learning : Case Study of Maritime Surveillance

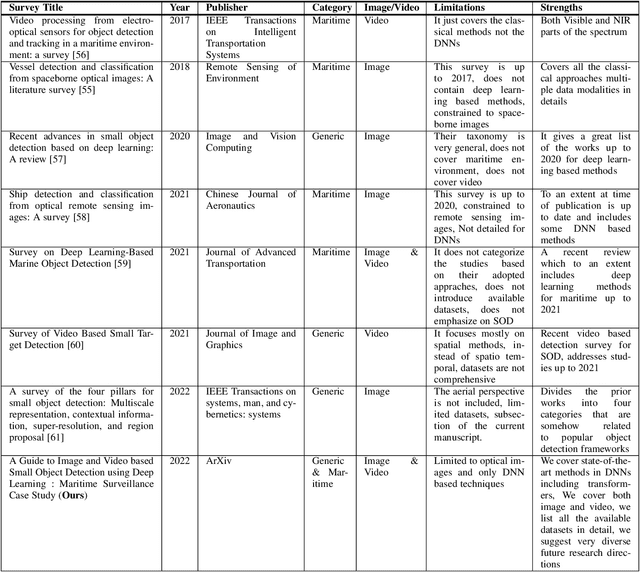
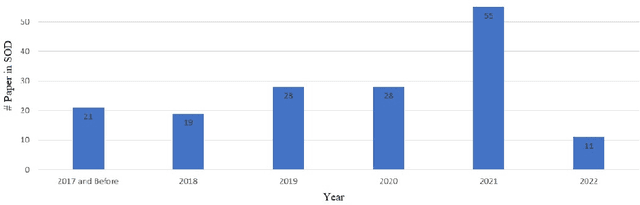
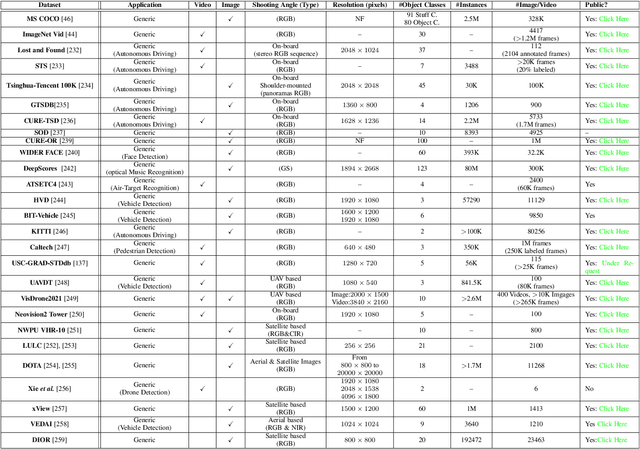
Small object detection (SOD) in optical images and videos is a challenging problem that even state-of-the-art generic object detection methods fail to accurately localize and identify such objects. Typically, small objects appear in real-world due to large camera-object distance. Because small objects occupy only a small area in the input image (e.g., less than 10%), the information extracted from such a small area is not always rich enough to support decision making. Multidisciplinary strategies are being developed by researchers working at the interface of deep learning and computer vision to enhance the performance of SOD deep learning based methods. In this paper, we provide a comprehensive review of over 160 research papers published between 2017 and 2022 in order to survey this growing subject. This paper summarizes the existing literature and provide a taxonomy that illustrates the broad picture of current research. We investigate how to improve the performance of small object detection in maritime environments, where increasing performance is critical. By establishing a connection between generic and maritime SOD research, future directions have been identified. In addition, the popular datasets that have been used for SOD for generic and maritime applications are discussed, and also well-known evaluation metrics for the state-of-the-art methods on some of the datasets are provided.

Find the dimension that counts: Fast dimension estimation and Krylov PCA

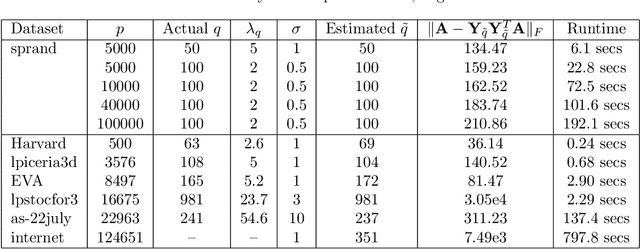
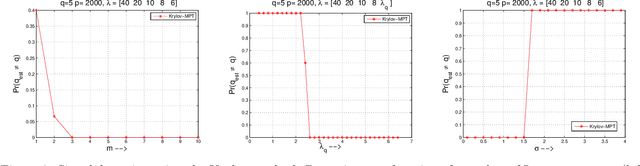
High dimensional data and systems with many degrees of freedom are often characterized by covariance matrices. In this paper, we consider the problem of simultaneously estimating the dimension of the principal (dominant) subspace of these covariance matrices and obtaining an approximation to the subspace. This problem arises in the popular principal component analysis (PCA), and in many applications of machine learning, data analysis, signal and image processing, and others. We first present a novel method for estimating the dimension of the principal subspace. We then show how this method can be coupled with a Krylov subspace method to simultaneously estimate the dimension and obtain an approximation to the subspace. The dimension estimation is achieved at no additional cost. The proposed method operates on a model selection framework, where the novel selection criterion is derived based on random matrix perturbation theory ideas. We present theoretical analyses which (a) show that the proposed method achieves strong consistency (i.e., yields optimal solution as the number of data-points $n\rightarrow \infty$), and (b) analyze conditions for exact dimension estimation in the finite $n$ case. Using recent results, we show that our algorithm also yields near optimal PCA. The proposed method avoids forming the sample covariance matrix (associated with the data) explicitly and computing the complete eigen-decomposition. Therefore, the method is inexpensive, which is particularly advantageous in modern data applications where the covariance matrices can be very large. Numerical experiments illustrate the performance of the proposed method in various applications.

Fast estimation of approximate matrix ranks using spectral densities

In many machine learning and data related applications, it is required to have the knowledge of approximate ranks of large data matrices at hand. In this paper, we present two computationally inexpensive techniques to estimate the approximate ranks of such large matrices. These techniques exploit approximate spectral densities, popular in physics, which are probability density distributions that measure the likelihood of finding eigenvalues of the matrix at a given point on the real line. Integrating the spectral density over an interval gives the eigenvalue count of the matrix in that interval. Therefore the rank can be approximated by integrating the spectral density over a carefully selected interval. Two different approaches are discussed to estimate the approximate rank, one based on Chebyshev polynomials and the other based on the Lanczos algorithm. In order to obtain the appropriate interval, it is necessary to locate a gap between the eigenvalues that correspond to noise and the relevant eigenvalues that contribute to the matrix rank. A method for locating this gap and selecting the interval of integration is proposed based on the plot of the spectral density. Numerical experiments illustrate the performance of these techniques on matrices from typical applications.