Find the dimension that counts: Fast dimension estimation and Krylov PCA
Paper and Code
Oct 08, 2018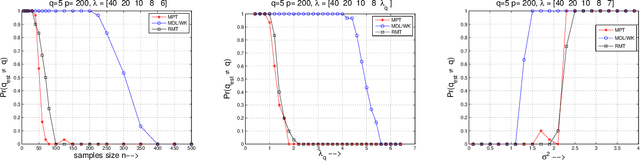
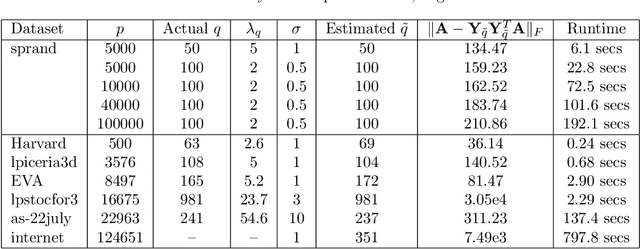

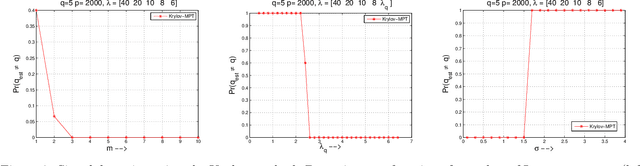
High dimensional data and systems with many degrees of freedom are often characterized by covariance matrices. In this paper, we consider the problem of simultaneously estimating the dimension of the principal (dominant) subspace of these covariance matrices and obtaining an approximation to the subspace. This problem arises in the popular principal component analysis (PCA), and in many applications of machine learning, data analysis, signal and image processing, and others. We first present a novel method for estimating the dimension of the principal subspace. We then show how this method can be coupled with a Krylov subspace method to simultaneously estimate the dimension and obtain an approximation to the subspace. The dimension estimation is achieved at no additional cost. The proposed method operates on a model selection framework, where the novel selection criterion is derived based on random matrix perturbation theory ideas. We present theoretical analyses which (a) show that the proposed method achieves strong consistency (i.e., yields optimal solution as the number of data-points $n\rightarrow \infty$), and (b) analyze conditions for exact dimension estimation in the finite $n$ case. Using recent results, we show that our algorithm also yields near optimal PCA. The proposed method avoids forming the sample covariance matrix (associated with the data) explicitly and computing the complete eigen-decomposition. Therefore, the method is inexpensive, which is particularly advantageous in modern data applications where the covariance matrices can be very large. Numerical experiments illustrate the performance of the proposed method in various applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge