Low rank approximation and decomposition of large matrices using error correcting codes
Paper and Code
Jun 15, 2017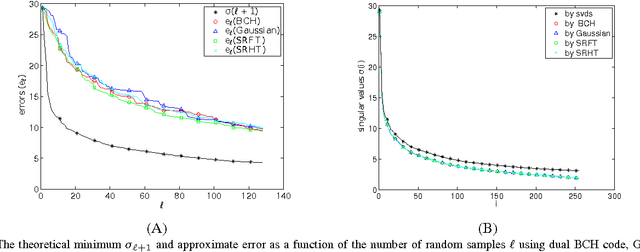
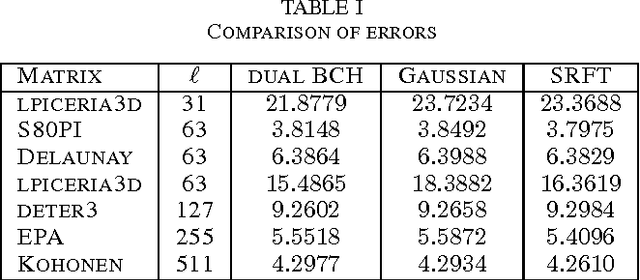
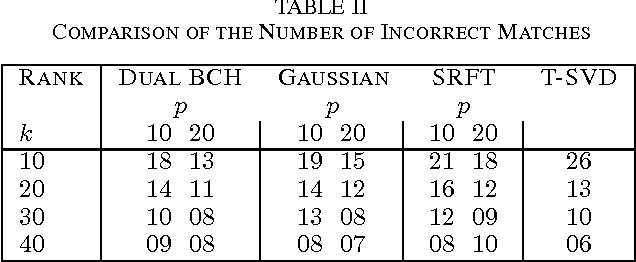
Low rank approximation is an important tool used in many applications of signal processing and machine learning. Recently, randomized sketching algorithms were proposed to effectively construct low rank approximations and obtain approximate singular value decompositions of large matrices. Similar ideas were used to solve least squares regression problems. In this paper, we show how matrices from error correcting codes can be used to find such low rank approximations and matrix decompositions, and extend the framework to linear least squares regression problems. The benefits of using these code matrices are the following: (i) They are easy to generate and they reduce randomness significantly. (ii) Code matrices with mild properties satisfy the subspace embedding property, and have a better chance of preserving the geometry of an entire subspace of vectors. (iii) For parallel and distributed applications, code matrices have significant advantages over structured random matrices and Gaussian random matrices. (iv) Unlike Fourier or Hadamard transform matrices, which require sampling $O(k\log k)$ columns for a rank-$k$ approximation, the log factor is not necessary for certain types of code matrices. That is, $(1+\epsilon)$ optimal Frobenius norm error can be achieved for a rank-$k$ approximation with $O(k/\epsilon)$ samples. (v) Fast multiplication is possible with structured code matrices, so fast approximations can be achieved for general dense input matrices. (vi) For least squares regression problem $\min\|Ax-b\|_2$ where $A\in \mathbb{R}^{n\times d}$, the $(1+\epsilon)$ relative error approximation can be achieved with $O(d/\epsilon)$ samples, with high probability, when certain code matrices are used.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge