RefLoRA: Refactored Low-Rank Adaptation for Efficient Fine-Tuning of Large Models

Low-Rank Adaptation (LoRA) lowers the computational and memory overhead of fine-tuning large models by updating a low-dimensional subspace of the pre-trained weight matrix. Albeit efficient, LoRA exhibits suboptimal convergence and noticeable performance degradation, due to inconsistent and imbalanced weight updates induced by its nonunique low-rank factorizations. To overcome these limitations, this article identifies the optimal low-rank factorization per step that minimizes an upper bound on the loss. The resultant refactored low-rank adaptation (RefLoRA) method promotes a flatter loss landscape, along with consistent and balanced weight updates, thus speeding up stable convergence. Extensive experiments evaluate RefLoRA on natural language understanding, and commonsense reasoning tasks with popular large language models including DeBERTaV3, LLaMA-7B, LLaMA2-7B and LLaMA3-8B. The numerical tests corroborate that RefLoRA converges faster, outperforms various benchmarks, and enjoys negligible computational overhead compared to state-of-the-art LoRA variants.

Preconditioned Sharpness-Aware Minimization: Unifying Analysis and a Novel Learning Algorithm

Targeting solutions over `flat' regions of the loss landscape, sharpness-aware minimization (SAM) has emerged as a powerful tool to improve generalizability of deep neural network based learning. While several SAM variants have been developed to this end, a unifying approach that also guides principled algorithm design has been elusive. This contribution leverages preconditioning (pre) to unify SAM variants and provide not only unifying convergence analysis, but also valuable insights. Building upon preSAM, a novel algorithm termed infoSAM is introduced to address the so-called adversarial model degradation issue in SAM by adjusting gradients depending on noise estimates. Extensive numerical tests demonstrate the superiority of infoSAM across various benchmarks.

Online scalable Gaussian processes with conformal prediction for guaranteed coverage

The Gaussian process (GP) is a Bayesian nonparametric paradigm that is widely adopted for uncertainty quantification (UQ) in a number of safety-critical applications, including robotics, healthcare, as well as surveillance. The consistency of the resulting uncertainty values however, hinges on the premise that the learning function conforms to the properties specified by the GP model, such as smoothness, periodicity and more, which may not be satisfied in practice, especially with data arriving on the fly. To combat against such model mis-specification, we propose to wed the GP with the prevailing conformal prediction (CP), a distribution-free post-processing framework that produces it prediction sets with a provably valid coverage under the sole assumption of data exchangeability. However, this assumption is usually violated in the online setting, where a prediction set is sought before revealing the true label. To ensure long-term coverage guarantee, we will adaptively set the key threshold parameter based on the feedback whether the true label falls inside the prediction set. Numerical results demonstrate the merits of the online GP-CP approach relative to existing alternatives in the long-term coverage performance.

Learning From Crowdsourced Noisy Labels: A Signal Processing Perspective

One of the primary catalysts fueling advances in artificial intelligence (AI) and machine learning (ML) is the availability of massive, curated datasets. A commonly used technique to curate such massive datasets is crowdsourcing, where data are dispatched to multiple annotators. The annotator-produced labels are then fused to serve downstream learning and inference tasks. This annotation process often creates noisy labels due to various reasons, such as the limited expertise, or unreliability of annotators, among others. Therefore, a core objective in crowdsourcing is to develop methods that effectively mitigate the negative impact of such label noise on learning tasks. This feature article introduces advances in learning from noisy crowdsourced labels. The focus is on key crowdsourcing models and their methodological treatments, from classical statistical models to recent deep learning-based approaches, emphasizing analytical insights and algorithmic developments. In particular, this article reviews the connections between signal processing (SP) theory and methods, such as identifiability of tensor and nonnegative matrix factorization, and novel, principled solutions of longstanding challenges in crowdsourcing -- showing how SP perspectives drive the advancements of this field. Furthermore, this article touches upon emerging topics that are critical for developing cutting-edge AI/ML systems, such as crowdsourcing in reinforcement learning with human feedback (RLHF) and direct preference optimization (DPO) that are key techniques for fine-tuning large language models (LLMs).

Meta-Learning with Versatile Loss Geometries for Fast Adaptation Using Mirror Descent

Utilizing task-invariant prior knowledge extracted from related tasks, meta-learning is a principled framework that empowers learning a new task especially when data records are limited. A fundamental challenge in meta-learning is how to quickly "adapt" the extracted prior in order to train a task-specific model within a few optimization steps. Existing approaches deal with this challenge using a preconditioner that enhances convergence of the per-task training process. Though effective in representing locally a quadratic training loss, these simple linear preconditioners can hardly capture complex loss geometries. The present contribution addresses this limitation by learning a nonlinear mirror map, which induces a versatile distance metric to enable capturing and optimizing a wide range of loss geometries, hence facilitating the per-task training. Numerical tests on few-shot learning datasets demonstrate the superior expressiveness and convergence of the advocated approach.

Contractive error feedback for gradient compression

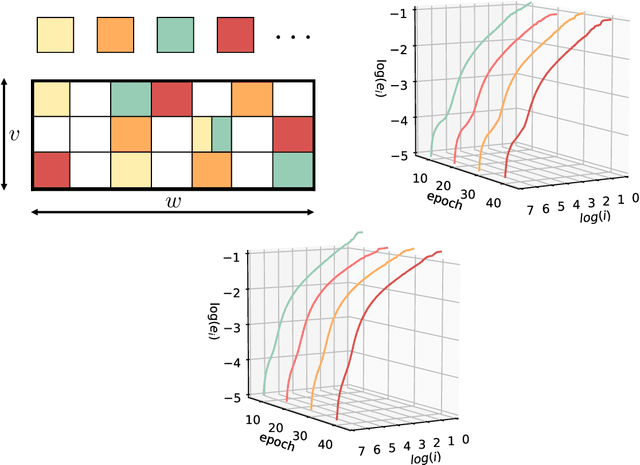
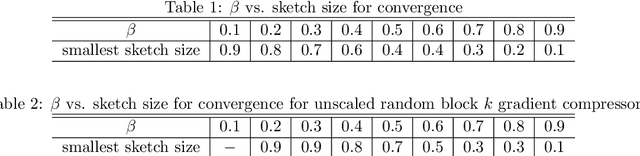
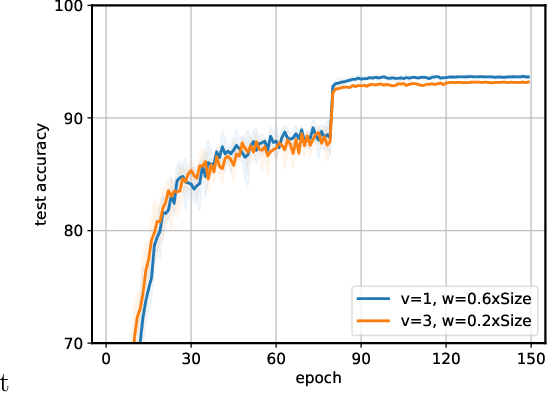
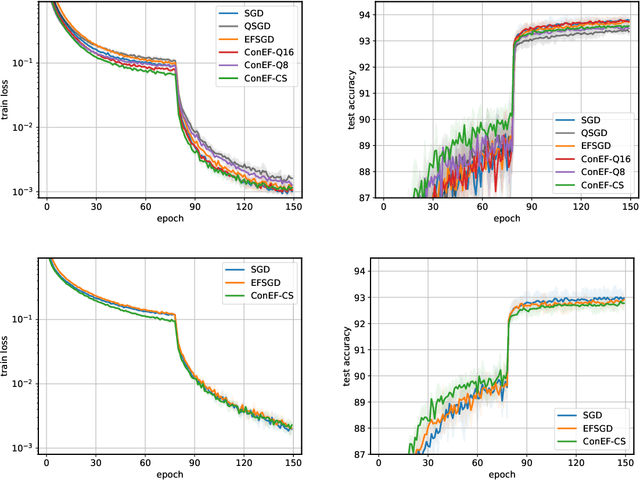
On-device memory concerns in distributed deep learning have become severe due to (i) the growth of model size in multi-GPU training, and (ii) the wide adoption of deep neural networks for federated learning on IoT devices which have limited storage. In such settings, communication efficient optimization methods are attractive alternatives, however they still struggle with memory issues. To tackle these challenges, we propose an communication efficient method called contractive error feedback (ConEF). As opposed to SGD with error-feedback (EFSGD) that inefficiently manages memory, ConEF obtains the sweet spot of convergence and memory usage, and achieves communication efficiency by leveraging biased and all-reducable gradient compression. We empirically validate ConEF on various learning tasks that include image classification, language modeling, and machine translation and observe that ConEF saves 80\% - 90\% of the extra memory in EFSGD with almost no loss on test performance, while also achieving 1.3x - 5x speedup of SGD. Through our work, we also demonstrate the feasibility and convergence of ConEF to clear up the theoretical barrier of integrating ConEF to popular memory efficient frameworks such as ZeRO-3.

3D Reconstruction in Noisy Agricultural Environments: A Bayesian Optimization Perspective for View Planning

3D reconstruction is a fundamental task in robotics that gained attention due to its major impact in a wide variety of practical settings, including agriculture, underwater, and urban environments. An important approach for this task, known as view planning, is to judiciously place a number of cameras in positions that maximize the visual information improving the resulting 3D reconstruction. Circumventing the need for a large number of arbitrary images, geometric criteria can be applied to select fewer yet more informative images to markedly improve the 3D reconstruction performance. Nonetheless, incorporating the noise of the environment that exists in various real-world scenarios into these criteria may be challenging, particularly when prior information about the noise is not provided. To that end, this work advocates a novel geometric function that accounts for the existing noise, relying solely on a relatively small number of noise realizations without requiring its closed-form expression. With no analytic expression of the geometric function, this work puts forth a Bayesian optimization algorithm for accurate 3D reconstruction in the presence of noise. Numerical tests on noisy agricultural environments showcase the impressive merits of the proposed approach for 3D reconstruction with even a small number of available cameras.

Enhancing Sharpness-Aware Optimization Through Variance Suppression

Sharpness-aware minimization (SAM) has well documented merits in enhancing generalization of deep neural networks, even without sizable data augmentation. Embracing the geometry of the loss function, where neighborhoods of 'flat minima' heighten generalization ability, SAM seeks 'flat valleys' by minimizing the maximum loss caused by an adversary perturbing parameters within the neighborhood. Although critical to account for sharpness of the loss function, such an 'over-friendly adversary' can curtail the outmost level of generalization. The novel approach of this contribution fosters stabilization of adversaries through variance suppression (VaSSO) to avoid such friendliness. VaSSO's provable stability safeguards its numerical improvement over SAM in model-agnostic tasks, including image classification and machine translation. In addition, experiments confirm that VaSSO endows SAM with robustness against high levels of label noise.

Conic Descent Redux for Memory-Efficient Optimization

Conic programming has well-documented merits in a gamut of signal processing and machine learning tasks. This contribution revisits a recently developed first-order conic descent (CD) solver, and advances it in three aspects: intuition, theory, and algorithmic implementation. It is found that CD can afford an intuitive geometric derivation that originates from the dual problem. This opens the door to novel algorithmic designs, with a momentum variant of CD, momentum conic descent (MOCO) exemplified. Diving deeper into the dual behavior CD and MOCO reveals: i) an analytically justified stopping criterion; and, ii) the potential to design preconditioners to speed up dual convergence. Lastly, to scale semidefinite programming (SDP) especially for low-rank solutions, a memory efficient MOCO variant is developed and numerically validated.

Scalable Bayesian Meta-Learning through Generalized Implicit Gradients

Meta-learning owns unique effectiveness and swiftness in tackling emerging tasks with limited data. Its broad applicability is revealed by viewing it as a bi-level optimization problem. The resultant algorithmic viewpoint however, faces scalability issues when the inner-level optimization relies on gradient-based iterations. Implicit differentiation has been considered to alleviate this challenge, but it is restricted to an isotropic Gaussian prior, and only favors deterministic meta-learning approaches. This work markedly mitigates the scalability bottleneck by cross-fertilizing the benefits of implicit differentiation to probabilistic Bayesian meta-learning. The novel implicit Bayesian meta-learning (iBaML) method not only broadens the scope of learnable priors, but also quantifies the associated uncertainty. Furthermore, the ultimate complexity is well controlled regardless of the inner-level optimization trajectory. Analytical error bounds are established to demonstrate the precision and efficiency of the generalized implicit gradient over the explicit one. Extensive numerical tests are also carried out to empirically validate the performance of the proposed method.