Zeroth-Order Optimization Finds Flat Minima

Zeroth-order methods are extensively used in machine learning applications where gradients are infeasible or expensive to compute, such as black-box attacks, reinforcement learning, and language model fine-tuning. Existing optimization theory focuses on convergence to an arbitrary stationary point, but less is known on the implicit regularization that provides a fine-grained characterization on which particular solutions are finally reached. We show that zeroth-order optimization with the standard two-point estimator favors solutions with small trace of Hessian, which is widely used in previous work to distinguish between sharp and flat minima. We further provide convergence rates of zeroth-order optimization to approximate flat minima for convex and sufficiently smooth functions, where flat minima are defined as the minimizers that achieve the smallest trace of Hessian among all optimal solutions. Experiments on binary classification tasks with convex losses and language model fine-tuning support our theoretical findings.

RefLoRA: Refactored Low-Rank Adaptation for Efficient Fine-Tuning of Large Models

Low-Rank Adaptation (LoRA) lowers the computational and memory overhead of fine-tuning large models by updating a low-dimensional subspace of the pre-trained weight matrix. Albeit efficient, LoRA exhibits suboptimal convergence and noticeable performance degradation, due to inconsistent and imbalanced weight updates induced by its nonunique low-rank factorizations. To overcome these limitations, this article identifies the optimal low-rank factorization per step that minimizes an upper bound on the loss. The resultant refactored low-rank adaptation (RefLoRA) method promotes a flatter loss landscape, along with consistent and balanced weight updates, thus speeding up stable convergence. Extensive experiments evaluate RefLoRA on natural language understanding, and commonsense reasoning tasks with popular large language models including DeBERTaV3, LLaMA-7B, LLaMA2-7B and LLaMA3-8B. The numerical tests corroborate that RefLoRA converges faster, outperforms various benchmarks, and enjoys negligible computational overhead compared to state-of-the-art LoRA variants.

Can RLHF be More Efficient with Imperfect Reward Models? A Policy Coverage Perspective

Sample efficiency is critical for online Reinforcement Learning from Human Feedback (RLHF). While existing works investigate sample-efficient online exploration strategies, the potential of utilizing misspecified yet relevant reward models to accelerate learning remains underexplored. This paper studies how to transfer knowledge from those imperfect reward models in online RLHF. We start by identifying a novel property of the KL-regularized RLHF objective: \emph{a policy's ability to cover the optimal policy is captured by its sub-optimality}. Building on this insight, we propose a theoretical transfer learning algorithm with provable benefits compared to standard online learning. Our approach achieves low regret in the early stage by quickly adapting to the best available source reward models without prior knowledge of their quality, and over time, it attains an $\tilde{O}(\sqrt{T})$ regret bound \emph{independent} of structural complexity measures. Inspired by our theoretical findings, we develop an empirical algorithm with improved computational efficiency, and demonstrate its effectiveness empirically in summarization tasks.

Preconditioned Sharpness-Aware Minimization: Unifying Analysis and a Novel Learning Algorithm

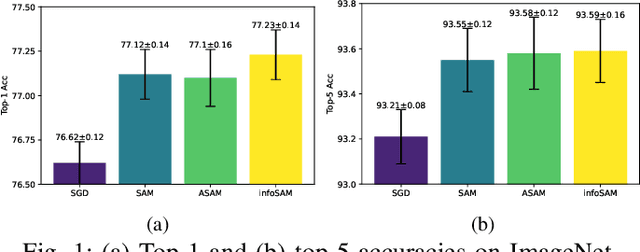
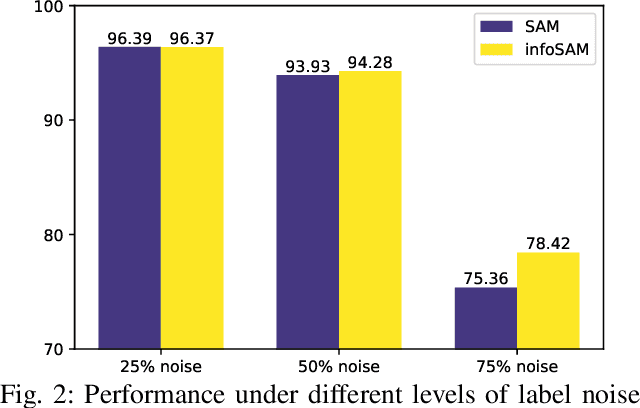
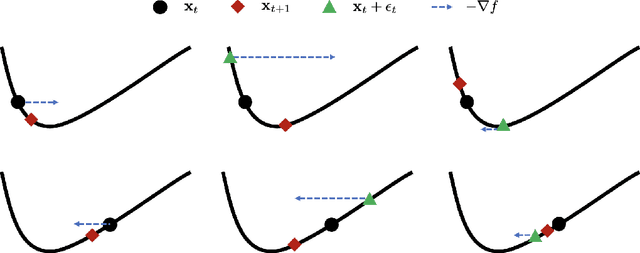
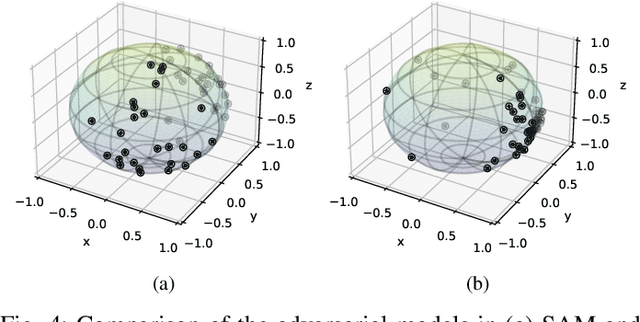
Targeting solutions over `flat' regions of the loss landscape, sharpness-aware minimization (SAM) has emerged as a powerful tool to improve generalizability of deep neural network based learning. While several SAM variants have been developed to this end, a unifying approach that also guides principled algorithm design has been elusive. This contribution leverages preconditioning (pre) to unify SAM variants and provide not only unifying convergence analysis, but also valuable insights. Building upon preSAM, a novel algorithm termed infoSAM is introduced to address the so-called adversarial model degradation issue in SAM by adjusting gradients depending on noise estimates. Extensive numerical tests demonstrate the superiority of infoSAM across various benchmarks.

On the Crucial Role of Initialization for Matrix Factorization

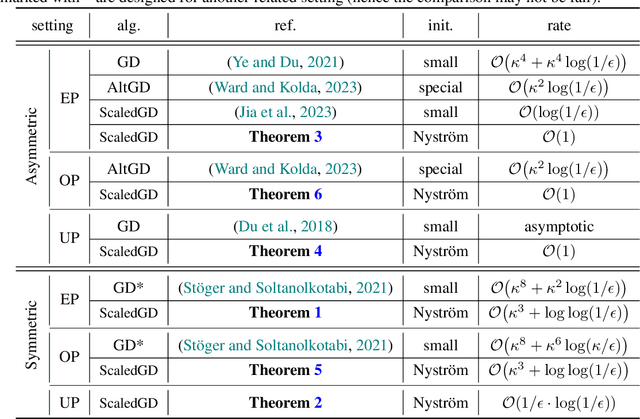
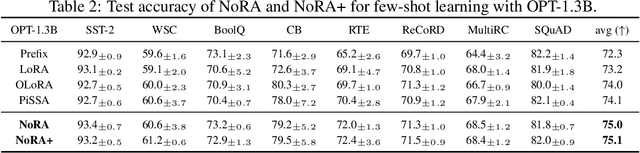
This work revisits the classical low-rank matrix factorization problem and unveils the critical role of initialization in shaping convergence rates for such nonconvex and nonsmooth optimization. We introduce Nystrom initialization, which significantly improves the global convergence of Scaled Gradient Descent (ScaledGD) in both symmetric and asymmetric matrix factorization tasks. Specifically, we prove that ScaledGD with Nystrom initialization achieves quadratic convergence in cases where only linear rates were previously known. Furthermore, we extend this initialization to low-rank adapters (LoRA) commonly used for finetuning foundation models. Our approach, NoRA, i.e., LoRA with Nystrom initialization, demonstrates superior performance across various downstream tasks and model scales, from 1B to 7B parameters, in large language and diffusion models.

Implicit Regularization of Sharpness-Aware Minimization for Scale-Invariant Problems

Sharpness-aware minimization (SAM) improves generalization of various deep learning tasks. Motivated by popular architectures such as LoRA, we explore the implicit regularization of SAM for scale-invariant problems involving two groups of variables. Instead of focusing on commonly used sharpness, this work introduces a concept termed balancedness, defined as the difference between the squared norm of two variables. This allows us to depict richer global behaviors of SAM. In particular, our theoretical and empirical findings reveal that i) SAM promotes balancedness; and ii) the regularization on balancedness is data-responsive -- outliers have stronger impact. The latter coincides with empirical observations that SAM outperforms SGD in the presence of outliers. Leveraging the implicit regularization, we develop a resource-efficient SAM variant, balancedness-aware regularization (BAR), tailored for scale-invariant problems such as finetuning language models with LoRA. BAR saves 95% computational overhead of SAM, with enhanced test performance across various tasks on RoBERTa, GPT2, and OPT-1.3B.

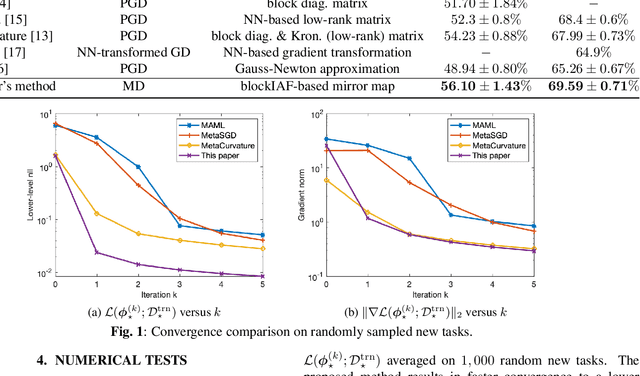
Meta-Learning with Versatile Loss Geometries for Fast Adaptation Using Mirror Descent

Utilizing task-invariant prior knowledge extracted from related tasks, meta-learning is a principled framework that empowers learning a new task especially when data records are limited. A fundamental challenge in meta-learning is how to quickly "adapt" the extracted prior in order to train a task-specific model within a few optimization steps. Existing approaches deal with this challenge using a preconditioner that enhances convergence of the per-task training process. Though effective in representing locally a quadratic training loss, these simple linear preconditioners can hardly capture complex loss geometries. The present contribution addresses this limitation by learning a nonlinear mirror map, which induces a versatile distance metric to enable capturing and optimizing a wide range of loss geometries, hence facilitating the per-task training. Numerical tests on few-shot learning datasets demonstrate the superior expressiveness and convergence of the advocated approach.

Contractive error feedback for gradient compression

On-device memory concerns in distributed deep learning have become severe due to (i) the growth of model size in multi-GPU training, and (ii) the wide adoption of deep neural networks for federated learning on IoT devices which have limited storage. In such settings, communication efficient optimization methods are attractive alternatives, however they still struggle with memory issues. To tackle these challenges, we propose an communication efficient method called contractive error feedback (ConEF). As opposed to SGD with error-feedback (EFSGD) that inefficiently manages memory, ConEF obtains the sweet spot of convergence and memory usage, and achieves communication efficiency by leveraging biased and all-reducable gradient compression. We empirically validate ConEF on various learning tasks that include image classification, language modeling, and machine translation and observe that ConEF saves 80\% - 90\% of the extra memory in EFSGD with almost no loss on test performance, while also achieving 1.3x - 5x speedup of SGD. Through our work, we also demonstrate the feasibility and convergence of ConEF to clear up the theoretical barrier of integrating ConEF to popular memory efficient frameworks such as ZeRO-3.

Enhancing Sharpness-Aware Optimization Through Variance Suppression

Sharpness-aware minimization (SAM) has well documented merits in enhancing generalization of deep neural networks, even without sizable data augmentation. Embracing the geometry of the loss function, where neighborhoods of 'flat minima' heighten generalization ability, SAM seeks 'flat valleys' by minimizing the maximum loss caused by an adversary perturbing parameters within the neighborhood. Although critical to account for sharpness of the loss function, such an 'over-friendly adversary' can curtail the outmost level of generalization. The novel approach of this contribution fosters stabilization of adversaries through variance suppression (VaSSO) to avoid such friendliness. VaSSO's provable stability safeguards its numerical improvement over SAM in model-agnostic tasks, including image classification and machine translation. In addition, experiments confirm that VaSSO endows SAM with robustness against high levels of label noise.

Conic Descent Redux for Memory-Efficient Optimization

Conic programming has well-documented merits in a gamut of signal processing and machine learning tasks. This contribution revisits a recently developed first-order conic descent (CD) solver, and advances it in three aspects: intuition, theory, and algorithmic implementation. It is found that CD can afford an intuitive geometric derivation that originates from the dual problem. This opens the door to novel algorithmic designs, with a momentum variant of CD, momentum conic descent (MOCO) exemplified. Diving deeper into the dual behavior CD and MOCO reveals: i) an analytically justified stopping criterion; and, ii) the potential to design preconditioners to speed up dual convergence. Lastly, to scale semidefinite programming (SDP) especially for low-rank solutions, a memory efficient MOCO variant is developed and numerically validated.