Mitigating Preference Hacking in Policy Optimization with Pessimism

This work tackles the problem of overoptimization in reinforcement learning from human feedback (RLHF), a prevalent technique for aligning models with human preferences. RLHF relies on reward or preference models trained on \emph{fixed preference datasets}, and these models are unreliable when evaluated outside the support of this preference data, leading to the common reward or preference hacking phenomenon. We propose novel, pessimistic objectives for RLHF which are provably robust to overoptimization through the use of pessimism in the face of uncertainty, and design practical algorithms, P3O and PRPO, to optimize these objectives. Our approach is derived for the general preference optimization setting, but can be used with reward models as well. We evaluate P3O and PRPO on the tasks of fine-tuning language models for document summarization and creating helpful assistants, demonstrating remarkable resilience to overoptimization.

Can RLHF be More Efficient with Imperfect Reward Models? A Policy Coverage Perspective

Sample efficiency is critical for online Reinforcement Learning from Human Feedback (RLHF). While existing works investigate sample-efficient online exploration strategies, the potential of utilizing misspecified yet relevant reward models to accelerate learning remains underexplored. This paper studies how to transfer knowledge from those imperfect reward models in online RLHF. We start by identifying a novel property of the KL-regularized RLHF objective: \emph{a policy's ability to cover the optimal policy is captured by its sub-optimality}. Building on this insight, we propose a theoretical transfer learning algorithm with provable benefits compared to standard online learning. Our approach achieves low regret in the early stage by quickly adapting to the best available source reward models without prior knowledge of their quality, and over time, it attains an $\tilde{O}(\sqrt{T})$ regret bound \emph{independent} of structural complexity measures. Inspired by our theoretical findings, we develop an empirical algorithm with improved computational efficiency, and demonstrate its effectiveness empirically in summarization tasks.

Design Considerations in Offline Preference-based RL

Offline algorithms for Reinforcement Learning from Human Preferences (RLHF), which use only a fixed dataset of sampled responses given an input, and preference feedback among these responses, have gained increasing prominence in the literature on aligning language models. In this paper, we study how the different design choices made in methods such as DPO, IPO, SLiC and many variants influence the quality of the learned policy, from a theoretical perspective. Our treatment yields insights into the choices of loss function, the policy which is used to normalize log-likelihoods, and also the role of the data sampling policy. Notably, our results do not rely on the standard reparameterization-style arguments used to motivate some of the algorithms in this family, which allows us to give a unified treatment to a broad class of methods. We also conduct a small empirical study to verify some of the theoretical findings on a standard summarization benchmark.

Preserving Expert-Level Privacy in Offline Reinforcement Learning

The offline reinforcement learning (RL) problem aims to learn an optimal policy from historical data collected by one or more behavioural policies (experts) by interacting with an environment. However, the individual experts may be privacy-sensitive in that the learnt policy may retain information about their precise choices. In some domains like personalized retrieval, advertising and healthcare, the expert choices are considered sensitive data. To provably protect the privacy of such experts, we propose a novel consensus-based expert-level differentially private offline RL training approach compatible with any existing offline RL algorithm. We prove rigorous differential privacy guarantees, while maintaining strong empirical performance. Unlike existing work in differentially private RL, we supplement the theory with proof-of-concept experiments on classic RL environments featuring large continuous state spaces, demonstrating substantial improvements over a natural baseline across multiple tasks.

Conditioned Language Policy: A General Framework for Steerable Multi-Objective Finetuning

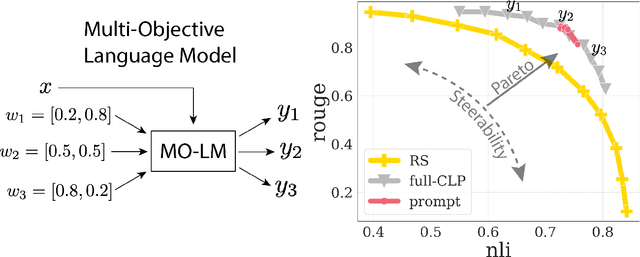
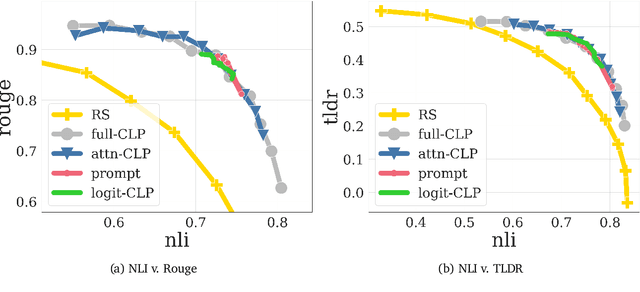
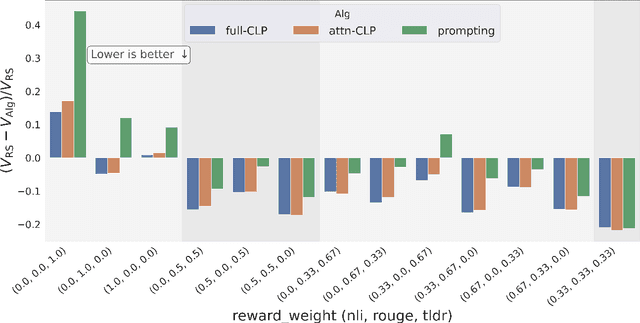
Reward-based finetuning is crucial for aligning language policies with intended behaviors (e.g., creativity and safety). A key challenge here is to develop steerable language models that trade-off multiple (conflicting) objectives in a flexible and efficient manner. This paper presents Conditioned Language Policy (CLP), a general framework for finetuning language models on multiple objectives. Building on techniques from multi-task training and parameter-efficient finetuning, CLP can learn steerable models that effectively trade-off conflicting objectives at inference time. Notably, this does not require training or maintaining multiple models to achieve different trade-offs between the objectives. Through an extensive set of experiments and ablations, we show that the CLP framework learns steerable models that outperform and Pareto-dominate the current state-of-the-art approaches for multi-objective finetuning.

Rate-Preserving Reductions for Blackwell Approachability

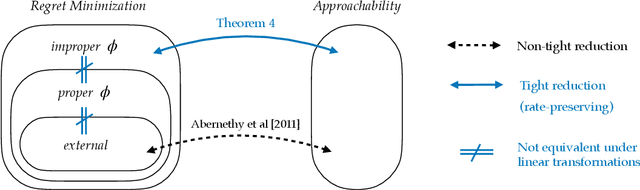
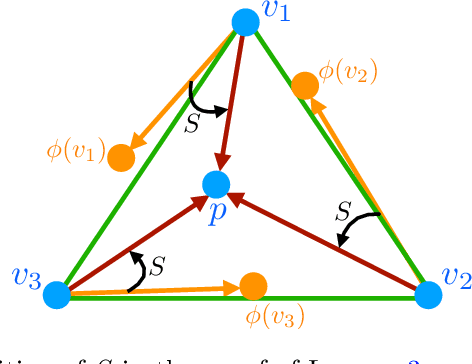
Abernethy et al. (2011) showed that Blackwell approachability and no-regret learning are equivalent, in the sense that any algorithm that solves a specific Blackwell approachability instance can be converted to a sublinear regret algorithm for a specific no-regret learning instance, and vice versa. In this paper, we study a more fine-grained form of such reductions, and ask when this translation between problems preserves not only a sublinear rate of convergence, but also preserves the optimal rate of convergence. That is, in which cases does it suffice to find the optimal regret bound for a no-regret learning instance in order to find the optimal rate of convergence for a corresponding approachability instance? We show that the reduction of Abernethy et al. (2011) does not preserve rates: their reduction may reduce a $d$-dimensional approachability instance $I_1$ with optimal convergence rate $R_1$ to a no-regret learning instance $I_2$ with optimal regret-per-round of $R_2$, with $R_{2}/R_{1}$ arbitrarily large (in particular, it is possible that $R_1 = 0$ and $R_{2} > 0$). On the other hand, we show that it is possible to tightly reduce any approachability instance to an instance of a generalized form of regret minimization we call improper $\phi$-regret minimization (a variant of the $\phi$-regret minimization of Gordon et al. (2008) where the transformation functions may map actions outside of the action set). Finally, we characterize when linear transformations suffice to reduce improper $\phi$-regret minimization problems to standard classes of regret minimization problems in a rate preserving manner. We prove that some improper $\phi$-regret minimization instances cannot be reduced to either subclass of instance in this way, suggesting that approachability can capture some problems that cannot be phrased in the language of online learning.

A Minimaximalist Approach to Reinforcement Learning from Human Feedback

We present Self-Play Preference Optimization (SPO), an algorithm for reinforcement learning from human feedback. Our approach is minimalist in that it does not require training a reward model nor unstable adversarial training and is therefore rather simple to implement. Our approach is maximalist in that it provably handles non-Markovian, intransitive, and stochastic preferences while being robust to the compounding errors that plague offline approaches to sequential prediction. To achieve the preceding qualities, we build upon the concept of a Minimax Winner (MW), a notion of preference aggregation from the social choice theory literature that frames learning from preferences as a zero-sum game between two policies. By leveraging the symmetry of this game, we prove that rather than using the traditional technique of dueling two policies to compute the MW, we can simply have a single agent play against itself while maintaining strong convergence guarantees. Practically, this corresponds to sampling multiple trajectories from a policy, asking a rater or preference model to compare them, and then using the proportion of wins as the reward for a particular trajectory. We demonstrate that on a suite of continuous control tasks, we are able to learn significantly more efficiently than reward-model based approaches while maintaining robustness to the intransitive and stochastic preferences that frequently occur in practice when aggregating human judgments.

Data-Driven Regret Balancing for Online Model Selection in Bandits

We consider model selection for sequential decision making in stochastic environments with bandit feedback, where a meta-learner has at its disposal a pool of base learners, and decides on the fly which action to take based on the policies recommended by each base learner. Model selection is performed by regret balancing but, unlike the recent literature on this subject, we do not assume any prior knowledge about the base learners like candidate regret guarantees; instead, we uncover these quantities in a data-driven manner. The meta-learner is therefore able to leverage the realized regret incurred by each base learner for the learning environment at hand (as opposed to the expected regret), and single out the best such regret. We design two model selection algorithms operating with this more ambitious notion of regret and, besides proving model selection guarantees via regret balancing, we experimentally demonstrate the compelling practical benefits of dealing with actual regrets instead of candidate regret bounds.

A Blackbox Approach to Best of Both Worlds in Bandits and Beyond

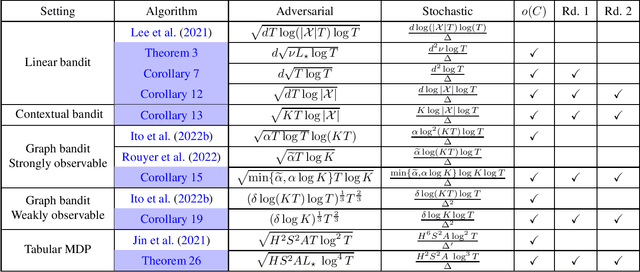
Best-of-both-worlds algorithms for online learning which achieve near-optimal regret in both the adversarial and the stochastic regimes have received growing attention recently. Existing techniques often require careful adaptation to every new problem setup, including specialised potentials and careful tuning of algorithm parameters. Yet, in domains such as linear bandits, it is still unknown if there exists an algorithm that can simultaneously obtain $O(\log(T))$ regret in the stochastic regime and $\tilde{O}(\sqrt{T})$ regret in the adversarial regime. In this work, we resolve this question positively and present a general reduction from best of both worlds to a wide family of follow-the-regularized-leader (FTRL) and online-mirror-descent (OMD) algorithms. We showcase the capability of this reduction by transforming existing algorithms that are only known to achieve worst-case guarantees into new algorithms with best-of-both-worlds guarantees in contextual bandits, graph bandits and tabular Markov decision processes.

Best of Both Worlds Policy Optimization

Policy optimization methods are popular reinforcement learning algorithms in practice. Recent works have built theoretical foundation for them by proving $\sqrt{T}$ regret bounds even when the losses are adversarial. Such bounds are tight in the worst case but often overly pessimistic. In this work, we show that in tabular Markov decision processes (MDPs), by properly designing the regularizer, the exploration bonus and the learning rates, one can achieve a more favorable polylog$(T)$ regret when the losses are stochastic, without sacrificing the worst-case guarantee in the adversarial regime. To our knowledge, this is also the first time a gap-dependent polylog$(T)$ regret bound is shown for policy optimization. Specifically, we achieve this by leveraging a Tsallis entropy or a Shannon entropy regularizer in the policy update. Then we show that under known transitions, we can further obtain a first-order regret bound in the adversarial regime by leveraging the log-barrier regularizer.