A Theoretical Framework for Modular Learning of Robust Generative Models

Training large-scale generative models is resource-intensive and relies heavily on heuristic dataset weighting. We address two fundamental questions: Can we train Large Language Models (LLMs) modularly-combining small, domain-specific experts to match monolithic performance-and can we do so robustly for any data mixture, eliminating heuristic tuning? We present a theoretical framework for modular generative modeling where a set of pre-trained experts are combined via a gating mechanism. We define the space of normalized gating functions, $G_{1}$, and formulate the problem as a minimax game to find a single robust gate that minimizes divergence to the worst-case data mixture. We prove the existence of such a robust gate using Kakutani's fixed-point theorem and show that modularity acts as a strong regularizer, with generalization bounds scaling with the lightweight gate's complexity. Furthermore, we prove that this modular approach can theoretically outperform models retrained on aggregate data, with the gap characterized by the Jensen-Shannon Divergence. Finally, we introduce a scalable Stochastic Primal-Dual algorithm and a Structural Distillation method for efficient inference. Empirical results on synthetic and real-world datasets confirm that our modular architecture effectively mitigates gradient conflict and can robustly outperform monolithic baselines.

Temper-Then-Tilt: Principled Unlearning for Generative Models through Tempering and Classifier Guidance

We study machine unlearning in large generative models by framing the task as density ratio estimation to a target distribution rather than supervised fine-tuning. While classifier guidance is a standard approach for approximating this ratio and can succeed in general, we show it can fail to faithfully unlearn with finite samples when the forget set represents a sharp, concentrated data distribution. To address this, we introduce Temper-Then-Tilt Unlearning (T3-Unlearning), which freezes the base model and applies a two-step inference procedure: (i) tempering the base distribution to flatten high-confidence spikes, and (ii) tilting the tempered distribution using a lightweight classifier trained to distinguish retain from forget samples. Our theoretical analysis provides finite-sample guarantees linking the surrogate classifier's risk to unlearning error, proving that tempering is necessary to successfully unlearn for concentrated distributions. Empirical evaluations on the TOFU benchmark show that T3-Unlearning improves forget quality and generative utility over existing baselines, while training only a fraction of the parameters with a minimal runtime.

Adaptive Matrix Online Learning through Smoothing with Guarantees for Nonsmooth Nonconvex Optimization

We study online linear optimization with matrix variables constrained by the operator norm, a setting where the geometry renders designing data-dependent and efficient adaptive algorithms challenging. The best-known adaptive regret bounds are achieved by Shampoo-like methods, but they require solving a costly quadratic projection subproblem. To address this, we extend the gradient-based prediction scheme to adaptive matrix online learning and cast algorithm design as constructing a family of smoothed potentials for the nuclear norm. We define a notion of admissibility for such smoothings and prove any admissible smoothing yields a regret bound matching the best-known guarantees of one-sided Shampoo. We instantiate this framework with two efficient methods that avoid quadratic projections. The first is an adaptive Follow-the-Perturbed-Leader (FTPL) method using Gaussian stochastic smoothing. The second is Follow-the-Augmented-Matrix-Leader (FAML), which uses a deterministic hyperbolic smoothing in an augmented matrix space. By analyzing the admissibility of these smoothings, we show both methods admit closed-form updates and match one-sided Shampoo's regret up to a constant factor, while significantly reducing computational cost. Lastly, using the online-to-nonconvex conversion, we derive two matrix-based optimizers, Pion (from FTPL) and Leon (from FAML). We prove convergence guarantees for these methods in nonsmooth nonconvex settings, a guarantee that the popular Muon optimizer lacks.

Rational Transductors

Standard Transformers excel at semantic modeling but struggle with rigid sequential logic and state tracking. Theoretical work establishes that self-attention is limited to $\AC^0$ (under hard attention) or $\TC^0$ (under soft attention), complexity classes that often fail to support robust length generalization on sequential problems without intermediate chain-of-thought. In this work, we introduce \emph{Rational Transductors}, a dual-stream architecture that augments the Transformer with a matrix-valued recurrence derived from Weighted Finite Automata (WFA). By injecting rational state information into the attention mechanism via a \emph{Deep Rational Injection} scheme, our framework strictly generalizes the expressive power of Transformers to capture all Regular Languages, $\NC^1$-complete problems (such as Boolean Formula Evaluation), and fundamental separations like Parity and Modular Counting, while preserving $O(L + \log T)$ parallel time complexity. We ground the architecture in a rigorous learning theory: we prove that \emph{Random Rational Features} act as a universal basis for sequential dependencies, justifying our initialization strategy, while establishing that the \emph{Differentiable Rational Feature} regime is necessary to close the representational compactness gap. Theoretical analysis and empirical results demonstrate that Rational Transductors solve the "Regular Gap," enabling robust length generalization on algorithmic tasks where standard Transformers fail, without the sequential computational bottlenecks of traditional RNNs.

Improved Balanced Classification with Theoretically Grounded Loss Functions

The balanced loss is a widely adopted objective for multi-class classification under class imbalance. By assigning equal importance to all classes, regardless of their frequency, it promotes fairness and ensures that minority classes are not overlooked. However, directly minimizing the balanced classification loss is typically intractable, which makes the design of effective surrogate losses a central question. This paper introduces and studies two advanced surrogate loss families: Generalized Logit-Adjusted (GLA) loss functions and Generalized Class-Aware weighted (GCA) losses. GLA losses generalize Logit-Adjusted losses, which shift logits based on class priors, to the broader general cross-entropy loss family. GCA loss functions extend the standard class-weighted losses, which scale losses inversely by class frequency, by incorporating class-dependent confidence margins and extending them to the general cross-entropy family. We present a comprehensive theoretical analysis of consistency for both loss families. We show that GLA losses are Bayes-consistent, but only $H$-consistent for complete (i.e., unbounded) hypothesis sets. Moreover, their $H$-consistency bounds depend inversely on the minimum class probability, scaling at least as $1/\mathsf p_{\min}$. In contrast, GCA losses are $H$-consistent for any hypothesis set that is bounded or complete, with $H$-consistency bounds that scale more favorably as $1/\sqrt{\mathsf p_{\min}}$, offering significantly stronger theoretical guarantees in imbalanced settings. We report the results of experiments demonstrating that, empirically, both the GCA losses with calibrated class-dependent confidence margins and GLA losses can greatly outperform straightforward class-weighted losses as well as the LA losses. GLA generally performs slightly better in common benchmarks, whereas GCA exhibits a slight edge in highly imbalanced settings.

Principled Algorithms for Optimizing Generalized Metrics in Binary Classification

In applications with significant class imbalance or asymmetric costs, metrics such as the $F_β$-measure, AM measure, Jaccard similarity coefficient, and weighted accuracy offer more suitable evaluation criteria than standard binary classification loss. However, optimizing these metrics present significant computational and statistical challenges. Existing approaches often rely on the characterization of the Bayes-optimal classifier, and use threshold-based methods that first estimate class probabilities and then seek an optimal threshold. This leads to algorithms that are not tailored to restricted hypothesis sets and lack finite-sample performance guarantees. In this work, we introduce principled algorithms for optimizing generalized metrics, supported by $H$-consistency and finite-sample generalization bounds. Our approach reformulates metric optimization as a generalized cost-sensitive learning problem, enabling the design of novel surrogate loss functions with provable $H$-consistency guarantees. Leveraging this framework, we develop new algorithms, METRO (Metric Optimization), with strong theoretical performance guarantees. We report the results of experiments demonstrating the effectiveness of our methods compared to prior baselines.

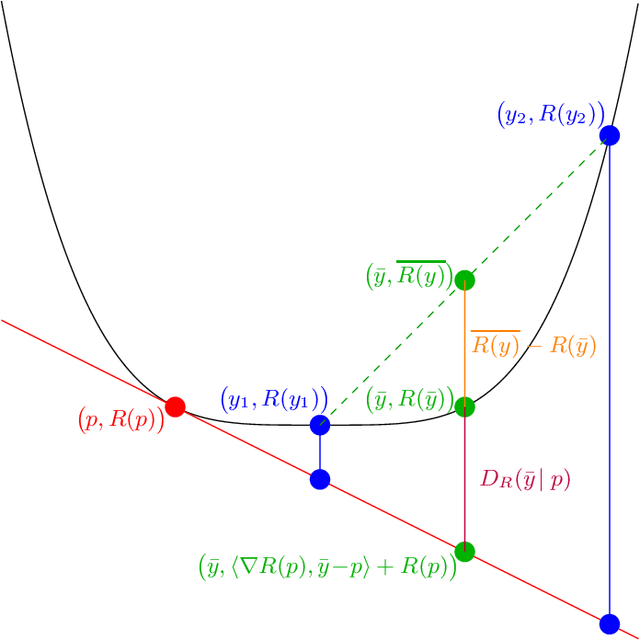
Coherence Mechanisms for Provable Self-Improvement

Self-improvement is a critical capability for large language models and other intelligent systems, enabling them to refine their behavior and internal consistency without external supervision. Despite its importance, prior approaches largely rely on empirical heuristics and lack formal guarantees. In this paper, we propose a principled framework for self-improvement based on the concept of \emph{coherence}, which requires that a model's outputs remain consistent under task-preserving transformations of the input. We formalize this concept using projection-based mechanisms that update a baseline model to be coherent while remaining as close as possible to its original behavior. We provide rigorous theoretical guarantees that these mechanisms achieve \emph{monotonic improvement}, measured by a reduction in expected Bregman divergence. Our analysis is comprehensive, covering both \emph{direct} and \emph{two-step} projection methods, and robustly extends these guarantees to non-realizable settings, empirical (finite-sample) distributions, and relaxed coherence constraints. Furthermore, we establish a general \emph{characterization theorem}, showing that any mechanism with similar provable improvement guarantees must inherently conform to a coherence-based structure. This culminates in rigidity results under the demand for universal improvement, establishing coherence as a fundamental and, in a formal sense, necessary principle for provable self-improvement.

Budgeted Multiple-Expert Deferral

Learning to defer uncertain predictions to costly experts offers a powerful strategy for improving the accuracy and efficiency of machine learning systems. However, standard training procedures for deferral algorithms typically require querying all experts for every training instance, an approach that becomes prohibitively expensive when expert queries incur significant computational or resource costs. This undermines the core goal of deferral: to limit unnecessary expert usage. To overcome this challenge, we introduce the budgeted deferral framework, which aims to train effective deferral algorithms while minimizing expert query costs during training. We propose new algorithms for both two-stage and single-stage multiple-expert deferral settings that selectively query only a subset of experts per training example. While inspired by active learning, our setting is fundamentally different: labels are already known, and the core challenge is to decide which experts to query in order to balance cost and predictive performance. We establish theoretical guarantees for both of our algorithms, including generalization bounds and label complexity analyses. Empirical results across several domains show that our algorithms substantially reduce training costs without sacrificing prediction accuracy, demonstrating the practical value of our budget-aware deferral algorithms.

Mastering Multiple-Expert Routing: Realizable $H$-Consistency and Strong Guarantees for Learning to Defer

The problem of learning to defer with multiple experts consists of optimally assigning input instances to experts, balancing the trade-off between their accuracy and computational cost. This is a critical challenge in natural language generation, but also in other fields such as image processing, and medical diagnostics. Recent studies have proposed surrogate loss functions to optimize deferral, but challenges remain in ensuring their consistency properties. This paper introduces novel surrogate loss functions and efficient algorithms with strong theoretical learning guarantees. We address open questions regarding realizable $H$-consistency, $H$-consistency bounds, and Bayes-consistency for both single-stage (jointly learning predictor and deferral function) and two-stage (learning only the deferral function with a fixed expert) learning scenarios. For single-stage deferral, we introduce a family of new realizable $H$-consistent surrogate losses and further prove $H$-consistency for a selected member. For two-stage deferral, we derive new surrogate losses that achieve realizable $H$-consistency, $H$-consistency bounds, and Bayes-consistency for the two-expert scenario and, under natural assumptions, multiple-expert scenario. Additionally, we provide enhanced theoretical guarantees under low-noise assumptions for both scenarios. Finally, we report the results of experiments using our proposed surrogate losses, comparing their performance against existing baselines.

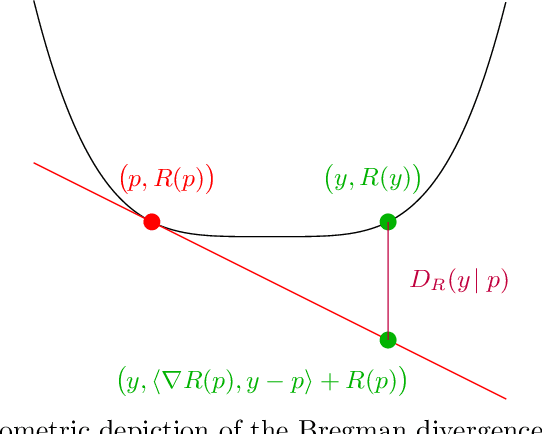
High-Dimensional Calibration from Swap Regret

We study the online calibration of multi-dimensional forecasts over an arbitrary convex set $\mathcal{P} \subset \mathbb{R}^d$ relative to an arbitrary norm $\Vert\cdot\Vert$. We connect this with the problem of external regret minimization for online linear optimization, showing that if it is possible to guarantee $O(\sqrt{\rho T})$ worst-case regret after $T$ rounds when actions are drawn from $\mathcal{P}$ and losses are drawn from the dual $\Vert \cdot \Vert_*$ unit norm ball, then it is also possible to obtain $\epsilon$-calibrated forecasts after $T = \exp(O(\rho /\epsilon^2))$ rounds. When $\mathcal{P}$ is the $d$-dimensional simplex and $\Vert \cdot \Vert$ is the $\ell_1$-norm, the existence of $O(\sqrt{T\log d})$-regret algorithms for learning with experts implies that it is possible to obtain $\epsilon$-calibrated forecasts after $T = \exp(O(\log{d}/\epsilon^2)) = d^{O(1/\epsilon^2)}$ rounds, recovering a recent result of Peng (2025). Interestingly, our algorithm obtains this guarantee without requiring access to any online linear optimization subroutine or knowledge of the optimal rate $\rho$ -- in fact, our algorithm is identical for every setting of $\mathcal{P}$ and $\Vert \cdot \Vert$. Instead, we show that the optimal regularizer for the above OLO problem can be used to upper bound the above calibration error by a swap regret, which we then minimize by running the recent TreeSwap algorithm with Follow-The-Leader as a subroutine. Finally, we prove that any online calibration algorithm that guarantees $\epsilon T$ $\ell_1$-calibration error over the $d$-dimensional simplex requires $T \geq \exp(\mathrm{poly}(1/\epsilon))$ (assuming $d \geq \mathrm{poly}(1/\epsilon)$). This strengthens the corresponding $d^{\Omega(\log{1/\epsilon})}$ lower bound of Peng, and shows that an exponential dependence on $1/\epsilon$ is necessary.