$H$-Consistency Guarantees for Regression
Paper and Code
Mar 28, 2024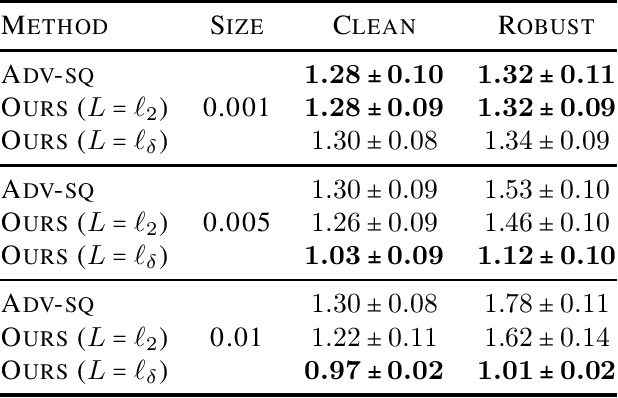
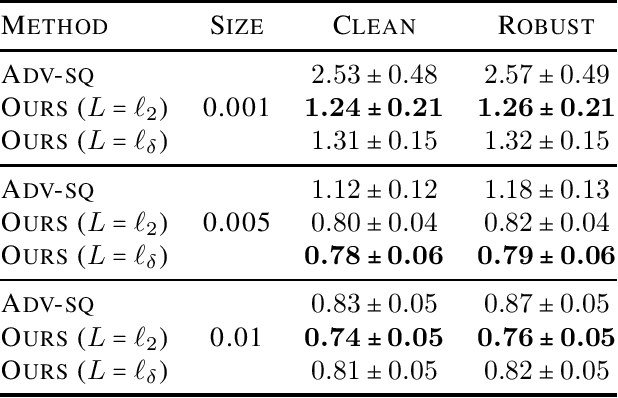
We present a detailed study of $H$-consistency bounds for regression. We first present new theorems that generalize the tools previously given to establish $H$-consistency bounds. This generalization proves essential for analyzing $H$-consistency bounds specific to regression. Next, we prove a series of novel $H$-consistency bounds for surrogate loss functions of the squared loss, under the assumption of a symmetric distribution and a bounded hypothesis set. This includes positive results for the Huber loss, all $\ell_p$ losses, $p \geq 1$, the squared $\epsilon$-insensitive loss, as well as a negative result for the $\epsilon$-insensitive loss used in squared Support Vector Regression (SVR). We further leverage our analysis of $H$-consistency for regression and derive principled surrogate losses for adversarial regression (Section 5). This readily establishes novel algorithms for adversarial regression, for which we report favorable experimental results in Section 6.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge