Cardinality-Aware Set Prediction and Top-$k$ Classification

We present a detailed study of cardinality-aware top-$k$ classification, a novel approach that aims to learn an accurate top-$k$ set predictor while maintaining a low cardinality. We introduce a new target loss function tailored to this setting that accounts for both the classification error and the cardinality of the set predicted. To optimize this loss function, we propose two families of surrogate losses: cost-sensitive comp-sum losses and cost-sensitive constrained losses. Minimizing these loss functions leads to new cardinality-aware algorithms that we describe in detail in the case of both top-$k$ and threshold-based classifiers. We establish $H$-consistency bounds for our cardinality-aware surrogate loss functions, thereby providing a strong theoretical foundation for our algorithms. We report the results of extensive experiments on CIFAR-10, CIFAR-100, ImageNet, and SVHN datasets demonstrating the effectiveness and benefits of our cardinality-aware algorithms.

Language Models with Conformal Factuality Guarantees

Guaranteeing the correctness and factuality of language model (LM) outputs is a major open problem. In this work, we propose conformal factuality, a framework that can ensure high probability correctness guarantees for LMs by connecting language modeling and conformal prediction. We observe that the correctness of an LM output is equivalent to an uncertainty quantification problem, where the uncertainty sets are defined as the entailment set of an LM's output. Using this connection, we show that conformal prediction in language models corresponds to a back-off algorithm that provides high probability correctness guarantees by progressively making LM outputs less specific (and expanding the associated uncertainty sets). This approach applies to any black-box LM and requires very few human-annotated samples. Evaluations of our approach on closed book QA (FActScore, NaturalQuestions) and reasoning tasks (MATH) show that our approach can provide 80-90% correctness guarantees while retaining the majority of the LM's original output.

Learning to Reject with a Fixed Predictor: Application to Decontextualization

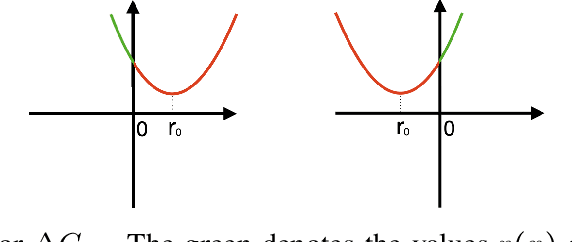
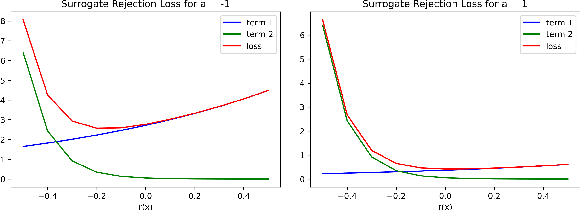
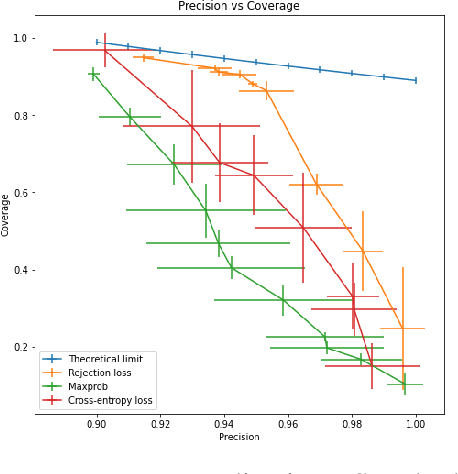
We study the problem of classification with a reject option for a fixed predictor, applicable in natural language processing. We introduce a new problem formulation for this scenario, and an algorithm minimizing a new surrogate loss function. We provide a complete theoretical analysis of the surrogate loss function with a strong $H$-consistency guarantee. For evaluation, we choose the decontextualization task, and provide a manually-labelled dataset of $2\mathord,000$ examples. Our algorithm significantly outperforms the baselines considered, with a $\sim\!\!25\%$ improvement in coverage when halving the error rate, which is only $\sim\!\! 3 \%$ away from the theoretical limit.

Online Learning Algorithms for Statistical Arbitrage

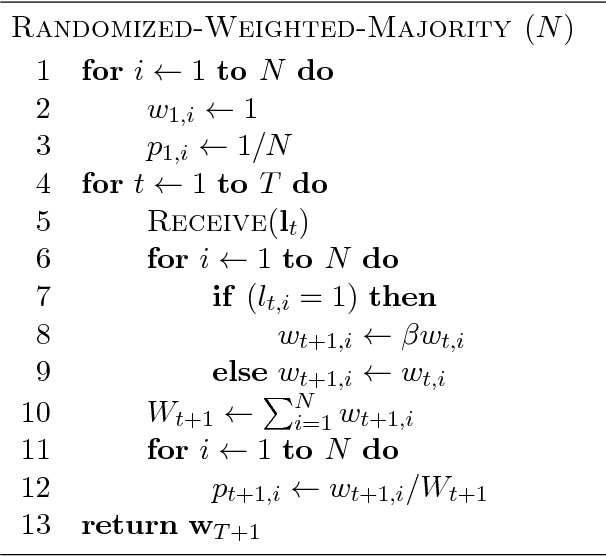
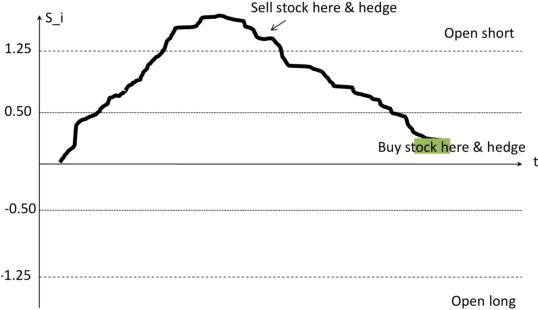
Statistical arbitrage is a class of financial trading strategies using mean reversion models. The corresponding techniques rely on a number of assumptions which may not hold for general non-stationary stochastic processes. This paper presents an alternative technique for statistical arbitrage based on online learning which does not require such assumptions and which benefits from strong learning guarantees.