Rate-Preserving Reductions for Blackwell Approachability

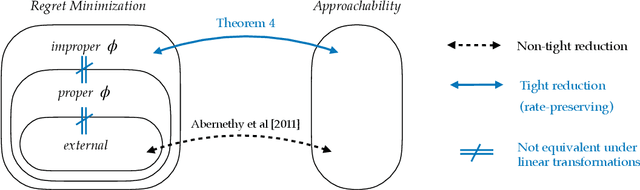
Abernethy et al. (2011) showed that Blackwell approachability and no-regret learning are equivalent, in the sense that any algorithm that solves a specific Blackwell approachability instance can be converted to a sublinear regret algorithm for a specific no-regret learning instance, and vice versa. In this paper, we study a more fine-grained form of such reductions, and ask when this translation between problems preserves not only a sublinear rate of convergence, but also preserves the optimal rate of convergence. That is, in which cases does it suffice to find the optimal regret bound for a no-regret learning instance in order to find the optimal rate of convergence for a corresponding approachability instance? We show that the reduction of Abernethy et al. (2011) does not preserve rates: their reduction may reduce a $d$-dimensional approachability instance $I_1$ with optimal convergence rate $R_1$ to a no-regret learning instance $I_2$ with optimal regret-per-round of $R_2$, with $R_{2}/R_{1}$ arbitrarily large (in particular, it is possible that $R_1 = 0$ and $R_{2} > 0$). On the other hand, we show that it is possible to tightly reduce any approachability instance to an instance of a generalized form of regret minimization we call improper $\phi$-regret minimization (a variant of the $\phi$-regret minimization of Gordon et al. (2008) where the transformation functions may map actions outside of the action set). Finally, we characterize when linear transformations suffice to reduce improper $\phi$-regret minimization problems to standard classes of regret minimization problems in a rate preserving manner. We prove that some improper $\phi$-regret minimization instances cannot be reduced to either subclass of instance in this way, suggesting that approachability can capture some problems that cannot be phrased in the language of online learning.

Strategically-Robust Learning Algorithms for Bidding in First-Price Auctions

Learning to bid in repeated first-price auctions is a fundamental problem at the interface of game theory and machine learning, which has seen a recent surge in interest due to the transition of display advertising to first-price auctions. In this work, we propose a novel concave formulation for pure-strategy bidding in first-price auctions, and use it to analyze natural Gradient-Ascent-based algorithms for this problem. Importantly, our analysis goes beyond regret, which was the typical focus of past work, and also accounts for the strategic backdrop of online-advertising markets where bidding algorithms are deployed -- we prove that our algorithms cannot be exploited by a strategic seller and that they incentivize truth-telling for the buyer. Concretely, we show that our algorithms achieve $O(\sqrt{T})$ regret when the highest competing bids are generated adversarially, and show that no online algorithm can do better. We further prove that the regret improves to $O(\log T)$ when the competition is stationary and stochastic. Moving beyond regret, we show that a strategic seller cannot exploit our algorithms to extract more revenue on average than is possible under the optimal mechanism, i.e., the seller cannot do much better than posting the monopoly reserve price in each auction. Finally, we prove that our algorithm is also incentive compatible -- it is a (nearly) dominant strategy for the buyer to report her values truthfully to the algorithm as a whole.

Pseudonorm Approachability and Applications to Regret Minimization

Blackwell's celebrated approachability theory provides a general framework for a variety of learning problems, including regret minimization. However, Blackwell's proof and implicit algorithm measure approachability using the $\ell_2$ (Euclidean) distance. We argue that in many applications such as regret minimization, it is more useful to study approachability under other distance metrics, most commonly the $\ell_\infty$-metric. But, the time and space complexity of the algorithms designed for $\ell_\infty$-approachability depend on the dimension of the space of the vectorial payoffs, which is often prohibitively large. Thus, we present a framework for converting high-dimensional $\ell_\infty$-approachability problems to low-dimensional pseudonorm approachability problems, thereby resolving such issues. We first show that the $\ell_\infty$-distance between the average payoff and the approachability set can be equivalently defined as a pseudodistance between a lower-dimensional average vector payoff and a new convex set we define. Next, we develop an algorithmic theory of pseudonorm approachability, analogous to previous work on approachability for $\ell_2$ and other norms, showing that it can be achieved via online linear optimization (OLO) over a convex set given by the Fenchel dual of the unit pseudonorm ball. We then use that to show, modulo mild normalization assumptions, that there exists an $\ell_\infty$-approachability algorithm whose convergence is independent of the dimension of the original vectorial payoff. We further show that that algorithm admits a polynomial-time complexity, assuming that the original $\ell_\infty$-distance can be computed efficiently. We also give an $\ell_\infty$-approachability algorithm whose convergence is logarithmic in that dimension using an FTRL algorithm with a maximum-entropy regularizer.

Robust Budget Pacing with a Single Sample

Major Internet advertising platforms offer budget pacing tools as a standard service for advertisers to manage their ad campaigns. Given the inherent non-stationarity in an advertiser's value and also competing advertisers' values over time, a commonly used approach is to learn a target expenditure plan that specifies a target spend as a function of time, and then run a controller that tracks this plan. This raises the question: how many historical samples are required to learn a good expenditure plan? We study this question by considering an advertiser repeatedly participating in $T$ second-price auctions, where the tuple of her value and the highest competing bid is drawn from an unknown time-varying distribution. The advertiser seeks to maximize her total utility subject to her budget constraint. Prior work has shown the sufficiency of $T\log T$ samples per distribution to achieve the optimal $O(\sqrt{T})$-regret. We dramatically improve this state-of-the-art and show that just one sample per distribution is enough to achieve the near-optimal $\tilde O(\sqrt{T})$-regret, while still being robust to noise in the sampling distributions.

Strategizing against Learners in Bayesian Games

We study repeated two-player games where one of the players, the learner, employs a no-regret learning strategy, while the other, the optimizer, is a rational utility maximizer. We consider general Bayesian games, where the payoffs of both the optimizer and the learner could depend on the type, which is drawn from a publicly known distribution, but revealed privately to the learner. We address the following questions: (a) what is the bare minimum that the optimizer can guarantee to obtain regardless of the no-regret learning algorithm employed by the learner? (b) are there learning algorithms that cap the optimizer payoff at this minimum? (c) can these algorithms be implemented efficiently? While building this theory of optimizer-learner interactions, we define a new combinatorial notion of regret called polytope swap regret, that could be of independent interest in other settings.

From Online Optimization to PID Controllers: Mirror Descent with Momentum

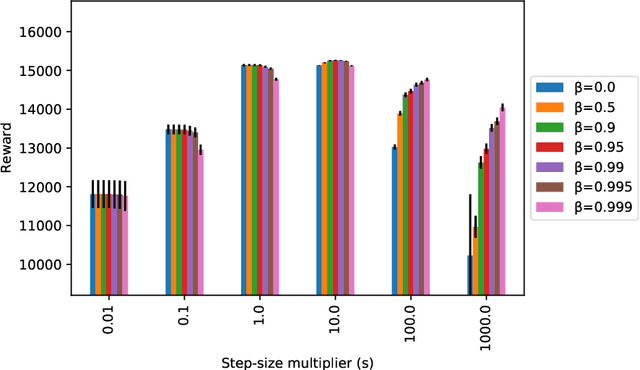
We study a family of first-order methods with momentum based on mirror descent for online convex optimization, which we dub online mirror descent with momentum (OMDM). Our algorithms include as special cases gradient descent and exponential weights update with momentum. We provide a new and simple analysis of momentum-based methods in a stochastic setting that yields a regret bound that decreases as momentum increases. This immediately establishes that momentum can help in the convergence of stochastic subgradient descent in convex nonsmooth optimization. We showcase the robustness of our algorithm by also providing an analysis in an adversarial setting that gives the first non-trivial regret bounds for OMDM. Our work aims to provide a better understanding of the benefits of momentum-based methods, which despite their recent empirical success, is incomplete. Finally, we discuss how OMDM can be applied to stochastic online allocation problems, which are central problems in computer science and operations research. In doing so, we establish an important connection between OMDM and popular approaches from optimal control such as PID controllers, thereby providing regret bounds on the performance of PID controllers. The improvements of momentum are most pronounced when the step-size is large, thereby indicating that momentum provides a robustness to misspecification of tuning parameters. We provide a numerical evaluation that verifies the robustness of our algorithms.

Learning to Price Against a Moving Target

In the Learning to Price setting, a seller posts prices over time with the goal of maximizing revenue while learning the buyer's valuation. This problem is very well understood when values are stationary (fixed or iid). Here we study the problem where the buyer's value is a moving target, i.e., they change over time either by a stochastic process or adversarially with bounded variation. In either case, we provide matching upper and lower bounds on the optimal revenue loss. Since the target is moving, any information learned soon becomes out-dated, which forces the algorithms to keep switching between exploring and exploiting phases.

Tight Lower Bounds for Multiplicative Weights Algorithmic Families

We study the fundamental problem of prediction with expert advice and develop regret lower bounds for a large family of algorithms for this problem. We develop simple adversarial primitives, that lend themselves to various combinations leading to sharp lower bounds for many algorithmic families. We use these primitives to show that the classic Multiplicative Weights Algorithm (MWA) has a regret of $\sqrt{\frac{T \ln k}{2}}$, there by completely closing the gap between upper and lower bounds. We further show a regret lower bound of $\frac{2}{3}\sqrt{\frac{T\ln k}{2}}$ for a much more general family of algorithms than MWA, where the learning rate can be arbitrarily varied over time, or even picked from arbitrary distributions over time. We also use our primitives to construct adversaries in the geometric horizon setting for MWA to precisely characterize the regret at $\frac{0.391}{\sqrt{\delta}}$ for the case of $2$ experts and a lower bound of $\frac{1}{2}\sqrt{\frac{\ln k}{2\delta}}$ for the case of arbitrary number of experts $k$.

Towards Optimal Algorithms for Prediction with Expert Advice

We study the classical problem of prediction with expert advice in the adversarial setting with a geometric stopping time. In 1965, Cover gave the optimal algorithm for the case of 2 experts. In this paper, we design the optimal algorithm, adversary and regret for the case of 3 experts. Further, we show that the optimal algorithm for $2$ and $3$ experts is a probability matching algorithm (analogous to Thompson sampling) against a particular randomized adversary. Remarkably, our proof shows that the probability matching algorithm is not only optimal against this particular randomized adversary, but also minimax optimal. Our analysis develops upper and lower bounds simultaneously, analogous to the primal-dual method. Our analysis of the optimal adversary goes through delicate asymptotics of the random walk of a particle between multiple walls. We use the connection we develop to random walks to derive an improved algorithm and regret bound for the case of $4$ experts, and, provide a general framework for designing the optimal algorithm and adversary for an arbitrary number of experts.