Allocating Variance to Maximize Expectation

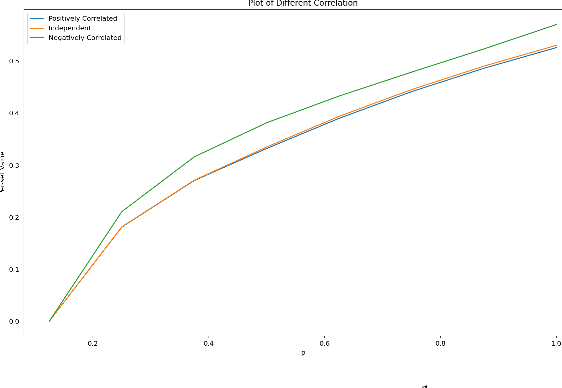
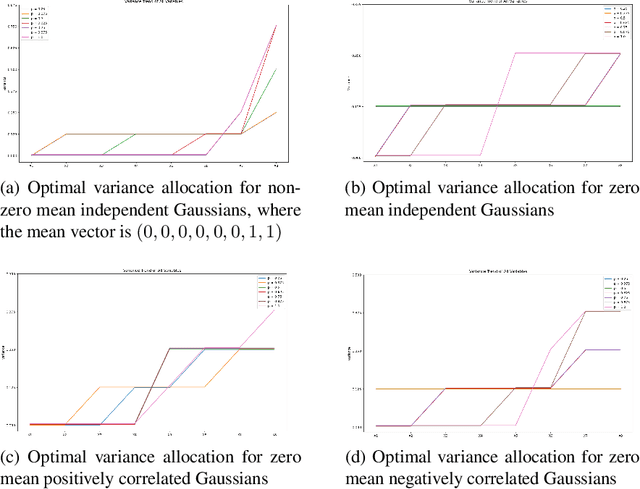
We design efficient approximation algorithms for maximizing the expectation of the supremum of families of Gaussian random variables. In particular, let $\mathrm{OPT}:=\max_{\sigma_1,\cdots,\sigma_n}\mathbb{E}\left[\sum_{j=1}^{m}\max_{i\in S_j} X_i\right]$, where $X_i$ are Gaussian, $S_j\subset[n]$ and $\sum_i\sigma_i^2=1$, then our theoretical results include: - We characterize the optimal variance allocation -- it concentrates on a small subset of variables as $|S_j|$ increases, - A polynomial time approximation scheme (PTAS) for computing $\mathrm{OPT}$ when $m=1$, and - An $O(\log n)$ approximation algorithm for computing $\mathrm{OPT}$ for general $m>1$. Such expectation maximization problems occur in diverse applications, ranging from utility maximization in auctions markets to learning mixture models in quantitative genetics.

Full Swap Regret and Discretized Calibration

We study the problem of minimizing swap regret in structured normal-form games. Players have a very large (potentially infinite) number of pure actions, but each action has an embedding into $d$-dimensional space and payoffs are given by bilinear functions of these embeddings. We provide an efficient learning algorithm for this setting that incurs at most $\tilde{O}(T^{(d+1)/(d+3)})$ swap regret after $T$ rounds. To achieve this, we introduce a new online learning problem we call \emph{full swap regret minimization}. In this problem, a learner repeatedly takes a (randomized) action in a bounded convex $d$-dimensional action set $\mathcal{K}$ and then receives a loss from the adversary, with the goal of minimizing their regret with respect to the \emph{worst-case} swap function mapping $\mathcal{K}$ to $\mathcal{K}$. For varied assumptions about the convexity and smoothness of the loss functions, we design algorithms with full swap regret bounds ranging from $O(T^{d/(d+2)})$ to $O(T^{(d+1)/(d+2)})$. Finally, we apply these tools to the problem of online forecasting to minimize calibration error, showing that several notions of calibration can be viewed as specific instances of full swap regret. In particular, we design efficient algorithms for online forecasting that guarantee at most $O(T^{1/3})$ $\ell_2$-calibration error and $O(\max(\sqrt{\epsilon T}, T^{1/3}))$ \emph{discretized-calibration} error (when the forecaster is restricted to predicting multiples of $\epsilon$).

Learning Thresholds with Latent Values and Censored Feedback

In this paper, we investigate a problem of actively learning threshold in latent space, where the unknown reward $g(\gamma, v)$ depends on the proposed threshold $\gamma$ and latent value $v$ and it can be $only$ achieved if the threshold is lower than or equal to the unknown latent value. This problem has broad applications in practical scenarios, e.g., reserve price optimization in online auctions, online task assignments in crowdsourcing, setting recruiting bars in hiring, etc. We first characterize the query complexity of learning a threshold with the expected reward at most $\epsilon$ smaller than the optimum and prove that the number of queries needed can be infinitely large even when $g(\gamma, v)$ is monotone with respect to both $\gamma$ and $v$. On the positive side, we provide a tight query complexity $\tilde{\Theta}(1/\epsilon^3)$ when $g$ is monotone and the CDF of value distribution is Lipschitz. Moreover, we show a tight $\tilde{\Theta}(1/\epsilon^3)$ query complexity can be achieved as long as $g$ satisfies one-sided Lipschitzness, which provides a complete characterization for this problem. Finally, we extend this model to an online learning setting and demonstrate a tight $\Theta(T^{2/3})$ regret bound using continuous-arm bandit techniques and the aforementioned query complexity results.

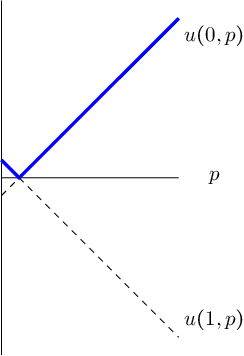
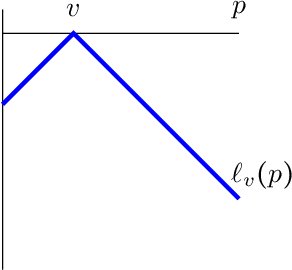
U-Calibration: Forecasting for an Unknown Agent

We consider the problem of evaluating forecasts of binary events whose predictions are consumed by rational agents who take an action in response to a prediction, but whose utility is unknown to the forecaster. We show that optimizing forecasts for a single scoring rule (e.g., the Brier score) cannot guarantee low regret for all possible agents. In contrast, forecasts that are well-calibrated guarantee that all agents incur sublinear regret. However, calibration is not a necessary criterion here (it is possible for miscalibrated forecasts to provide good regret guarantees for all possible agents), and calibrated forecasting procedures have provably worse convergence rates than forecasting procedures targeting a single scoring rule. Motivated by this, we present a new metric for evaluating forecasts that we call U-calibration, equal to the maximal regret of the sequence of forecasts when evaluated under any bounded scoring rule. We show that sublinear U-calibration error is a necessary and sufficient condition for all agents to achieve sublinear regret guarantees. We additionally demonstrate how to compute the U-calibration error efficiently and provide an online algorithm that achieves $O(\sqrt{T})$ U-calibration error (on par with optimal rates for optimizing for a single scoring rule, and bypassing lower bounds for the traditionally calibrated learning procedures). Finally, we discuss generalizations to the multiclass prediction setting.

Learning to Price Against a Moving Target

In the Learning to Price setting, a seller posts prices over time with the goal of maximizing revenue while learning the buyer's valuation. This problem is very well understood when values are stationary (fixed or iid). Here we study the problem where the buyer's value is a moving target, i.e., they change over time either by a stochastic process or adversarially with bounded variation. In either case, we provide matching upper and lower bounds on the optimal revenue loss. Since the target is moving, any information learned soon becomes out-dated, which forces the algorithms to keep switching between exploring and exploiting phases.