IDA-Bench: Evaluating LLMs on Interactive Guided Data Analysis

Large Language Models (LLMs) show promise as data analysis agents, but existing benchmarks overlook the iterative nature of the field, where experts' decisions evolve with deeper insights of the dataset. To address this, we introduce IDA-Bench, a novel benchmark evaluating LLM agents in multi-round interactive scenarios. Derived from complex Kaggle notebooks, tasks are presented as sequential natural language instructions by an LLM-simulated user. Agent performance is judged by comparing its final numerical output to the human-derived baseline. Initial results show that even state-of-the-art coding agents (like Claude-3.7-thinking) succeed on < 50% of the tasks, highlighting limitations not evident in single-turn tests. This work underscores the need to improve LLMs' multi-round capabilities for building more reliable data analysis agents, highlighting the necessity of achieving a balance between instruction following and reasoning.

TinyAlign: Boosting Lightweight Vision-Language Models by Mitigating Modal Alignment Bottlenecks

Lightweight Vision-Language Models (VLMs) are indispensable for resource-constrained applications. The prevailing approach to aligning vision and language models involves freezing both the vision encoder and the language model while training small connector modules. However, this strategy heavily depends on the intrinsic capabilities of the language model, which can be suboptimal for lightweight models with limited representational capacity. In this work, we investigate this alignment bottleneck through the lens of mutual information, demonstrating that the constrained capacity of the language model inherently limits the Effective Mutual Information (EMI) between multimodal inputs and outputs, thereby compromising alignment quality. To address this challenge, we propose TinyAlign, a novel framework inspired by Retrieval-Augmented Generation, which strategically retrieves relevant context from a memory bank to enrich multimodal inputs and enhance their alignment. Extensive empirical evaluations reveal that TinyAlign significantly reduces training loss, accelerates convergence, and enhances task performance. Remarkably, it allows models to achieve baseline-level performance with only 40\% of the fine-tuning data, highlighting exceptional data efficiency. Our work thus offers a practical pathway for developing more capable lightweight VLMs while introducing a fresh theoretical lens to better understand and address alignment bottlenecks in constrained multimodal systems.

Implementing Long Text Style Transfer with LLMs through Dual-Layered Sentence and Paragraph Structure Extraction and Mapping

This paper addresses the challenge in long-text style transfer using zero-shot learning of large language models (LLMs), proposing a hierarchical framework that combines sentence-level stylistic adaptation with paragraph-level structural coherence. We argue that in the process of effective paragraph-style transfer, to preserve the consistency of original syntactic and semantic information, it is essential to perform style transfer not only at the sentence level but also to incorporate paragraph-level semantic considerations, while ensuring structural coherence across inter-sentential relationships. Our proposed framework, ZeroStylus, operates through two systematic phases: hierarchical template acquisition from reference texts and template-guided generation with multi-granular matching. The framework dynamically constructs sentence and paragraph template repositories, enabling context-aware transformations while preserving inter-sentence logical relationships. Experimental evaluations demonstrate significant improvements over baseline methods, with structured rewriting achieving 6.90 average score compared to 6.70 for direct prompting approaches in tri-axial metrics assessing style consistency, content preservation, and expression quality. Ablation studies validate the necessity of both template hierarchies during style transfer, showing higher content preservation win rate against sentence-only approaches through paragraph-level structural encoding, as well as direct prompting method through sentence-level pattern extraction and matching. The results establish new capabilities for coherent long-text style transfer without requiring parallel corpora or LLM fine-tuning.

Survey on Strategic Mining in Blockchain: A Reinforcement Learning Approach

Strategic mining attacks, such as selfish mining, exploit blockchain consensus protocols by deviating from honest behavior to maximize rewards. Markov Decision Process (MDP) analysis faces scalability challenges in modern digital economics, including blockchain. To address these limitations, reinforcement learning (RL) provides a scalable alternative, enabling adaptive strategy optimization in complex dynamic environments. In this survey, we examine RL's role in strategic mining analysis, comparing it to MDP-based approaches. We begin by reviewing foundational MDP models and their limitations, before exploring RL frameworks that can learn near-optimal strategies across various protocols. Building on this analysis, we compare RL techniques and their effectiveness in deriving security thresholds, such as the minimum attacker power required for profitable attacks. Expanding the discussion further, we classify consensus protocols and propose open challenges, such as multi-agent dynamics and real-world validation. This survey highlights the potential of reinforcement learning (RL) to address the challenges of selfish mining, including protocol design, threat detection, and security analysis, while offering a strategic roadmap for researchers in decentralized systems and AI-driven analytics.

Large-Scale Contextual Market Equilibrium Computation through Deep Learning

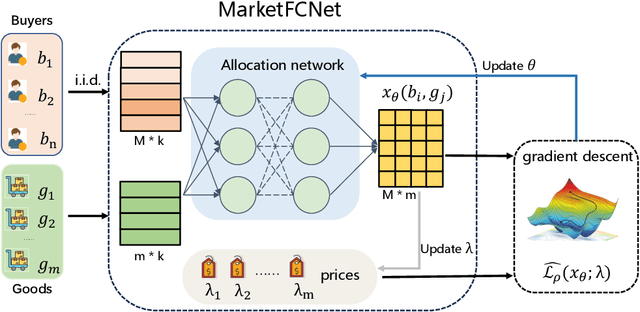
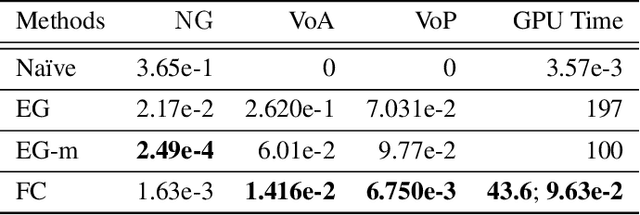
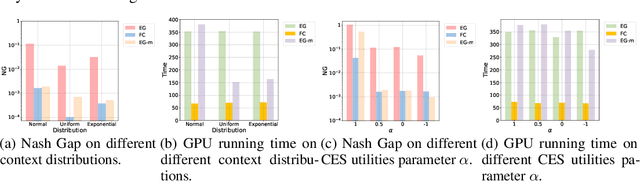
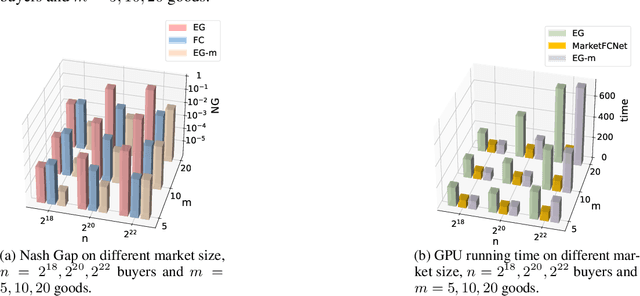
Market equilibrium is one of the most fundamental solution concepts in economics and social optimization analysis. Existing works on market equilibrium computation primarily focus on settings with a relatively small number of buyers. Motivated by this, our paper investigates the computation of market equilibrium in scenarios with a large-scale buyer population, where buyers and goods are represented by their contexts. Building on this realistic and generalized contextual market model, we introduce MarketFCNet, a deep learning-based method for approximating market equilibrium. We start by parameterizing the allocation of each good to each buyer using a neural network, which depends solely on the context of the buyer and the good. Next, we propose an efficient method to estimate the loss function of the training algorithm unbiasedly, enabling us to optimize the network parameters through gradient descent. To evaluate the approximated solution, we introduce a metric called Nash Gap, which quantifies the deviation of the given allocation and price pair from the market equilibrium. Experimental results indicate that MarketFCNet delivers competitive performance and significantly lower running times compared to existing methods as the market scale expands, demonstrating the potential of deep learning-based methods to accelerate the approximation of large-scale contextual market equilibrium.

Hummer: Towards Limited Competitive Preference Dataset

Preference datasets are essential for incorporating human preferences into pre-trained language models, playing a key role in the success of Reinforcement Learning from Human Feedback. However, these datasets often demonstrate conflicting alignment objectives, leading to increased vulnerability to jailbreak attacks and challenges in adapting downstream tasks to prioritize specific alignment objectives without negatively impacting others. In this work, we introduce a novel statistical metric, Alignment Dimension Conflict, to quantify the degree of conflict within preference datasets. We then present \texttt{Hummer} and its fine-grained variant, \texttt{Hummer-F}, as innovative pairwise preference datasets with reduced-conflict alignment objectives. \texttt{Hummer} is built based on UltraFeedback and is enhanced by AI feedback from GPT-4, marking as the first preference dataset aimed at reducing the competition between alignment objectives. Furthermore, we develop reward models, HummerRM and HummerRM-F, which employ a hybrid sampling approach to balance diverse alignment objectives effectively. This sampling method positions HummerRM as an ideal model for domain-specific further fine-tuning and reducing vulnerabilities to attacks.

Are Bounded Contracts Learnable and Approximately Optimal?

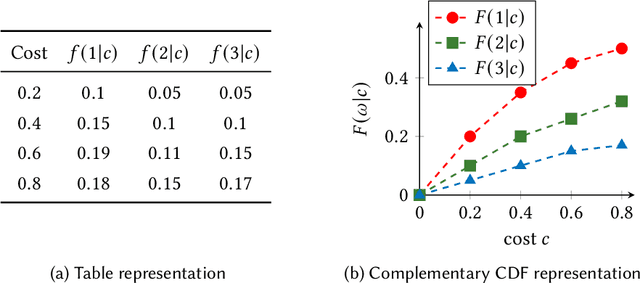
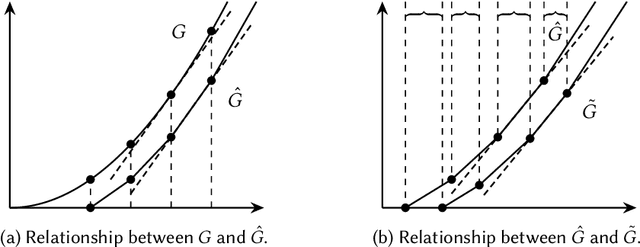
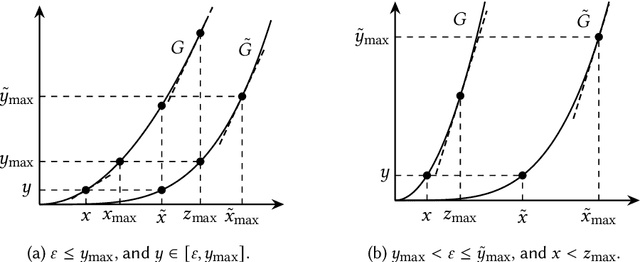
This paper considers the hidden-action model of the principal-agent problem, in which a principal incentivizes an agent to work on a project using a contract. We investigate whether contracts with bounded payments are learnable and approximately optimal. Our main results are two learning algorithms that can find a nearly optimal bounded contract using a polynomial number of queries, under two standard assumptions in the literature: a costlier action for the agent leads to a better outcome distribution for the principal, and the agent's cost/effort has diminishing returns. Our polynomial query complexity upper bound shows that standard assumptions are sufficient for achieving an exponential improvement upon the known lower bound for general instances. Unlike the existing algorithms, which relied on discretizing the contract space, our algorithms directly learn the underlying outcome distributions. As for the approximate optimality of bounded contracts, we find that they could be far from optimal in terms of multiplicative or additive approximation, but satisfy a notion of mixed approximation.

Scalable Virtual Valuations Combinatorial Auction Design by Combining Zeroth-Order and First-Order Optimization Method

Automated auction design seeks to discover empirically high-revenue and incentive-compatible mechanisms using machine learning. Ensuring dominant strategy incentive compatibility (DSIC) is crucial, and the most effective approach is to confine the mechanism to Affine Maximizer Auctions (AMAs). Nevertheless, existing AMA-based approaches encounter challenges such as scalability issues (arising from combinatorial candidate allocations) and the non-differentiability of revenue. In this paper, to achieve a scalable AMA-based method, we further restrict the auction mechanism to Virtual Valuations Combinatorial Auctions (VVCAs), a subset of AMAs with significantly fewer parameters. Initially, we employ a parallelizable dynamic programming algorithm to compute the winning allocation of a VVCA. Subsequently, we propose a novel optimization method that combines both zeroth-order and first-order techniques to optimize the VVCA parameters. Extensive experiments demonstrate the efficacy and scalability of our proposed approach, termed Zeroth-order and First-order Optimization of VVCAs (ZFO-VVCA), particularly when applied to large-scale auctions.

A survey on algorithms for Nash equilibria in finite normal-form games

Nash equilibrium is one of the most influential solution concepts in game theory. With the development of computer science and artificial intelligence, there is an increasing demand on Nash equilibrium computation, especially for Internet economics and multi-agent learning. This paper reviews various algorithms computing the Nash equilibrium and its approximation solutions in finite normal-form games from both theoretical and empirical perspectives. For the theoretical part, we classify algorithms in the literature and present basic ideas on algorithm design and analysis. For the empirical part, we present a comprehensive comparison on the algorithms in the literature over different kinds of games. Based on these results, we provide practical suggestions on implementations and uses of these algorithms. Finally, we present a series of open problems from both theoretical and practical considerations.

Learning Thresholds with Latent Values and Censored Feedback

In this paper, we investigate a problem of actively learning threshold in latent space, where the unknown reward $g(\gamma, v)$ depends on the proposed threshold $\gamma$ and latent value $v$ and it can be $only$ achieved if the threshold is lower than or equal to the unknown latent value. This problem has broad applications in practical scenarios, e.g., reserve price optimization in online auctions, online task assignments in crowdsourcing, setting recruiting bars in hiring, etc. We first characterize the query complexity of learning a threshold with the expected reward at most $\epsilon$ smaller than the optimum and prove that the number of queries needed can be infinitely large even when $g(\gamma, v)$ is monotone with respect to both $\gamma$ and $v$. On the positive side, we provide a tight query complexity $\tilde{\Theta}(1/\epsilon^3)$ when $g$ is monotone and the CDF of value distribution is Lipschitz. Moreover, we show a tight $\tilde{\Theta}(1/\epsilon^3)$ query complexity can be achieved as long as $g$ satisfies one-sided Lipschitzness, which provides a complete characterization for this problem. Finally, we extend this model to an online learning setting and demonstrate a tight $\Theta(T^{2/3})$ regret bound using continuous-arm bandit techniques and the aforementioned query complexity results.