Get our free extension to see links to code for papers anywhere online!

Chrome logo  Add to Chrome

Firefox logo Add to Firefox
Picture for David Henry Mguni

David Henry Mguni
Alert button

Learning Risk-Averse Equilibria in Multi-Agent Systems


May 30, 2022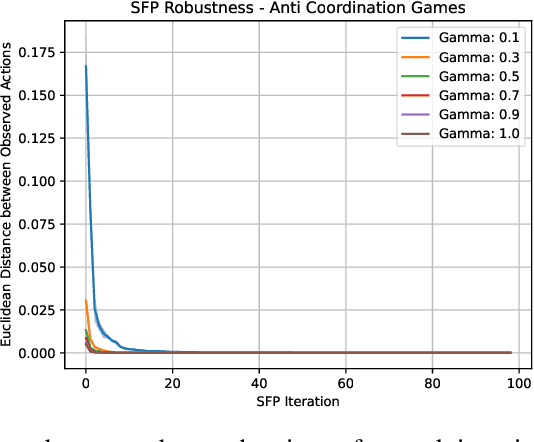
Oliver Slumbers, David Henry Mguni, Stephen McAleer, Jun Wang, Yaodong Yang

Add code
Alert button

Figure 1 for Learning Risk-Averse Equilibria in Multi-Agent Systems
Figure 2 for Learning Risk-Averse Equilibria in Multi-Agent Systems
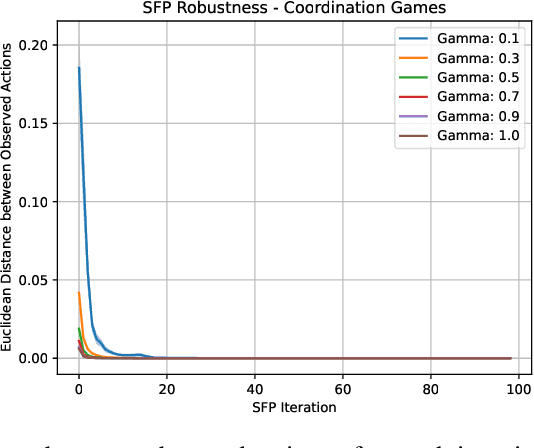
Figure 3 for Learning Risk-Averse Equilibria in Multi-Agent Systems
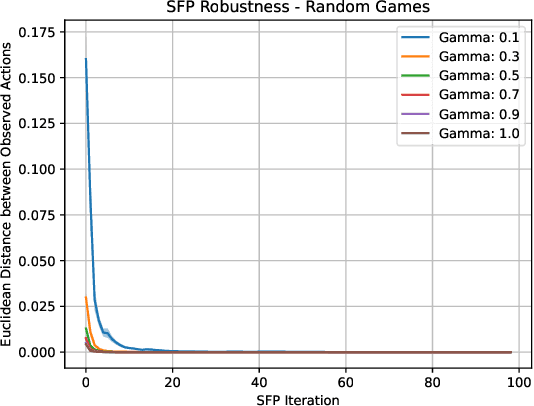
Figure 4 for Learning Risk-Averse Equilibria in Multi-Agent Systems

   Access Paper or Ask Questions
  • Share via Twitter
  • Share via Facebook
  • Share via LinkedIn
  • Share via Whatsapp
  • Share via Messenger
  • Share via Email

Online Markov Decision Processes with Non-oblivious Strategic Adversary


Oct 08, 2021
Le Cong Dinh, David Henry Mguni, Long Tran-Thanh, Jun Wang, Yaodong Yang

Add code
Alert button

Figure 1 for Online Markov Decision Processes with Non-oblivious Strategic Adversary

   Access Paper or Ask Questions
  • Share via Twitter
  • Share via Facebook
  • Share via LinkedIn
  • Share via Whatsapp
  • Share via Messenger
  • Share via Email

On the Complexity of Computing Markov Perfect Equilibrium in General-Sum Stochastic Games


Sep 04, 2021
Xiaotie Deng, Yuhao Li, David Henry Mguni, Jun Wang, Yaodong Yang

Add code
Alert button


   Access Paper or Ask Questions
  • Share via Twitter
  • Share via Facebook
  • Share via LinkedIn
  • Share via Whatsapp
  • Share via Messenger
  • Share via Email

Settling the Variance of Multi-Agent Policy Gradients


Aug 20, 2021
Jakub Grudzien Kuba, Muning Wen, Yaodong Yang, Linghui Meng, Shangding Gu, Haifeng Zhang, David Henry Mguni, Jun Wang

Add code
Alert button

Figure 1 for Settling the Variance of Multi-Agent Policy Gradients
Figure 2 for Settling the Variance of Multi-Agent Policy Gradients
Figure 3 for Settling the Variance of Multi-Agent Policy Gradients

   Access Paper or Ask Questions
  • Share via Twitter
  • Share via Facebook
  • Share via LinkedIn
  • Share via Whatsapp
  • Share via Messenger
  • Share via Email

Online Double Oracle


Mar 16, 2021
Le Cong Dinh, Yaodong Yang, Zheng Tian, Nicolas Perez Nieves, Oliver Slumbers, David Henry Mguni, Haitham Bou Ammar, Jun Wang

Add code
Alert button

Figure 1 for Online Double Oracle
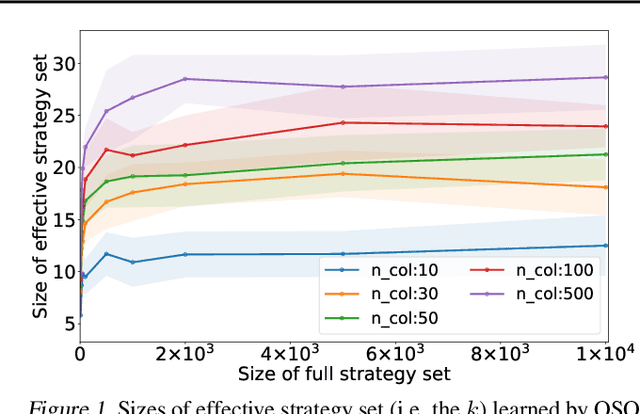
Figure 2 for Online Double Oracle
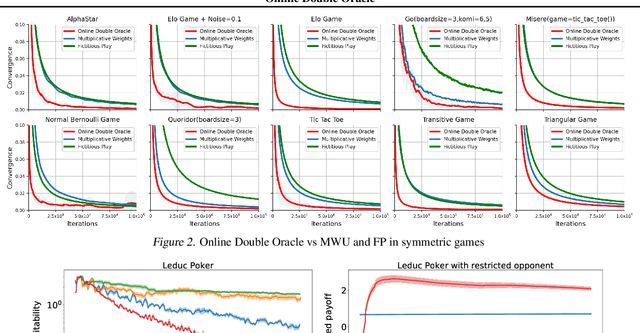
Figure 3 for Online Double Oracle
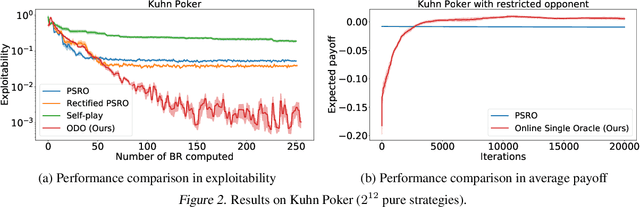
Figure 4 for Online Double Oracle
* [email protected] 
   Access Paper or Ask Questions
  • Share via Twitter
  • Share via Facebook
  • Share via LinkedIn
  • Share via Whatsapp
  • Share via Messenger
  • Share via Email

Modelling Behavioural Diversity for Learning in Open-Ended Games


Mar 14, 2021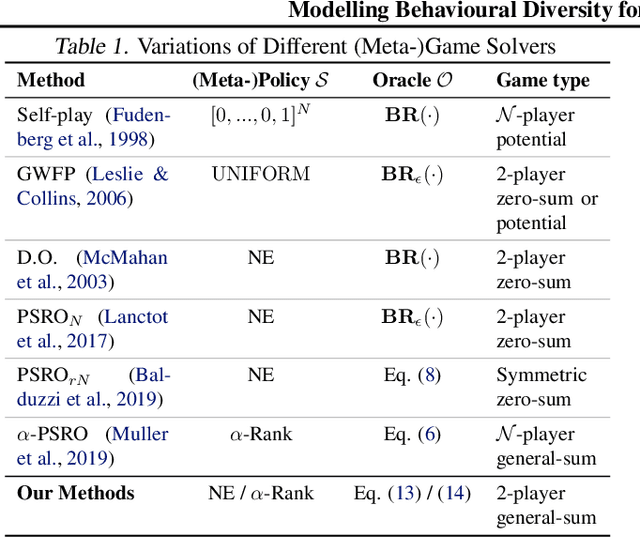
Nicolas Perez Nieves, Yaodong Yang, Oliver Slumbers, David Henry Mguni, Jun Wang

Add code
Alert button

Figure 1 for Modelling Behavioural Diversity for Learning in Open-Ended Games
Figure 2 for Modelling Behavioural Diversity for Learning in Open-Ended Games
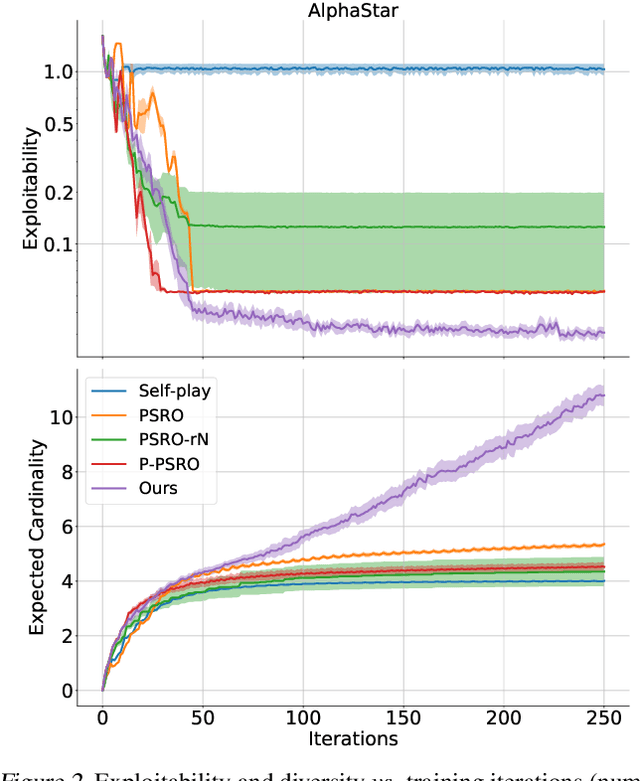
Figure 3 for Modelling Behavioural Diversity for Learning in Open-Ended Games
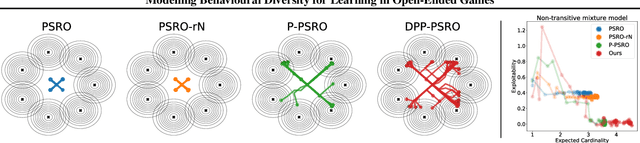
Figure 4 for Modelling Behavioural Diversity for Learning in Open-Ended Games
* corresponds to  
   Access Paper or Ask Questions
  • Share via Twitter
  • Share via Facebook
  • Share via LinkedIn
  • Share via Whatsapp
  • Share via Messenger
  • Share via Email