Online Double Oracle
Paper and Code
Mar 16, 2021
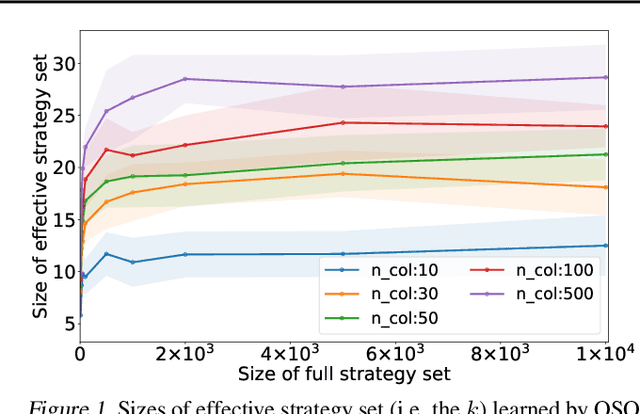
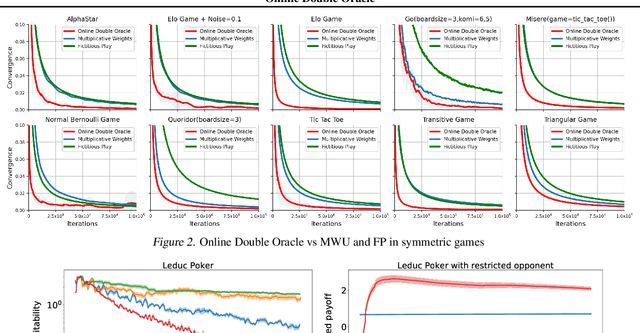
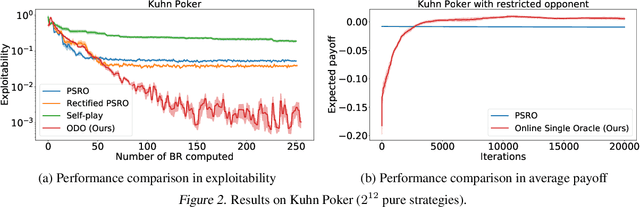
Solving strategic games whose action space is prohibitively large is a critical yet under-explored topic in economics, computer science and artificial intelligence. This paper proposes new learning algorithms in two-player zero-sum games where the number of pure strategies is huge or even infinite. Specifically, we combine no-regret analysis from online learning with double oracle methods from game theory. Our method -- \emph{Online Double Oracle (ODO)} -- achieves the regret bound of $\mathcal{O}(\sqrt{T k \log(k)})$ in self-play setting where $k$ is NOT the size of the game, but rather the size of \emph{effective strategy set} that is linearly dependent on the support size of the Nash equilibrium. On tens of different real-world games, including Leduc Poker that contains $3^{936}$ pure strategies, our methods outperform no-regret algorithms and double oracle methods by a large margin, both in convergence rate to Nash equilibrium and average payoff against strategic adversary.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge