Achieving Better Regret against Strategic Adversaries

We study online learning problems in which the learner has extra knowledge about the adversary's behaviour, i.e., in game-theoretic settings where opponents typically follow some no-external regret learning algorithms. Under this assumption, we propose two new online learning algorithms, Accurate Follow the Regularized Leader (AFTRL) and Prod-Best Response (Prod-BR), that intensively exploit this extra knowledge while maintaining the no-regret property in the worst-case scenario of having inaccurate extra information. Specifically, AFTRL achieves $O(1)$ external regret or $O(1)$ \emph{forward regret} against no-external regret adversary in comparison with $O(\sqrt{T})$ \emph{dynamic regret} of Prod-BR. To the best of our knowledge, our algorithm is the first to consider forward regret that achieves $O(1)$ regret against strategic adversaries. When playing zero-sum games with Accurate Multiplicative Weights Update (AMWU), a special case of AFTRL, we achieve \emph{last round convergence} to the Nash Equilibrium. We also provide numerical experiments to further support our theoretical results. In particular, we demonstrate that our methods achieve significantly better regret bounds and rate of last round convergence, compared to the state of the art (e.g., Multiplicative Weights Update (MWU) and its optimistic counterpart, OMWU).

Online Markov Decision Processes with Non-oblivious Strategic Adversary

We study a novel setting in Online Markov Decision Processes (OMDPs) where the loss function is chosen by a non-oblivious strategic adversary who follows a no-external regret algorithm. In this setting, we first demonstrate that MDP-Expert, an existing algorithm that works well with oblivious adversaries can still apply and achieve a policy regret bound of $\mathcal{O}(\sqrt{T \log(L)}+\tau^2\sqrt{ T \log(|A|)})$ where $L$ is the size of adversary's pure strategy set and $|A|$ denotes the size of agent's action space. Considering real-world games where the support size of a NE is small, we further propose a new algorithm: MDP-Online Oracle Expert (MDP-OOE), that achieves a policy regret bound of $\mathcal{O}(\sqrt{T\log(L)}+\tau^2\sqrt{ T k \log(k)})$ where $k$ depends only on the support size of the NE. MDP-OOE leverages the key benefit of Double Oracle in game theory and thus can solve games with prohibitively large action space. Finally, to better understand the learning dynamics of no-regret methods, under the same setting of no-external regret adversary in OMDPs, we introduce an algorithm that achieves last-round convergence result to a NE. To our best knowledge, this is first work leading to the last iteration result in OMDPs.

Online Double Oracle

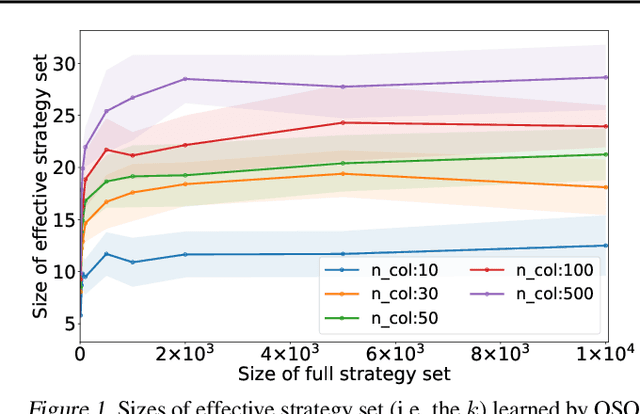
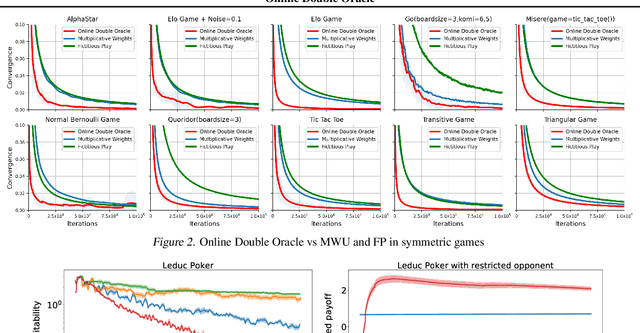
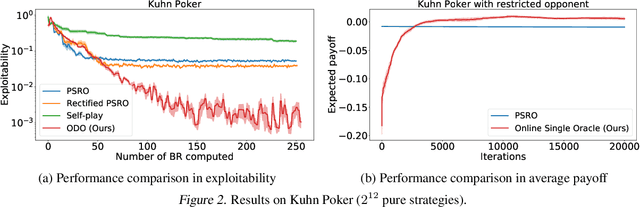
Solving strategic games whose action space is prohibitively large is a critical yet under-explored topic in economics, computer science and artificial intelligence. This paper proposes new learning algorithms in two-player zero-sum games where the number of pure strategies is huge or even infinite. Specifically, we combine no-regret analysis from online learning with double oracle methods from game theory. Our method -- \emph{Online Double Oracle (ODO)} -- achieves the regret bound of $\mathcal{O}(\sqrt{T k \log(k)})$ in self-play setting where $k$ is NOT the size of the game, but rather the size of \emph{effective strategy set} that is linearly dependent on the support size of the Nash equilibrium. On tens of different real-world games, including Leduc Poker that contains $3^{936}$ pure strategies, our methods outperform no-regret algorithms and double oracle methods by a large margin, both in convergence rate to Nash equilibrium and average payoff against strategic adversary.

Exploiting No-Regret Algorithms in System Design

We investigate a repeated two-player zero-sum game setting where the column player is also a designer of the system, and has full control on the design of the payoff matrix. In addition, the row player uses a no-regret algorithm to efficiently learn how to adapt their strategy to the column player's behaviour over time in order to achieve good total payoff. The goal of the column player is to guide her opponent to pick a mixed strategy which is favourable for the system designer. Therefore, she needs to: (i) design an appropriate payoff matrix $A$ whose unique minimax solution contains the desired mixed strategy of the row player; and (ii) strategically interact with the row player during a sequence of plays in order to guide her opponent to converge to that desired behaviour. To design such a payoff matrix, we propose a novel solution that provably has a unique minimax solution with the desired behaviour. We also investigate a relaxation of this problem where uniqueness is not required, but all the minimax solutions have the same mixed strategy for the row player. Finally, we propose a new game playing algorithm for the system designer and prove that it can guide the row player, who may play a \emph{stable} no-regret algorithm, to converge to a minimax solution.