Learning Risk-Averse Equilibria in Multi-Agent Systems
Paper and Code
May 30, 2022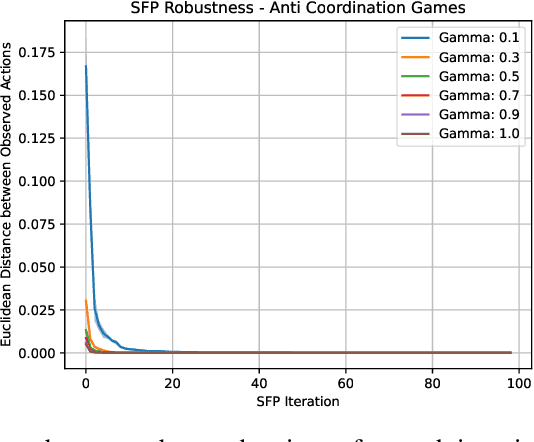
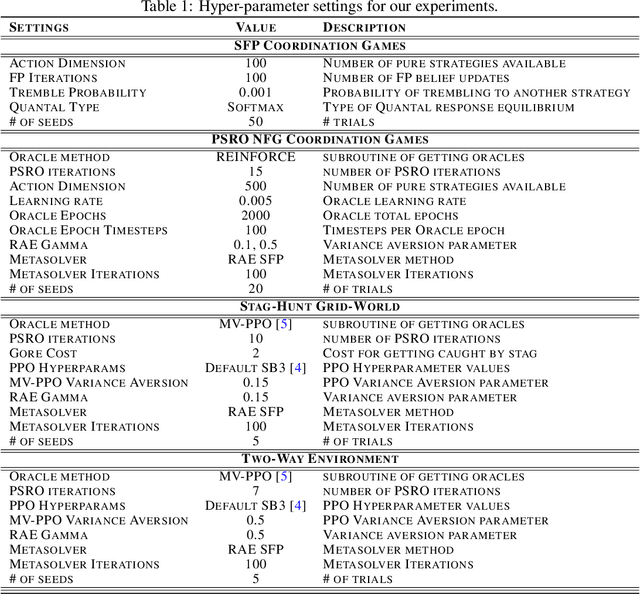
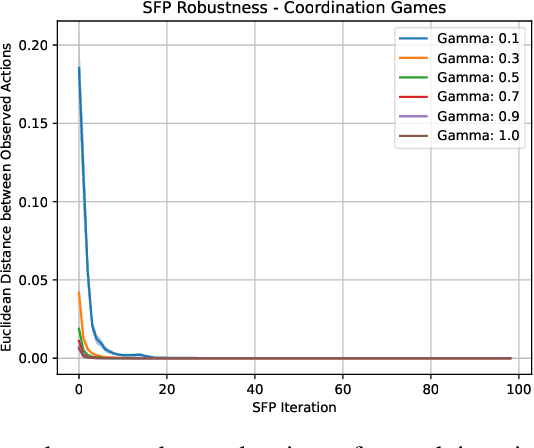
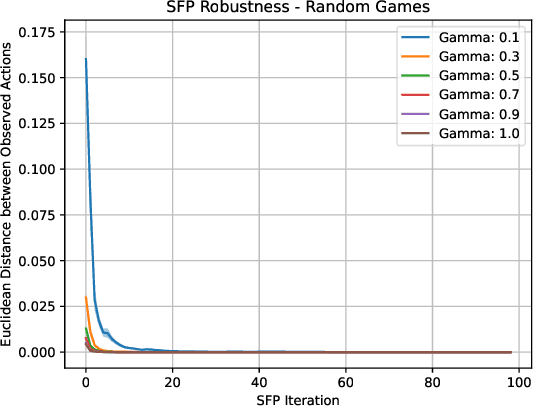
In multi-agent systems, intelligent agents are tasked with making decisions that have optimal outcomes when the actions of the other agents are as expected, whilst also being prepared for unexpected behaviour. In this work, we introduce a new risk-averse solution concept that allows the learner to accommodate unexpected actions by finding the minimum variance strategy given any level of expected return. We prove the existence of such a risk-averse equilibrium, and propose one fictitious-play type learning algorithm for smaller games that enjoys provable convergence guarantees in certain games classes (e.g., zero-sum or potential). Furthermore, we propose an approximation method for larger games based on iterative population-based training that generates a population of risk-averse agents. Empirically, our equilibrium is shown to be able to reduce the reward variance, specifically in the sense that off-equilibrium behaviour has a far smaller impact on our risk-averse agents in comparison to playing other equilibrium solutions. Importantly, we show that our population of agents that approximate a risk-averse equilibrium is particularly effective in the presence of unseen opposing populations, especially in the case of guaranteeing a minimal level of performance which is critical to safety-aware multi-agent systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge