COMAL: A Convergent Meta-Algorithm for Aligning LLMs with General Preferences

Many alignment methods, including reinforcement learning from human feedback (RLHF), rely on the Bradley-Terry reward assumption, which is insufficient to capture the full range of general human preferences. To achieve robust alignment with general preferences, we model the alignment problem as a two-player zero-sum game, where the Nash equilibrium policy guarantees a 50% win rate against any competing policy. However, previous algorithms for finding the Nash policy either diverge or converge to a Nash policy in a modified game, even in a simple synthetic setting, thereby failing to maintain the 50% win rate guarantee against all other policies. We propose a meta-algorithm, Convergent Meta Alignment Algorithm (COMAL), for language model alignment with general preferences, inspired by convergent algorithms in game theory. Theoretically, we prove that our meta-algorithm converges to an exact Nash policy in the last iterate. Additionally, our meta-algorithm is simple and can be integrated with many existing methods designed for RLHF and preference optimization with minimal changes. Experimental results demonstrate the effectiveness of the proposed framework when combined with existing preference policy optimization methods.

Fast Last-Iterate Convergence of Learning in Games Requires Forgetful Algorithms

Self-play via online learning is one of the premier ways to solve large-scale two-player zero-sum games, both in theory and practice. Particularly popular algorithms include optimistic multiplicative weights update (OMWU) and optimistic gradient-descent-ascent (OGDA). While both algorithms enjoy $O(1/T)$ ergodic convergence to Nash equilibrium in two-player zero-sum games, OMWU offers several advantages including logarithmic dependence on the size of the payoff matrix and $\widetilde{O}(1/T)$ convergence to coarse correlated equilibria even in general-sum games. However, in terms of last-iterate convergence in two-player zero-sum games, an increasingly popular topic in this area, OGDA guarantees that the duality gap shrinks at a rate of $O(1/\sqrt{T})$, while the best existing last-iterate convergence for OMWU depends on some game-dependent constant that could be arbitrarily large. This begs the question: is this potentially slow last-iterate convergence an inherent disadvantage of OMWU, or is the current analysis too loose? Somewhat surprisingly, we show that the former is true. More generally, we prove that a broad class of algorithms that do not forget the past quickly all suffer the same issue: for any arbitrarily small $\delta>0$, there exists a $2\times 2$ matrix game such that the algorithm admits a constant duality gap even after $1/\delta$ rounds. This class of algorithms includes OMWU and other standard optimistic follow-the-regularized-leader algorithms.

Tractable Local Equilibria in Non-Concave Games

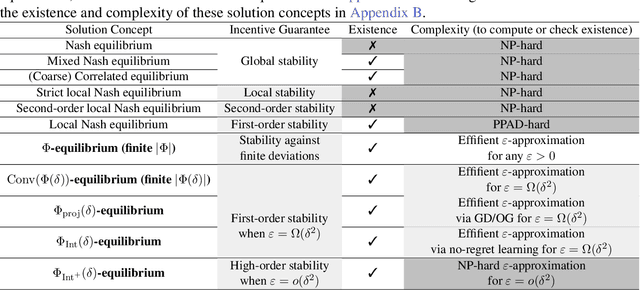
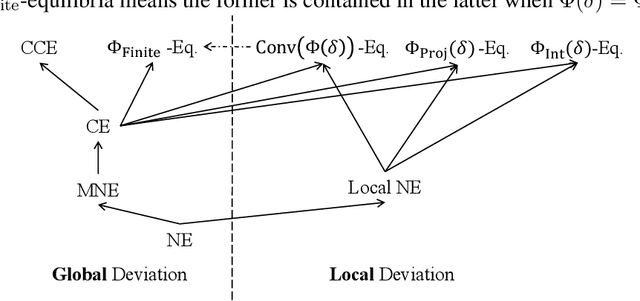
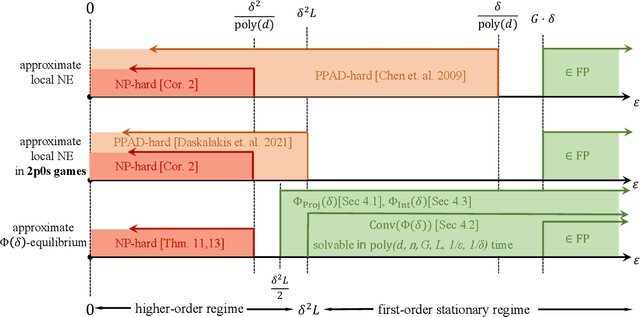
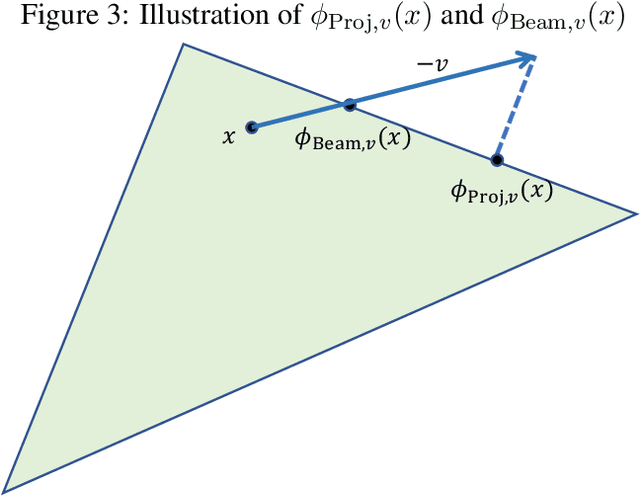
While Online Gradient Descent and other no-regret learning procedures are known to efficiently converge to coarse correlated equilibrium in games where each agent's utility is concave in their own strategy, this is not the case when the utilities are non-concave, a situation that is common in machine learning applications where the agents' strategies are parameterized by deep neural networks, or the agents' utilities are computed by a neural network, or both. Indeed, non-concave games present a host of game-theoretic and optimization challenges: (i) Nash equilibria may fail to exist; (ii) local Nash equilibria exist but are intractable; and (iii) mixed Nash, correlated, and coarse correlated equilibria have infinite support in general, and are intractable. To sidestep these challenges we propose a new solution concept, termed $(\varepsilon, \Phi(\delta))$-local equilibrium, which generalizes local Nash equilibrium in non-concave games, as well as (coarse) correlated equilibrium in concave games. Importantly, we show that two instantiations of this solution concept capture the convergence guarantees of Online Gradient Descent and no-regret learning, which we show efficiently converge to this type of equilibrium in non-concave games with smooth utilities.

Near-Optimal Policy Optimization for Correlated Equilibrium in General-Sum Markov Games

We study policy optimization algorithms for computing correlated equilibria in multi-player general-sum Markov Games. Previous results achieve $O(T^{-1/2})$ convergence rate to a correlated equilibrium and an accelerated $O(T^{-3/4})$ convergence rate to the weaker notion of coarse correlated equilibrium. In this paper, we improve both results significantly by providing an uncoupled policy optimization algorithm that attains a near-optimal $\tilde{O}(T^{-1})$ convergence rate for computing a correlated equilibrium. Our algorithm is constructed by combining two main elements (i) smooth value updates and (ii) the optimistic-follow-the-regularized-leader algorithm with the log barrier regularizer.

Learning Thresholds with Latent Values and Censored Feedback

In this paper, we investigate a problem of actively learning threshold in latent space, where the unknown reward $g(\gamma, v)$ depends on the proposed threshold $\gamma$ and latent value $v$ and it can be $only$ achieved if the threshold is lower than or equal to the unknown latent value. This problem has broad applications in practical scenarios, e.g., reserve price optimization in online auctions, online task assignments in crowdsourcing, setting recruiting bars in hiring, etc. We first characterize the query complexity of learning a threshold with the expected reward at most $\epsilon$ smaller than the optimum and prove that the number of queries needed can be infinitely large even when $g(\gamma, v)$ is monotone with respect to both $\gamma$ and $v$. On the positive side, we provide a tight query complexity $\tilde{\Theta}(1/\epsilon^3)$ when $g$ is monotone and the CDF of value distribution is Lipschitz. Moreover, we show a tight $\tilde{\Theta}(1/\epsilon^3)$ query complexity can be achieved as long as $g$ satisfies one-sided Lipschitzness, which provides a complete characterization for this problem. Finally, we extend this model to an online learning setting and demonstrate a tight $\Theta(T^{2/3})$ regret bound using continuous-arm bandit techniques and the aforementioned query complexity results.

Last-Iterate Convergence Properties of Regret-Matching Algorithms in Games

Algorithms based on regret matching, specifically regret matching$^+$ (RM$^+$), and its variants are the most popular approaches for solving large-scale two-player zero-sum games in practice. Unlike algorithms such as optimistic gradient descent ascent, which have strong last-iterate and ergodic convergence properties for zero-sum games, virtually nothing is known about the last-iterate properties of regret-matching algorithms. Given the importance of last-iterate convergence for numerical optimization reasons and relevance as modeling real-word learning in games, in this paper, we study the last-iterate convergence properties of various popular variants of RM$^+$. First, we show numerically that several practical variants such as simultaneous RM$^+$, alternating RM$^+$, and simultaneous predictive RM$^+$, all lack last-iterate convergence guarantees even on a simple $3\times 3$ game. We then prove that recent variants of these algorithms based on a smoothing technique do enjoy last-iterate convergence: we prove that extragradient RM$^{+}$ and smooth Predictive RM$^+$ enjoy asymptotic last-iterate convergence (without a rate) and $1/\sqrt{t}$ best-iterate convergence. Finally, we introduce restarted variants of these algorithms, and show that they enjoy linear-rate last-iterate convergence.

Uncoupled and Convergent Learning in Two-Player Zero-Sum Markov Games

We revisit the problem of learning in two-player zero-sum Markov games, focusing on developing an algorithm that is $uncoupled$, $convergent$, and $rational$, with non-asymptotic convergence rates. We start from the case of stateless matrix game with bandit feedback as a warm-up, showing an $\mathcal{O}(t^{-\frac{1}{8}})$ last-iterate convergence rate. To the best of our knowledge, this is the first result that obtains finite last-iterate convergence rate given access to only bandit feedback. We extend our result to the case of irreducible Markov games, providing a last-iterate convergence rate of $\mathcal{O}(t^{-\frac{1}{9+\varepsilon}})$ for any $\varepsilon>0$. Finally, we study Markov games without any assumptions on the dynamics, and show a $path convergence$ rate, which is a new notion of convergence we defined, of $\mathcal{O}(t^{-\frac{1}{10}})$. Our algorithm removes the synchronization and prior knowledge requirement of [Wei et al., 2021], which pursued the same goals as us for irreducible Markov games. Our algorithm is related to [Chen et al., 2021, Cen et al., 2021] and also builds on the entropy regularization technique. However, we remove their requirement of communications on the entropy values, making our algorithm entirely uncoupled.

Doubly Optimal No-Regret Learning in Monotone Games

We consider online learning in multi-player smooth monotone games. Existing algorithms have limitations such as (1) being only applicable to strongly monotone games; (2) lacking the no-regret guarantee; (3) having only asymptotic or slow $\mathcal{O}(\frac{1}{\sqrt{T}})$ last-iterate convergence rate to a Nash equilibrium. While the $\mathcal{O}(\frac{1}{\sqrt{T}})$ rate is tight for a large class of algorithms including the well-studied extragradient algorithm and optimistic gradient algorithm, it is not optimal for all gradient-based algorithms. We propose the accelerated optimistic gradient (AOG) algorithm, the first doubly optimal no-regret learning algorithm for smooth monotone games. Namely, our algorithm achieves both (i) the optimal $\mathcal{O}(\sqrt{T})$ regret in the adversarial setting under smooth and convex loss functions and (ii) the optimal $\mathcal{O}(\frac{1}{T})$ last-iterate convergence rate to a Nash equilibrium in multi-player smooth monotone games. As a byproduct of the accelerated last-iterate convergence rate, we further show that each player suffers only an $\mathcal{O}(\log T)$ individual worst-case dynamic regret, providing an exponential improvement over the previous state-of-the-art $\mathcal{O}(\sqrt{T})$ bound.

Accelerated Single-Call Methods for Constrained Min-Max Optimization

We study first-order methods for constrained min-max optimization. Existing methods either requires two gradient calls or two projections in each iteration, which may be costly in applications. In this paper, we first show that the Optimistic Gradient (OG) method, a single-call single-projection algorithm, has $O(\frac{1}{\sqrt{T}})$ convergence rate for inclusion problems with operators that satisfy the weak Minty variation inequality (MVI). Our second result is the first single-call single-projection algorithm -- the Accelerated Reflected Gradient (ARG) method that achieves the optimal $O(\frac{1}{T})$ convergence rate for inclusion problems that satisfy negative comonotonicity. Both the weak MVI and negative comonotonicity are well-studied assumptions and capture a rich set of non-convex non-concave min-max optimization problems. Finally, we show that the Reflected Gradient (RG) method, another single-call single-projection algorithm, has $O(\frac{1}{\sqrt{T}})$ last-iterate convergence rate for constrained convex-concave min-max optimization, answering an open problem of [Hsieh et al, 2019].

Accelerated Algorithms for Monotone Inclusions and Constrained Nonconvex-Nonconcave Min-Max Optimization

We study monotone inclusions and monotone variational inequalities, as well as their generalizations to non-monotone settings. We first show that the Extra Anchored Gradient (EAG) algorithm, originally proposed by Yoon and Ryu [2021] for unconstrained convex-concave min-max optimization, can be applied to solve the more general problem of Lipschitz monotone inclusion. More specifically, we prove that the EAG solves Lipschitz monotone inclusion problems with an \emph{accelerated convergence rate} of $O(\frac{1}{T})$, which is \emph{optimal among all first-order methods} [Diakonikolas, 2020, Yoon and Ryu, 2021]. Our second result is a new algorithm, called Extra Anchored Gradient Plus (EAG+), which not only achieves the accelerated $O(\frac{1}{T})$ convergence rate for all monotone inclusion problems, but also exhibits the same accelerated rate for a family of general (non-monotone) inclusion problems that concern negative comonotone operators. As a special case of our second result, EAG+ enjoys the $O(\frac{1}{T})$ convergence rate for solving a non-trivial class of nonconvex-nonconcave min-max optimization problems. Our analyses are based on simple potential function arguments, which might be useful for analysing other accelerated algorithms.