Stationary Policies are Optimal in Risk-averse Total-reward MDPs with EVaR

Optimizing risk-averse objectives in discounted MDPs is challenging because most models do not admit direct dynamic programming equations and require complex history-dependent policies. In this paper, we show that the risk-averse {\em total reward criterion}, under the Entropic Risk Measure (ERM) and Entropic Value at Risk (EVaR) risk measures, can be optimized by a stationary policy, making it simple to analyze, interpret, and deploy. We propose exponential value iteration, policy iteration, and linear programming to compute optimal policies. In comparison with prior work, our results only require the relatively mild condition of transient MDPs and allow for {\em both} positive and negative rewards. Our results indicate that the total reward criterion may be preferable to the discounted criterion in a broad range of risk-averse reinforcement learning domains.

Fast Last-Iterate Convergence of Learning in Games Requires Forgetful Algorithms

Self-play via online learning is one of the premier ways to solve large-scale two-player zero-sum games, both in theory and practice. Particularly popular algorithms include optimistic multiplicative weights update (OMWU) and optimistic gradient-descent-ascent (OGDA). While both algorithms enjoy $O(1/T)$ ergodic convergence to Nash equilibrium in two-player zero-sum games, OMWU offers several advantages including logarithmic dependence on the size of the payoff matrix and $\widetilde{O}(1/T)$ convergence to coarse correlated equilibria even in general-sum games. However, in terms of last-iterate convergence in two-player zero-sum games, an increasingly popular topic in this area, OGDA guarantees that the duality gap shrinks at a rate of $O(1/\sqrt{T})$, while the best existing last-iterate convergence for OMWU depends on some game-dependent constant that could be arbitrarily large. This begs the question: is this potentially slow last-iterate convergence an inherent disadvantage of OMWU, or is the current analysis too loose? Somewhat surprisingly, we show that the former is true. More generally, we prove that a broad class of algorithms that do not forget the past quickly all suffer the same issue: for any arbitrarily small $\delta>0$, there exists a $2\times 2$ matrix game such that the algorithm admits a constant duality gap even after $1/\delta$ rounds. This class of algorithms includes OMWU and other standard optimistic follow-the-regularized-leader algorithms.

Last-Iterate Convergence Properties of Regret-Matching Algorithms in Games

Algorithms based on regret matching, specifically regret matching$^+$ (RM$^+$), and its variants are the most popular approaches for solving large-scale two-player zero-sum games in practice. Unlike algorithms such as optimistic gradient descent ascent, which have strong last-iterate and ergodic convergence properties for zero-sum games, virtually nothing is known about the last-iterate properties of regret-matching algorithms. Given the importance of last-iterate convergence for numerical optimization reasons and relevance as modeling real-word learning in games, in this paper, we study the last-iterate convergence properties of various popular variants of RM$^+$. First, we show numerically that several practical variants such as simultaneous RM$^+$, alternating RM$^+$, and simultaneous predictive RM$^+$, all lack last-iterate convergence guarantees even on a simple $3\times 3$ game. We then prove that recent variants of these algorithms based on a smoothing technique do enjoy last-iterate convergence: we prove that extragradient RM$^{+}$ and smooth Predictive RM$^+$ enjoy asymptotic last-iterate convergence (without a rate) and $1/\sqrt{t}$ best-iterate convergence. Finally, we introduce restarted variants of these algorithms, and show that they enjoy linear-rate last-iterate convergence.

Regret Matching+: (In)Stability and Fast Convergence in Games

Regret Matching+ (RM+) and its variants are important algorithms for solving large-scale games. However, a theoretical understanding of their success in practice is still a mystery. Moreover, recent advances on fast convergence in games are limited to no-regret algorithms such as online mirror descent, which satisfy stability. In this paper, we first give counterexamples showing that RM+ and its predictive version can be unstable, which might cause other players to suffer large regret. We then provide two fixes: restarting and chopping off the positive orthant that RM+ works in. We show that these fixes are sufficient to get $O(T^{1/4})$ individual regret and $O(1)$ social regret in normal-form games via RM+ with predictions. We also apply our stabilizing techniques to clairvoyant updates in the uncoupled learning setting for RM+ and prove desirable results akin to recent works for Clairvoyant online mirror descent. Our experiments show the advantages of our algorithms over vanilla RM+-based algorithms in matrix and extensive-form games.

Reducing Blackwell and Average Optimality to Discounted MDPs via the Blackwell Discount Factor

We introduce the Blackwell discount factor for Markov Decision Processes (MDPs). Classical objectives for MDPs include discounted, average, and Blackwell optimality. Many existing approaches to computing average-optimal policies solve for discounted optimal policies with a discount factor close to $1$, but they only work under strong or hard-to-verify assumptions such as ergodicity or weakly communicating MDPs. In this paper, we show that when the discount factor is larger than the Blackwell discount factor $\gamma_{\mathrm{bw}}$, all discounted optimal policies become Blackwell- and average-optimal, and we derive a general upper bound on $\gamma_{\mathrm{bw}}$. The upper bound on $\gamma_{\mathrm{bw}}$ provides the first reduction from average and Blackwell optimality to discounted optimality, without any assumptions, and new polynomial-time algorithms for average- and Blackwell-optimal policies. Our work brings new ideas from the study of polynomials and algebraic numbers to the analysis of MDPs. Our results also apply to robust MDPs, enabling the first algorithms to compute robust Blackwell-optimal policies.

On the convex formulations of robust Markov decision processes

Robust Markov decision processes (MDPs) are used for applications of dynamic optimization in uncertain environments and have been studied extensively. Many of the main properties and algorithms of MDPs, such as value iteration and policy iteration, extend directly to RMDPs. Surprisingly, there is no known analog of the MDP convex optimization formulation for solving RMDPs. This work describes the first convex optimization formulation of RMDPs under the classical sa-rectangularity and s-rectangularity assumptions. We derive a convex formulation with a linear number of variables and constraints but large coefficients in the constraints by using entropic regularization and exponential change of variables. Our formulation can be combined with efficient methods from convex optimization to obtain new algorithms for solving RMDPs with uncertain probabilities. We further simplify the formulation for RMDPs with polyhedral uncertainty sets. Our work opens a new research direction for RMDPs and can serve as a first step toward obtaining a tractable convex formulation of RMDPs.

The Best Decisions Are Not the Best Advice: Making Adherence-Aware Recommendations

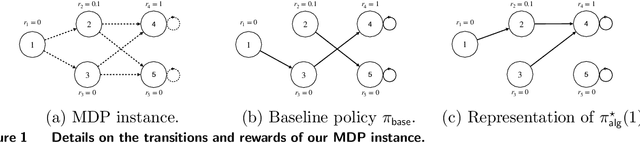
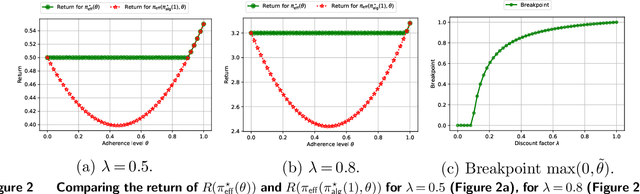
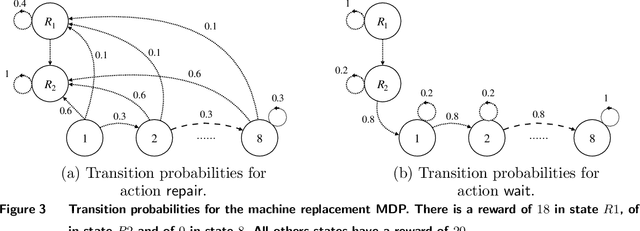
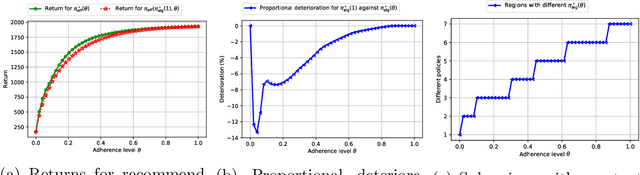
Many high-stake decisions follow an expert-in-loop structure in that a human operator receives recommendations from an algorithm but is the ultimate decision maker. Hence, the algorithm's recommendation may differ from the actual decision implemented in practice. However, most algorithmic recommendations are obtained by solving an optimization problem that assumes recommendations will be perfectly implemented. We propose an adherence-aware optimization framework to capture the dichotomy between the recommended and the implemented policy and analyze the impact of partial adherence on the optimal recommendation. We show that overlooking the partial adherence phenomenon, as is currently being done by most recommendation engines, can lead to arbitrarily severe performance deterioration, compared with both the current human baseline performance and what is expected by the recommendation algorithm. Our framework also provides useful tools to analyze the structure and to compute optimal recommendation policies that are naturally immune against such human deviations, and are guaranteed to improve upon the baseline policy.

Solving optimization problems with Blackwell approachability

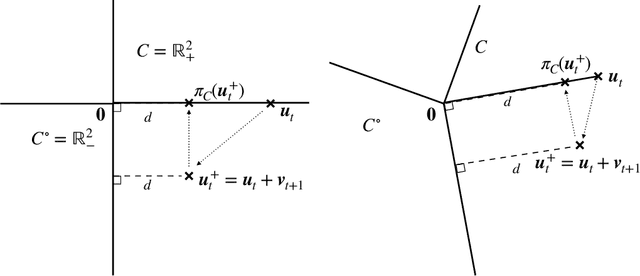
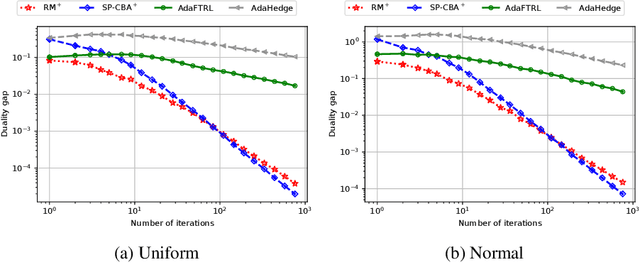
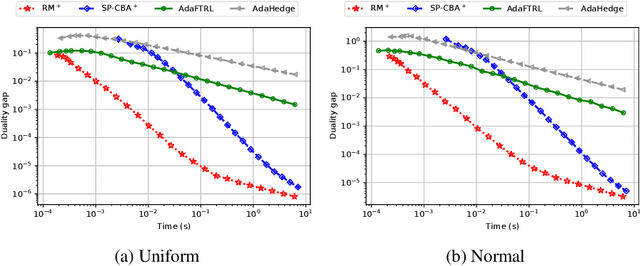
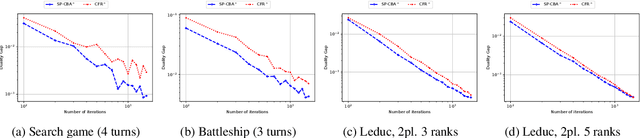
We introduce the Conic Blackwell Algorithm$^+$ (CBA$^+$) regret minimizer, a new parameter- and scale-free regret minimizer for general convex sets. CBA$^+$ is based on Blackwell approachability and attains $O(\sqrt{T})$ regret. We show how to efficiently instantiate CBA$^+$ for many decision sets of interest, including the simplex, $\ell_{p}$ norm balls, and ellipsoidal confidence regions in the simplex. Based on CBA$^+$, we introduce SP-CBA$^+$, a new parameter-free algorithm for solving convex-concave saddle-point problems, which achieves a $O(1/\sqrt{T})$ ergodic rate of convergence. In our simulations, we demonstrate the wide applicability of SP-CBA$^+$ on several standard saddle-point problems, including matrix games, extensive-form games, distributionally robust logistic regression, and Markov decision processes. In each setting, SP-CBA$^+$ achieves state-of-the-art numerical performance, and outperforms classical methods, without the need for any choice of step sizes or other algorithmic parameters.

Interpretable Machine Learning for Resource Allocation with Application to Ventilator Triage

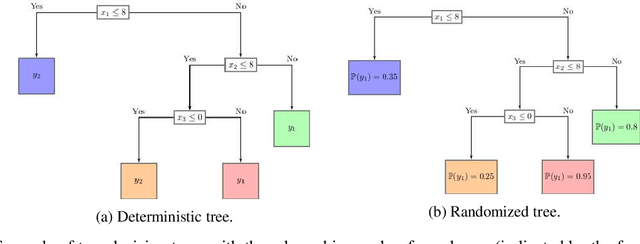
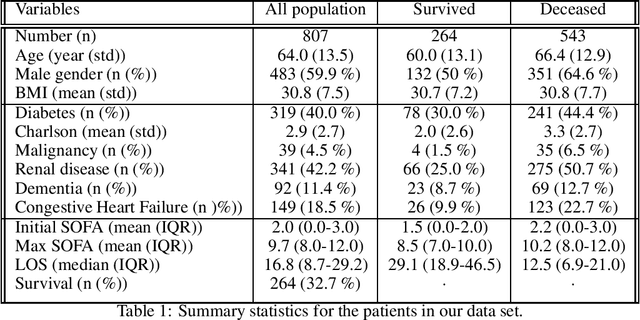
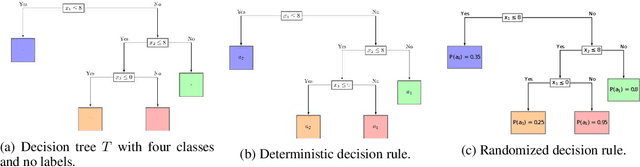
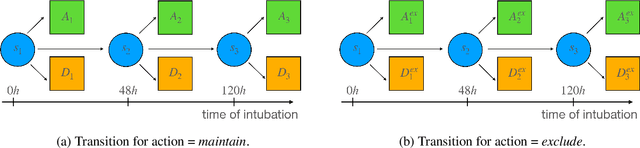
Rationing of healthcare resources is a challenging decision that policy makers and providers may be forced to make during a pandemic, natural disaster, or mass casualty event. Well-defined guidelines to triage scarce life-saving resources must be designed to promote transparency, trust, and consistency. To facilitate buy-in and use during high-stress situations, these guidelines need to be interpretable and operational. We propose a novel data-driven model to compute interpretable triage guidelines based on policies for Markov Decision Process that can be represented as simple sequences of decision trees ("tree policies"). In particular, we characterize the properties of optimal tree policies and present an algorithm based on dynamic programming recursions to compute good tree policies. We utilize this methodology to obtain simple, novel triage guidelines for ventilator allocations for COVID-19 patients, based on real patient data from Montefiore hospitals. We also compare the performance of our guidelines to the official New York State guidelines that were developed in 2015 (well before the COVID-19 pandemic). Our empirical study shows that the number of excess deaths associated with ventilator shortages could be reduced significantly using our policy. Our work highlights the limitations of the existing official triage guidelines, which need to be adapted specifically to COVID-19 before being successfully deployed.

Conic Blackwell Algorithm: Parameter-Free Convex-Concave Saddle-Point Solving

We develop new parameter and scale-free algorithms for solving convex-concave saddle-point problems. Our results are based on a new simple regret minimizer, the Conic Blackwell Algorithm$^+$ (CBA$^+$), which attains $O(1/\sqrt{T})$ average regret. Intuitively, our approach generalizes to other decision sets of interest ideas from the Counterfactual Regret minimization (CFR$^+$) algorithm, which has very strong practical performance for solving sequential games on simplexes. We show how to implement CBA$^+$ for the simplex, $\ell_{p}$ norm balls, and ellipsoidal confidence regions in the simplex, and we present numerical experiments for solving matrix games and distributionally robust optimization problems. Our empirical results show that CBA$^+$ is a simple algorithm that outperforms state-of-the-art methods on synthetic data and real data instances, without the need for any choice of step sizes or other algorithmic parameters.