Adaptive Optimization for Prediction with Missing Data

When training predictive models on data with missing entries, the most widely used and versatile approach is a pipeline technique where we first impute missing entries and then compute predictions. In this paper, we view prediction with missing data as a two-stage adaptive optimization problem and propose a new class of models, adaptive linear regression models, where the regression coefficients adapt to the set of observed features. We show that some adaptive linear regression models are equivalent to learning an imputation rule and a downstream linear regression model simultaneously instead of sequentially. We leverage this joint-impute-then-regress interpretation to generalize our framework to non-linear models. In settings where data is strongly not missing at random, our methods achieve a 2-10% improvement in out-of-sample accuracy.

Patient Outcome Predictions Improve Operations at a Large Hospital Network

Problem definition: Access to accurate predictions of patients' outcomes can enhance medical staff's decision-making, which ultimately benefits all stakeholders in the hospitals. A large hospital network in the US has been collaborating with academics and consultants to predict short-term and long-term outcomes for all inpatients across their seven hospitals. Methodology/results: We develop machine learning models that predict the probabilities of next 24-hr/48-hr discharge and intensive care unit transfers, end-of-stay mortality and discharge dispositions. All models achieve high out-of-sample AUC (75.7%-92.5%) and are well calibrated. In addition, combining 48-hr discharge predictions with doctors' predictions simultaneously enables more patient discharges (10%-28.7%) and fewer 7-day/30-day readmissions ($p$-value $<0.001$). We implement an automated pipeline that extracts data and updates predictions every morning, as well as user-friendly software and a color-coded alert system to communicate these patient-level predictions (alongside explanations) to clinical teams. Managerial implications: Since we have been gradually deploying the tool, and training medical staff, over 200 doctors, nurses, and case managers across seven hospitals use it in their daily patient review process. We observe a significant reduction in the average length of stay (0.67 days per patient) following its adoption and anticipate substantial financial benefits (between \$55 and \$72 million annually) for the healthcare system.

Optimal Low-Rank Matrix Completion: Semidefinite Relaxations and Eigenvector Disjunctions

Low-rank matrix completion consists of computing a matrix of minimal complexity that recovers a given set of observations as accurately as possible, and has numerous applications such as product recommendation. Unfortunately, existing methods for solving low-rank matrix completion are heuristics that, while highly scalable and often identifying high-quality solutions, do not possess any optimality guarantees. We reexamine matrix completion with an optimality-oriented eye, by reformulating low-rank problems as convex problems over the non-convex set of projection matrices and implementing a disjunctive branch-and-bound scheme that solves them to certifiable optimality. Further, we derive a novel and often tight class of convex relaxations by decomposing a low-rank matrix as a sum of rank-one matrices and incentivizing, via a Shor relaxation, that each two-by-two minor in each rank-one matrix has determinant zero. In numerical experiments, our new convex relaxations decrease the optimality gap by two orders of magnitude compared to existing attempts. Moreover, we showcase the performance of our disjunctive branch-and-bound scheme and demonstrate that it solves matrix completion problems over 150x150 matrices to certifiable optimality in hours, constituting an order of magnitude improvement on the state-of-the-art for certifiably optimal methods.

Sparse PCA With Multiple Components

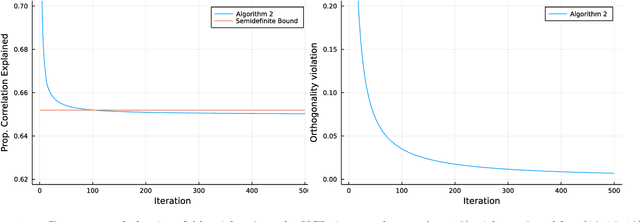
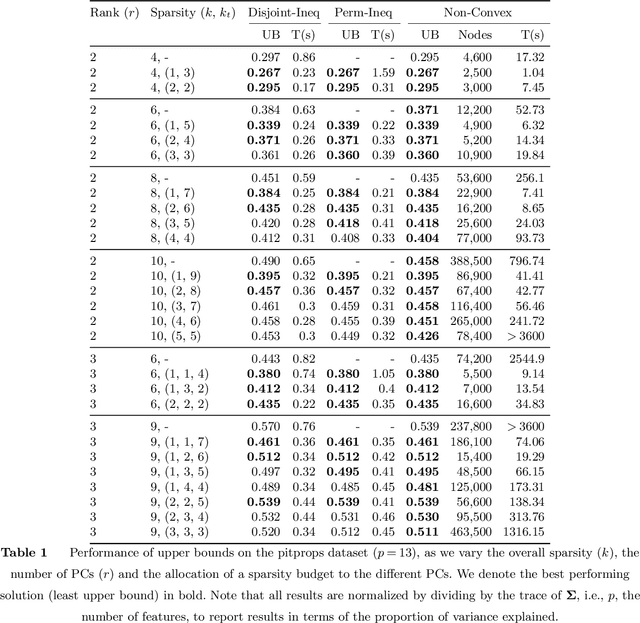
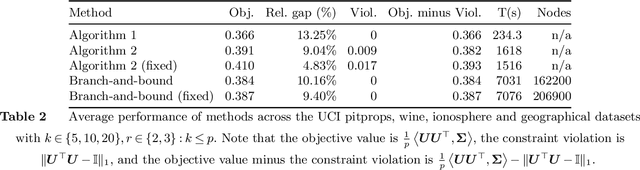
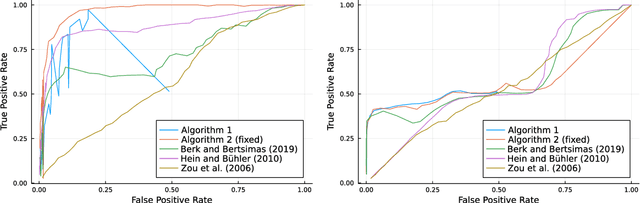
Sparse Principal Component Analysis is a cardinal technique for obtaining combinations of features, or principal components (PCs), that explain the variance of high-dimensional datasets in an interpretable manner. At its heart, this involves solving a sparsity and orthogonality constrained convex maximization problem, which is extremely computationally challenging. Most existing work address sparse PCA via heuristics such as iteratively computing one sparse PC and deflating the covariance matrix, which does not guarantee the orthogonality, let alone the optimality, of the resulting solution. We challenge this status by reformulating the orthogonality conditions as rank constraints and optimizing over the sparsity and rank constraints simultaneously. We design tight semidefinite relaxations and propose tractable second-order cone versions of these relaxations which supply high-quality upper bounds. We also design valid second-order cone inequalities which hold when each PC's individual sparsity is specified, and demonstrate that these inequalities tighten our relaxations significantly. Moreover, we propose exact methods and rounding mechanisms that exploit these relaxations' tightness to obtain solutions with a bound gap on the order of 1%-5% for real-world datasets with p = 100s or 1000s of features and r \in {2, 3} components. We investigate the performance of our methods in spiked covariance settings and demonstrate that simultaneously considering the orthogonality and sparsity constraints leads to improvements in the Area Under the ROC curve of 2%-8% compared to state-of-the-art deflation methods. All in all, our approach solves sparse PCA problems with multiple components to certifiable (near) optimality in a practically tractable fashion.

The Best Decisions Are Not the Best Advice: Making Adherence-Aware Recommendations

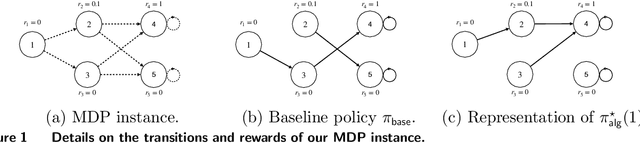
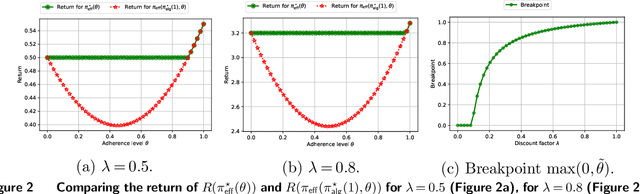
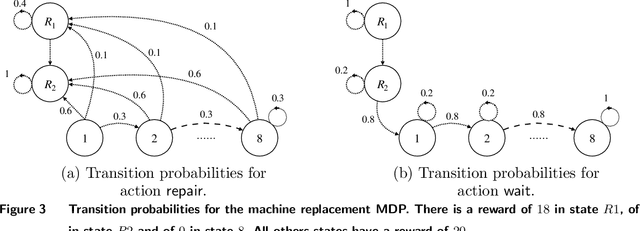
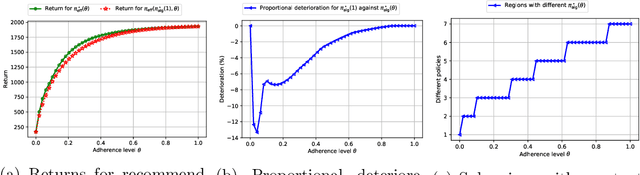
Many high-stake decisions follow an expert-in-loop structure in that a human operator receives recommendations from an algorithm but is the ultimate decision maker. Hence, the algorithm's recommendation may differ from the actual decision implemented in practice. However, most algorithmic recommendations are obtained by solving an optimization problem that assumes recommendations will be perfectly implemented. We propose an adherence-aware optimization framework to capture the dichotomy between the recommended and the implemented policy and analyze the impact of partial adherence on the optimal recommendation. We show that overlooking the partial adherence phenomenon, as is currently being done by most recommendation engines, can lead to arbitrarily severe performance deterioration, compared with both the current human baseline performance and what is expected by the recommendation algorithm. Our framework also provides useful tools to analyze the structure and to compute optimal recommendation policies that are naturally immune against such human deviations, and are guaranteed to improve upon the baseline policy.

Robust and Heterogenous Odds Ratio: Estimating Price Sensitivity for Unbought Items

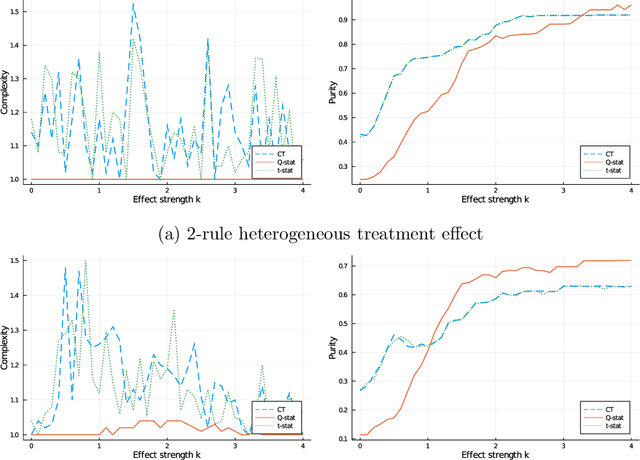
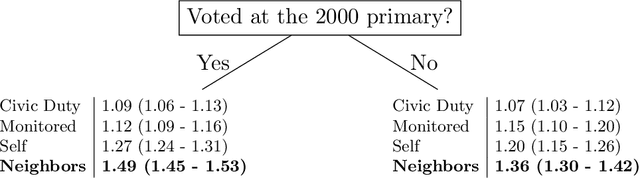
Problem definition: Mining for heterogeneous responses to an intervention is a crucial step for data-driven operations, for instance to personalize treatment or pricing. We investigate how to estimate price sensitivity from transaction-level data. In causal inference terms, we estimate heterogeneous treatment effects when (a) the response to treatment (here, whether a customer buys a product) is binary, and (b) treatment assignments are partially observed (here, full information is only available for purchased items). Methodology/Results: We propose a recursive partitioning procedure to estimate heterogeneous odds ratio, a widely used measure of treatment effect in medicine and social sciences. We integrate an adversarial imputation step to allow for robust inference even in presence of partially observed treatment assignments. We validate our methodology on synthetic data and apply it to three case studies from political science, medicine, and revenue management. Managerial Implications: Our robust heterogeneous odds ratio estimation method is a simple and intuitive tool to quantify heterogeneity in patients or customers and personalize interventions, while lifting a central limitation in many revenue management data.

A new perspective on low-rank optimization

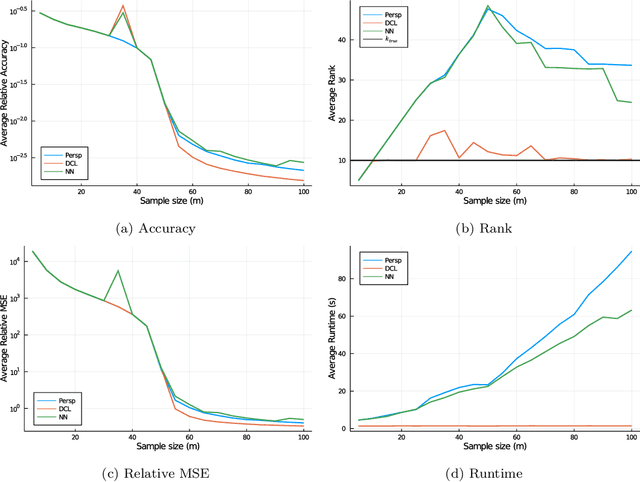
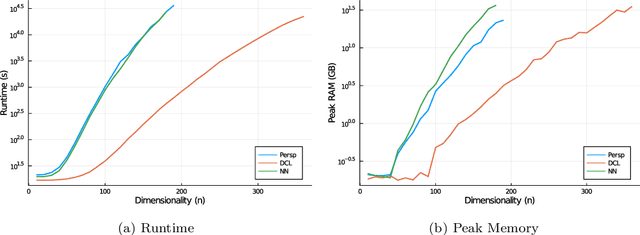
A key question in many low-rank problems throughout optimization, machine learning, and statistics is to characterize the convex hulls of simple low-rank sets and judiciously apply these convex hulls to obtain strong yet computationally tractable convex relaxations. We invoke the matrix perspective function - the matrix analog of the perspective function-and characterize explicitly the convex hull of epigraphs of convex quadratic, matrix exponential, and matrix power functions under low-rank constraints. Further, we exploit these characterizations to develop strong relaxations for a variety of low-rank problems including reduced rank regression, non-negative matrix factorization, and factor analysis. We establish that these relaxations can be modeled via semidefinite and matrix power cone constraints, and thus optimized over tractably. The proposed approach parallels and generalizes the perspective reformulation technique in mixed-integer optimization, and leads to new relaxations for a broad class of problems.

Prediction with Missing Data

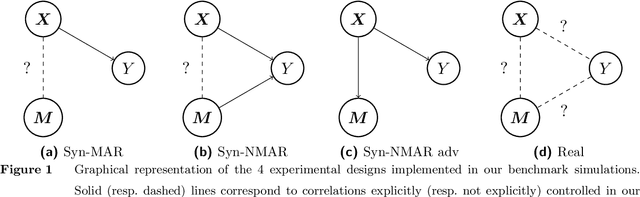
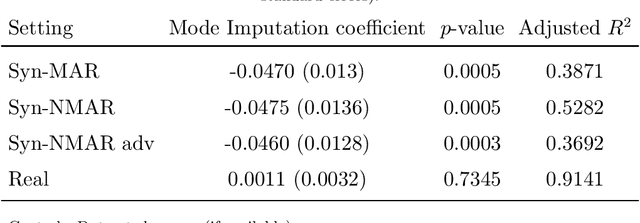
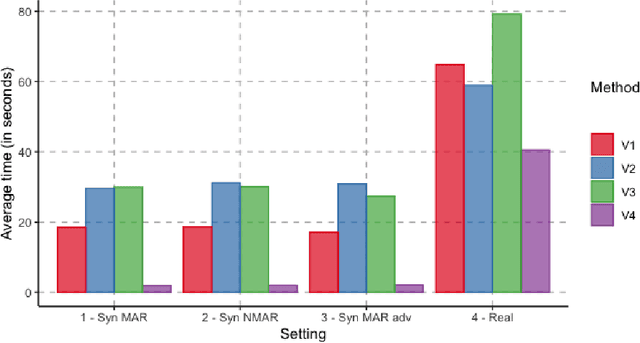
Missing information is inevitable in real-world data sets. While imputation is well-suited and theoretically sound for statistical inference, its relevance and practical implementation for out-of-sample prediction remains unsettled. We provide a theoretical analysis of widely used data imputation methods and highlight their key deficiencies in making accurate predictions. Alternatively, we propose adaptive linear regression, a new class of models that can be directly trained and evaluated on partially observed data, adapting to the set of available features. In particular, we show that certain adaptive regression models are equivalent to impute-then-regress methods where the imputation and the regression models are learned simultaneously instead of sequentially. We validate our theoretical findings and adaptive regression approach with numerical results with real-world data sets.

Mixed-Projection Conic Optimization: A New Paradigm for Modeling Rank Constraints

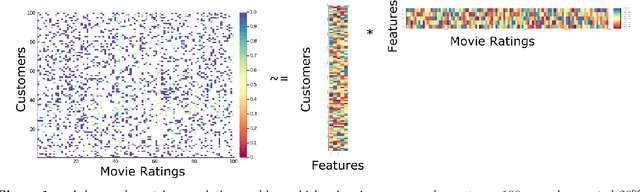
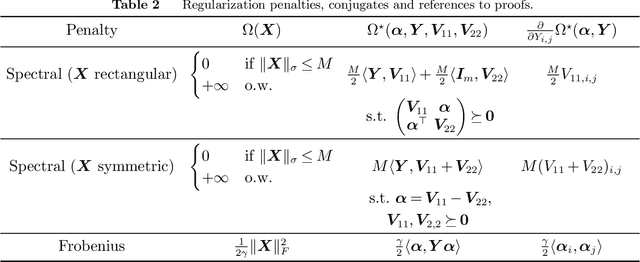
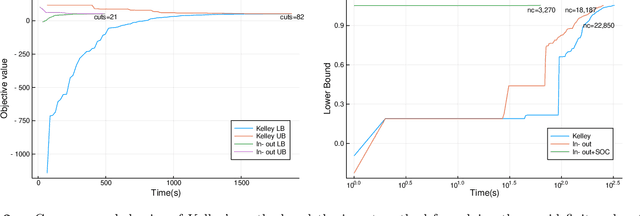
We propose a framework for modeling and solving low-rank optimization problems to certifiable optimality. We introduce symmetric projection matrices that satisfy $Y^2=Y$, the matrix analog of binary variables that satisfy $z^2=z$, to model rank constraints. By leveraging regularization and strong duality, we prove that this modeling paradigm yields tractable convex optimization problems over the non-convex set of orthogonal projection matrices. Furthermore, we design outer-approximation algorithms to solve low-rank problems to certifiable optimality, compute lower bounds via their semidefinite relaxations, and provide near optimal solutions through rounding and local search techniques. We implement these numerical ingredients and, for the first time, solve low-rank optimization problems to certifiable optimality. Our algorithms also supply certifiably near-optimal solutions for larger problem sizes and outperform existing heuristics, by deriving an alternative to the popular nuclear norm relaxation which generalizes the perspective relaxation from vectors to matrices. All in all, our framework, which we name Mixed-Projection Conic Optimization, solves low-rank problems to certifiable optimality in a tractable and unified fashion.

From predictions to prescriptions: A data-driven response to COVID-19

The COVID-19 pandemic has created unprecedented challenges worldwide. Strained healthcare providers make difficult decisions on patient triage, treatment and care management on a daily basis. Policy makers have imposed social distancing measures to slow the disease, at a steep economic price. We design analytical tools to support these decisions and combat the pandemic. Specifically, we propose a comprehensive data-driven approach to understand the clinical characteristics of COVID-19, predict its mortality, forecast its evolution, and ultimately alleviate its impact. By leveraging cohort-level clinical data, patient-level hospital data, and census-level epidemiological data, we develop an integrated four-step approach, combining descriptive, predictive and prescriptive analytics. First, we aggregate hundreds of clinical studies into the most comprehensive database on COVID-19 to paint a new macroscopic picture of the disease. Second, we build personalized calculators to predict the risk of infection and mortality as a function of demographics, symptoms, comorbidities, and lab values. Third, we develop a novel epidemiological model to project the pandemic's spread and inform social distancing policies. Fourth, we propose an optimization model to re-allocate ventilators and alleviate shortages. Our results have been used at the clinical level by several hospitals to triage patients, guide care management, plan ICU capacity, and re-distribute ventilators. At the policy level, they are currently supporting safe back-to-work policies at a major institution and equitable vaccine distribution planning at a major pharmaceutical company, and have been integrated into the US Center for Disease Control's pandemic forecast.