AI Hilbert: From Data and Background Knowledge to Automated Scientific Discovery

The discovery of scientific formulae that parsimoniously explain natural phenomena and align with existing background theory is a key goal in science. Historically, scientists have derived natural laws by manipulating equations based on existing knowledge, forming new equations, and verifying them experimentally. In recent years, data-driven scientific discovery has emerged as a viable competitor in settings with large amounts of experimental data. Unfortunately, data-driven methods often fail to discover valid laws when data is noisy or scarce. Accordingly, recent works combine regression and reasoning to eliminate formulae inconsistent with background theory. However, the problem of searching over the space of formulae consistent with background theory to find one that fits the data best is not well solved. We propose a solution to this problem when all axioms and scientific laws are expressible via polynomial equalities and inequalities and argue that our approach is widely applicable. We further model notions of minimal complexity using binary variables and logical constraints, solve polynomial optimization problems via mixed-integer linear or semidefinite optimization, and automatically prove the validity of our scientific discoveries via Positivestellensatz certificates. Remarkably, the optimization techniques leveraged in this paper allow our approach to run in polynomial time with fully correct background theory, or non-deterministic polynomial (NP) time with partially correct background theory. We experimentally demonstrate that some famous scientific laws, including Kepler's Third Law of Planetary Motion, the Hagen-Poiseuille Equation, and the Radiated Gravitational Wave Power equation, can be automatically derived from sets of partially correct background axioms.

Gain Confidence, Reduce Disappointment: A New Approach to Cross-Validation for Sparse Regression

Ridge regularized sparse regression involves selecting a subset of features that explains the relationship between a design matrix and an output vector in an interpretable manner. To select the sparsity and robustness of linear regressors, techniques like leave-one-out cross-validation are commonly used for hyperparameter tuning. However, cross-validation typically increases the cost of sparse regression by several orders of magnitude. Additionally, validation metrics are noisy estimators of the test-set error, with different hyperparameter combinations giving models with different amounts of noise. Therefore, optimizing over these metrics is vulnerable to out-of-sample disappointment, especially in underdetermined settings. To address this, we make two contributions. First, we leverage the generalization theory literature to propose confidence-adjusted variants of leave-one-out that display less propensity to out-of-sample disappointment. Second, we leverage ideas from the mixed-integer literature to obtain computationally tractable relaxations of confidence-adjusted leave-one-out, thereby minimizing it without solving as many MIOs. Our relaxations give rise to an efficient coordinate descent scheme which allows us to obtain significantly lower leave-one-out errors than via other methods in the literature. We validate our theory by demonstrating we obtain significantly sparser and comparably accurate solutions than via popular methods like GLMNet and suffer from less out-of-sample disappointment. On synthetic datasets, our confidence adjustment procedure generates significantly fewer false discoveries, and improves out-of-sample performance by 2-5% compared to cross-validating without confidence adjustment. Across a suite of 13 real datasets, a calibrated version of our procedure improves the test set error by an average of 4% compared to cross-validating without confidence adjustment.

Optimal Low-Rank Matrix Completion: Semidefinite Relaxations and Eigenvector Disjunctions

Low-rank matrix completion consists of computing a matrix of minimal complexity that recovers a given set of observations as accurately as possible, and has numerous applications such as product recommendation. Unfortunately, existing methods for solving low-rank matrix completion are heuristics that, while highly scalable and often identifying high-quality solutions, do not possess any optimality guarantees. We reexamine matrix completion with an optimality-oriented eye, by reformulating low-rank problems as convex problems over the non-convex set of projection matrices and implementing a disjunctive branch-and-bound scheme that solves them to certifiable optimality. Further, we derive a novel and often tight class of convex relaxations by decomposing a low-rank matrix as a sum of rank-one matrices and incentivizing, via a Shor relaxation, that each two-by-two minor in each rank-one matrix has determinant zero. In numerical experiments, our new convex relaxations decrease the optimality gap by two orders of magnitude compared to existing attempts. Moreover, we showcase the performance of our disjunctive branch-and-bound scheme and demonstrate that it solves matrix completion problems over 150x150 matrices to certifiable optimality in hours, constituting an order of magnitude improvement on the state-of-the-art for certifiably optimal methods.

Sparse PCA With Multiple Components

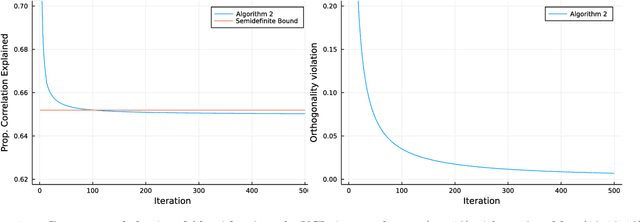
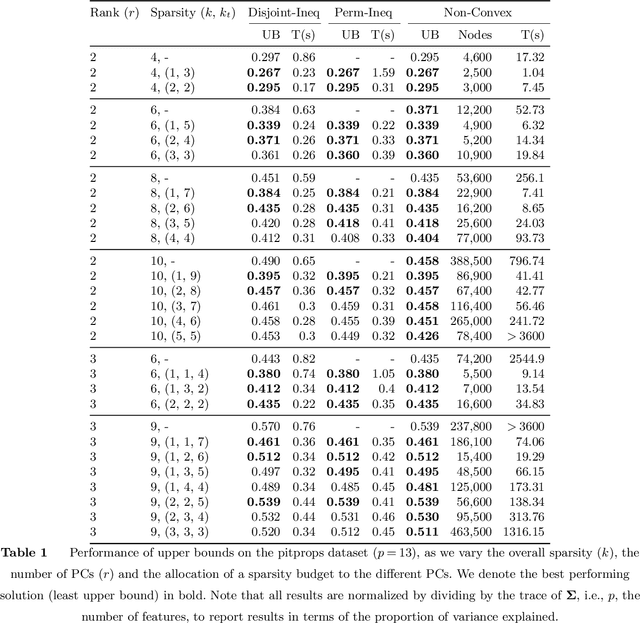
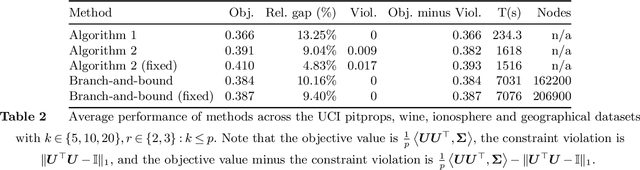
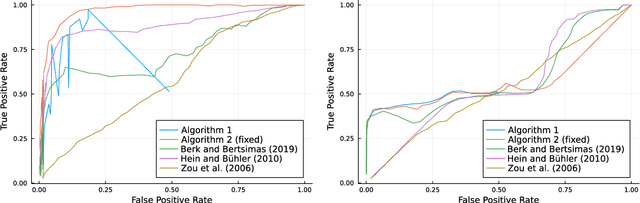
Sparse Principal Component Analysis is a cardinal technique for obtaining combinations of features, or principal components (PCs), that explain the variance of high-dimensional datasets in an interpretable manner. At its heart, this involves solving a sparsity and orthogonality constrained convex maximization problem, which is extremely computationally challenging. Most existing work address sparse PCA via heuristics such as iteratively computing one sparse PC and deflating the covariance matrix, which does not guarantee the orthogonality, let alone the optimality, of the resulting solution. We challenge this status by reformulating the orthogonality conditions as rank constraints and optimizing over the sparsity and rank constraints simultaneously. We design tight semidefinite relaxations and propose tractable second-order cone versions of these relaxations which supply high-quality upper bounds. We also design valid second-order cone inequalities which hold when each PC's individual sparsity is specified, and demonstrate that these inequalities tighten our relaxations significantly. Moreover, we propose exact methods and rounding mechanisms that exploit these relaxations' tightness to obtain solutions with a bound gap on the order of 1%-5% for real-world datasets with p = 100s or 1000s of features and r \in {2, 3} components. We investigate the performance of our methods in spiked covariance settings and demonstrate that simultaneously considering the orthogonality and sparsity constraints leads to improvements in the Area Under the ROC curve of 2%-8% compared to state-of-the-art deflation methods. All in all, our approach solves sparse PCA problems with multiple components to certifiable (near) optimality in a practically tractable fashion.

Sparse Plus Low Rank Matrix Decomposition: A Discrete Optimization Approach

We study the Sparse Plus Low Rank decomposition problem (SLR), which is the problem of decomposing a corrupted data matrix $\mathbf{D}$ into a sparse matrix $\mathbf{Y}$ containing the perturbations plus a low rank matrix $\mathbf{X}$. SLR is a fundamental problem in Operations Research and Machine Learning arising in many applications such as data compression, latent semantic indexing, collaborative filtering and medical imaging. We introduce a novel formulation for SLR that directly models the underlying discreteness of the problem. For this formulation, we develop an alternating minimization heuristic to compute high quality solutions and a novel semidefinite relaxation that provides meaningful bounds for the solutions returned by our heuristic. We further develop a custom branch and bound routine that leverages our heuristic and convex relaxation that solves small instances of SLR to certifiable near-optimality. Our heuristic can scale to $n=10000$ in hours, our relaxation can scale to $n=200$ in hours, and our branch and bound algorithm can scale to $n=25$ in minutes. Our numerical results demonstrate that our approach outperforms existing state-of-the-art approaches in terms of the MSE of the low rank matrix and that of the sparse matrix.

A new perspective on low-rank optimization

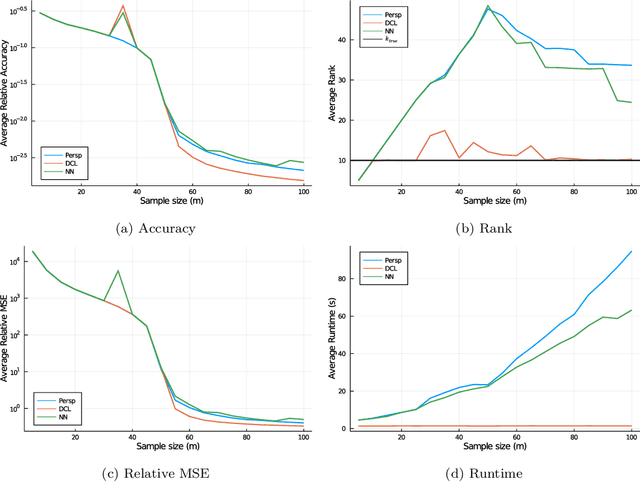
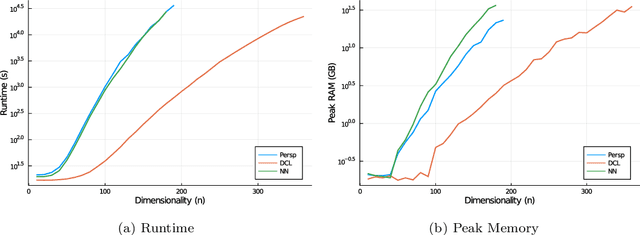
A key question in many low-rank problems throughout optimization, machine learning, and statistics is to characterize the convex hulls of simple low-rank sets and judiciously apply these convex hulls to obtain strong yet computationally tractable convex relaxations. We invoke the matrix perspective function - the matrix analog of the perspective function-and characterize explicitly the convex hull of epigraphs of convex quadratic, matrix exponential, and matrix power functions under low-rank constraints. Further, we exploit these characterizations to develop strong relaxations for a variety of low-rank problems including reduced rank regression, non-negative matrix factorization, and factor analysis. We establish that these relaxations can be modeled via semidefinite and matrix power cone constraints, and thus optimized over tractably. The proposed approach parallels and generalizes the perspective reformulation technique in mixed-integer optimization, and leads to new relaxations for a broad class of problems.

Mixed-Projection Conic Optimization: A New Paradigm for Modeling Rank Constraints

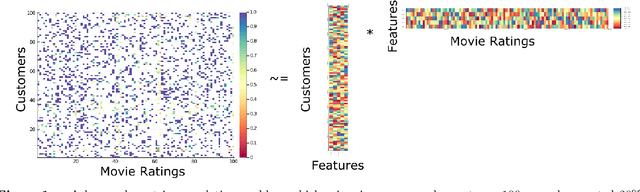
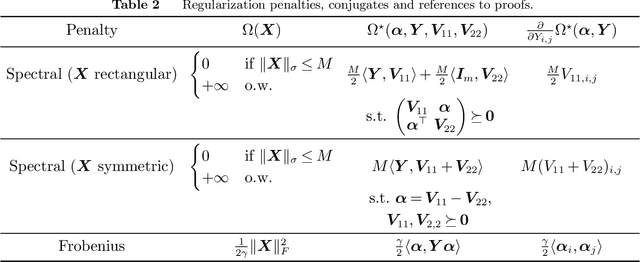
We propose a framework for modeling and solving low-rank optimization problems to certifiable optimality. We introduce symmetric projection matrices that satisfy $Y^2=Y$, the matrix analog of binary variables that satisfy $z^2=z$, to model rank constraints. By leveraging regularization and strong duality, we prove that this modeling paradigm yields tractable convex optimization problems over the non-convex set of orthogonal projection matrices. Furthermore, we design outer-approximation algorithms to solve low-rank problems to certifiable optimality, compute lower bounds via their semidefinite relaxations, and provide near optimal solutions through rounding and local search techniques. We implement these numerical ingredients and, for the first time, solve low-rank optimization problems to certifiable optimality. Our algorithms also supply certifiably near-optimal solutions for larger problem sizes and outperform existing heuristics, by deriving an alternative to the popular nuclear norm relaxation which generalizes the perspective relaxation from vectors to matrices. All in all, our framework, which we name Mixed-Projection Conic Optimization, solves low-rank problems to certifiable optimality in a tractable and unified fashion.

Solving Large-Scale Sparse PCA to Certifiable Optimality

Sparse principal component analysis (PCA) is a popular dimensionality reduction technique for obtaining principal components which are linear combinations of a small subset of the original features. Existing approaches cannot supply certifiably optimal principal components with more than $p=100s$ covariates. By reformulating sparse PCA as a convex mixed-integer semidefinite optimization problem, we design a cutting-plane method which solves the problem to certifiable optimality at the scale of selecting k=10s covariates from p=300 variables, and provides small bound gaps at a larger scale. We also propose two convex relaxations and randomized rounding schemes that provide certifiably near-exact solutions within minutes for p=100s or hours for p=1,000s. Using real-world financial and medical datasets, we illustrate our approach's ability to derive interpretable principal components tractably at scale.

On Polyhedral and Second-Order-Cone Decompositions of Semidefinite Optimization Problems

We study a cutting-plane method for semidefinite optimization problems (SDOs), and supply a proof of the method's convergence, under a boundedness assumption. By relating the method's rate of convergence to an initial outer approximation's diameter, we argue that the method performs well when initialized with a second-order-cone approximation, instead of a linear approximation. We invoke the method to provide bound gaps of 0.5-6.5% for sparse PCA problems with $1000$s of covariates, and solve nuclear norm problems over 500x500 matrices.

A unified approach to mixed-integer optimization: Nonlinear formulations and scalable algorithms

We propose a unified framework to address a family of classical mixed-integer optimization problems, including network design, facility location, unit commitment, sparse portfolio selection, binary quadratic optimization and sparse learning problems. These problems exhibit logical relationships between continuous and discrete variables, which are usually reformulated linearly using a big-M formulation. In this work, we challenge this longstanding modeling practice and express the logical constraints in a non-linear way. By imposing a regularization condition, we reformulate these problems as convex binary optimization problems, which are solvable using an outer-approximation procedure. In numerical experiments, we establish that a general-purpose numerical strategy, which combines cutting-plane, first-order and local search methods, solves these problems faster and at a larger scale than state-of-the-art mixed-integer linear or second-order cone methods. Our approach successfully solves network design problems with 100s of nodes and provides solutions up to 40\% better than the state-of-the-art; sparse portfolio selection problems with up to 3,200 securities compared with 400 securities for previous attempts; and sparse regression problems with up to 100,000 covariates.