AI Hilbert: From Data and Background Knowledge to Automated Scientific Discovery

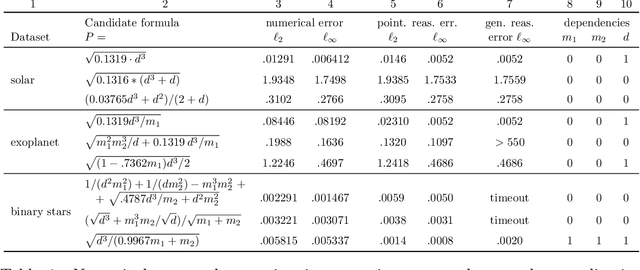
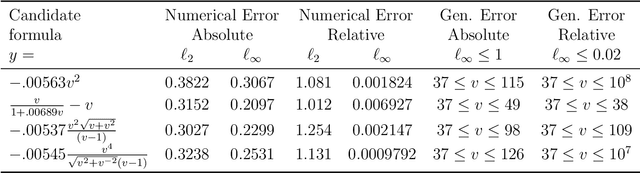
The discovery of scientific formulae that parsimoniously explain natural phenomena and align with existing background theory is a key goal in science. Historically, scientists have derived natural laws by manipulating equations based on existing knowledge, forming new equations, and verifying them experimentally. In recent years, data-driven scientific discovery has emerged as a viable competitor in settings with large amounts of experimental data. Unfortunately, data-driven methods often fail to discover valid laws when data is noisy or scarce. Accordingly, recent works combine regression and reasoning to eliminate formulae inconsistent with background theory. However, the problem of searching over the space of formulae consistent with background theory to find one that fits the data best is not well solved. We propose a solution to this problem when all axioms and scientific laws are expressible via polynomial equalities and inequalities and argue that our approach is widely applicable. We further model notions of minimal complexity using binary variables and logical constraints, solve polynomial optimization problems via mixed-integer linear or semidefinite optimization, and automatically prove the validity of our scientific discoveries via Positivestellensatz certificates. Remarkably, the optimization techniques leveraged in this paper allow our approach to run in polynomial time with fully correct background theory, or non-deterministic polynomial (NP) time with partially correct background theory. We experimentally demonstrate that some famous scientific laws, including Kepler's Third Law of Planetary Motion, the Hagen-Poiseuille Equation, and the Radiated Gravitational Wave Power equation, can be automatically derived from sets of partially correct background axioms.

Integration of Data and Theory for Accelerated Derivable Symbolic Discovery

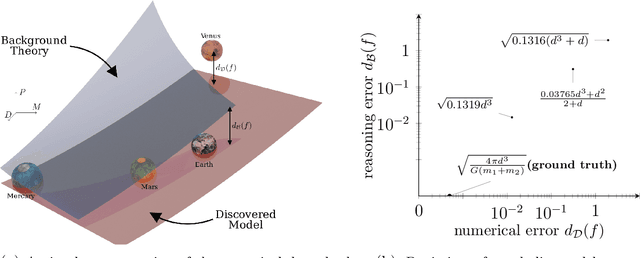
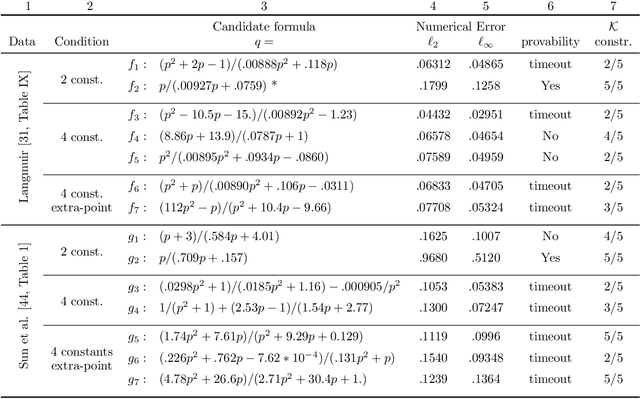
Scientists have long aimed to discover meaningful equations which accurately describe data. Machine learning algorithms automate construction of accurate data-driven models, but ensuring that these are consistent with existing knowledge is a challenge. We developed a methodology combining automated theorem proving with symbolic regression, enabling principled derivations of laws of nature. We demonstrate this for Kepler's third law, Einstein's relativistic time dilation, and Langmuir's theory of adsorption, in each case, automatically connecting experimental data with background theory. The combination of logical reasoning with machine learning provides generalizable insights into key aspects of the natural phenomena.

Piecewise-Linear Motion Planning amidst Static, Moving, or Morphing Obstacles

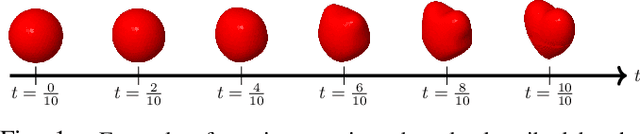
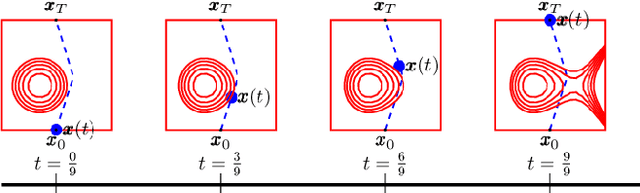
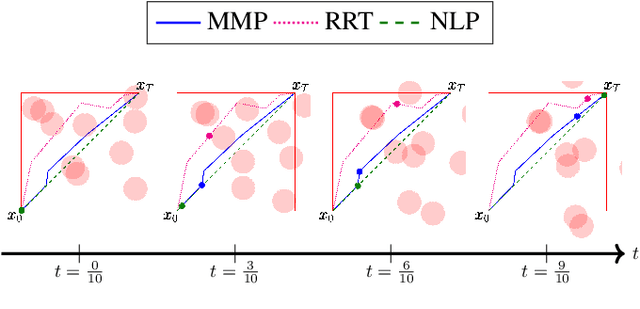
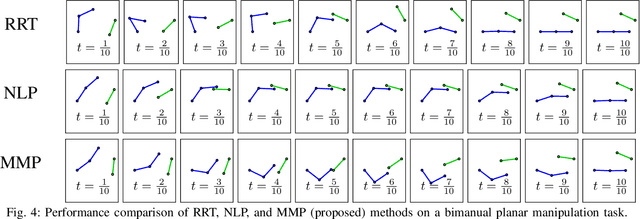
We propose a novel method for planning shortest length piecewise-linear motions through complex environments punctured with static, moving, or even morphing obstacles. Using a moment optimization approach, we formulate a hierarchy of semidefinite programs that yield increasingly refined lower bounds converging monotonically to the optimal path length. For computational tractability, our global moment optimization approach motivates an iterative motion planner that outperforms competing sampling-based and nonlinear optimization baselines. Our method natively handles continuous time constraints without any need for time discretization, and has the potential to scale better with dimensions compared to popular sampling-based methods.

Learning Dynamical Systems with Side Information

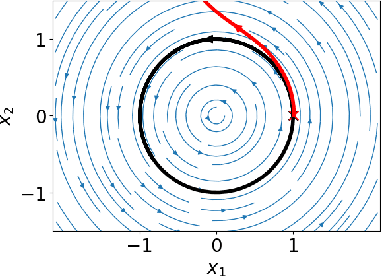
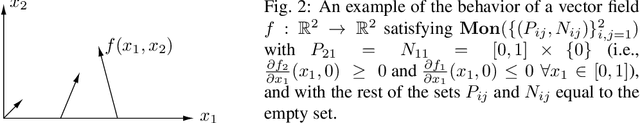
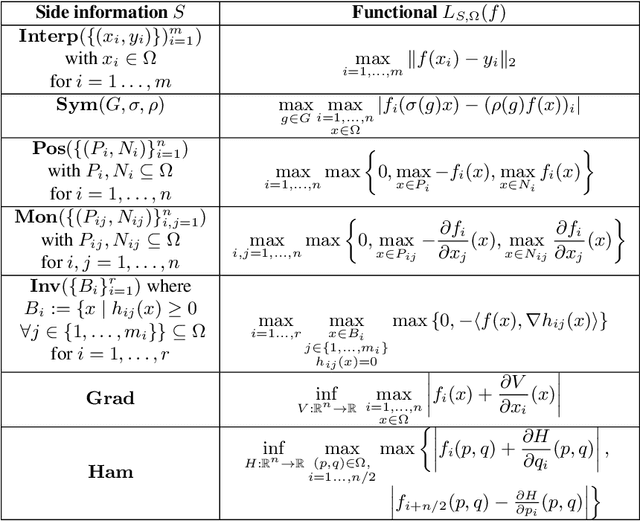
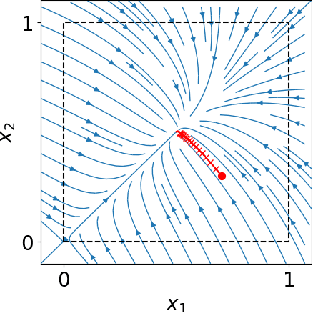
We present a mathematical and computational framework for the problem of learning a dynamical system from noisy observations of a few trajectories and subject to side information. Side information is any knowledge we might have about the dynamical system we would like to learn besides trajectory data. It is typically inferred from domain-specific knowledge or basic principles of a scientific discipline. We are interested in explicitly integrating side information into the learning process in order to compensate for scarcity of trajectory observations. We identify six types of side information that arise naturally in many applications and lead to convex constraints in the learning problem. First, we show that when our model for the unknown dynamical system is parameterized as a polynomial, one can impose our side information constraints computationally via semidefinite programming. We then demonstrate the added value of side information for learning the dynamics of basic models in physics and cell biology, as well as for learning and controlling the dynamics of a model in epidemiology. Finally, we study how well polynomial dynamical systems can approximate continuously-differentiable ones while satisfying side information (either exactly or approximately). Our overall learning methodology combines ideas from convex optimization, real algebra, dynamical systems, and functional approximation theory, and can potentially lead to new synergies between these areas.

Teleoperator Imitation with Continuous-time Safety

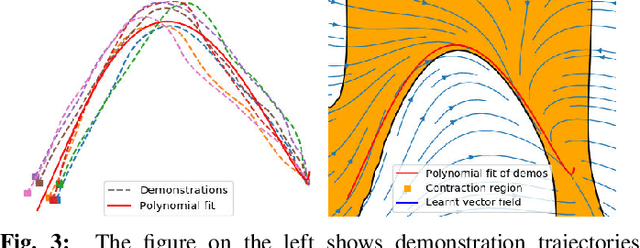
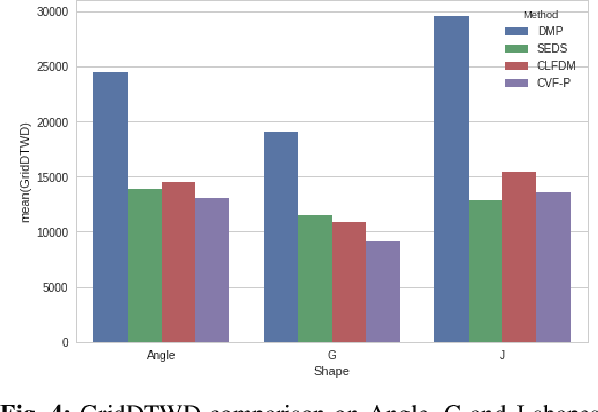
Learning to effectively imitate human teleoperators, with generalization to unseen and dynamic environments, is a promising path to greater autonomy enabling robots to steadily acquire complex skills from supervision. We propose a new motion learning technique rooted in contraction theory and sum-of-squares programming for estimating a control law in the form of a polynomial vector field from a given set of demonstrations. Notably, this vector field is provably optimal for the problem of minimizing imitation loss while providing continuous-time guarantees on the induced imitation behavior. Our method generalizes to new initial and goal poses of the robot and can adapt in real-time to dynamic obstacles during execution, with convergence to teleoperator behavior within a well-defined safety tube. We present an application of our framework for pick-and-place tasks in the presence of moving obstacles on a 7-DOF KUKA IIWA arm. The method compares favorably to other learning-from-demonstration approaches on benchmark handwriting imitation tasks.