Integration of Data and Theory for Accelerated Derivable Symbolic Discovery

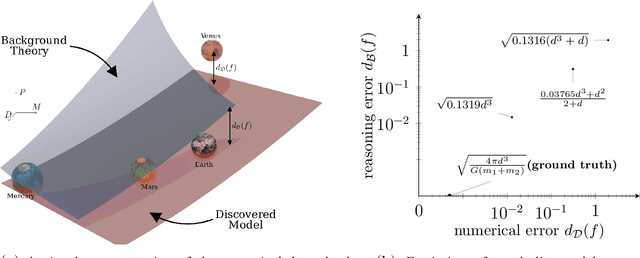
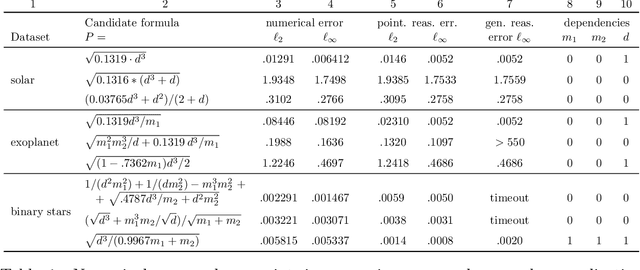
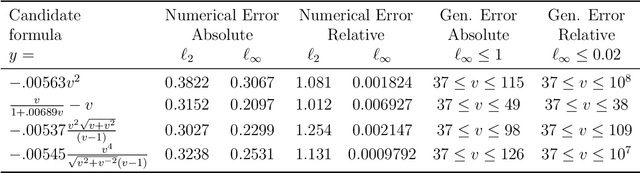
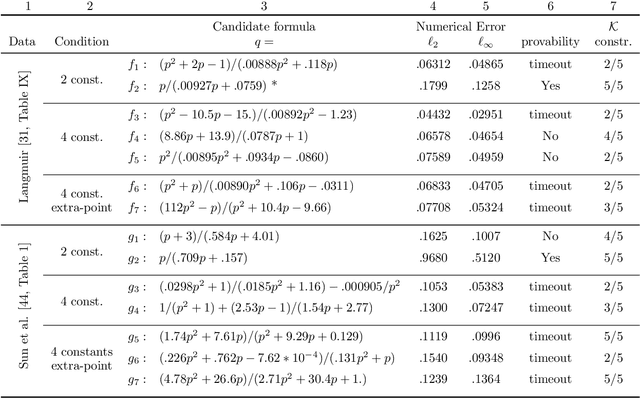
Scientists have long aimed to discover meaningful equations which accurately describe data. Machine learning algorithms automate construction of accurate data-driven models, but ensuring that these are consistent with existing knowledge is a challenge. We developed a methodology combining automated theorem proving with symbolic regression, enabling principled derivations of laws of nature. We demonstrate this for Kepler's third law, Einstein's relativistic time dilation, and Langmuir's theory of adsorption, in each case, automatically connecting experimental data with background theory. The combination of logical reasoning with machine learning provides generalizable insights into key aspects of the natural phenomena.

Symbolic Regression using Mixed-Integer Nonlinear Optimization

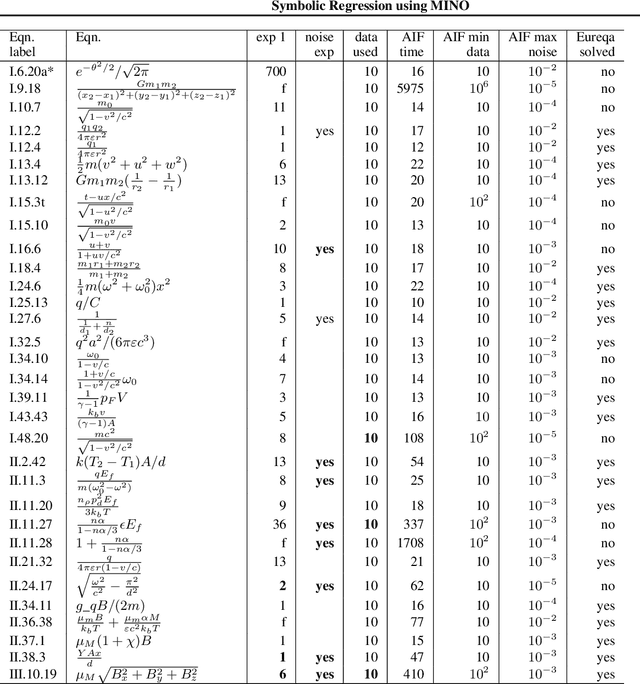
The Symbolic Regression (SR) problem, where the goal is to find a regression function that does not have a pre-specified form but is any function that can be composed of a list of operators, is a hard problem in machine learning, both theoretically and computationally. Genetic programming based methods, that heuristically search over a very large space of functions, are the most commonly used methods to tackle SR problems. An alternative mathematical programming approach, proposed in the last decade, is to express the optimal symbolic expression as the solution of a system of nonlinear equations over continuous and discrete variables that minimizes a certain objective, and to solve this system via a global solver for mixed-integer nonlinear programming problems. Algorithms based on the latter approach are often very slow. We propose a hybrid algorithm that combines mixed-integer nonlinear optimization with explicit enumeration and incorporates constraints from dimensional analysis. We show that our algorithm is competitive, for some synthetic data sets, with a state-of-the-art SR software and a recent physics-inspired method called AI Feynman.