Joao Goncalves
Obtaining Explainable Classification Models using Distributionally Robust Optimization
Nov 03, 2023



Abstract:Model explainability is crucial for human users to be able to interpret how a proposed classifier assigns labels to data based on its feature values. We study generalized linear models constructed using sets of feature value rules, which can capture nonlinear dependencies and interactions. An inherent trade-off exists between rule set sparsity and its prediction accuracy. It is computationally expensive to find the right choice of sparsity -- e.g., via cross-validation -- with existing methods. We propose a new formulation to learn an ensemble of rule sets that simultaneously addresses these competing factors. Good generalization is ensured while keeping computational costs low by utilizing distributionally robust optimization. The formulation utilizes column generation to efficiently search the space of rule sets and constructs a sparse ensemble of rule sets, in contrast with techniques like random forests or boosting and their variants. We present theoretical results that motivate and justify the use of our distributionally robust formulation. Extensive numerical experiments establish that our method improves over competing methods -- on a large set of publicly available binary classification problem instances -- with respect to one or more of the following metrics: generalization quality, computational cost, and explainability.
Bayesian Experimental Design for Symbolic Discovery
Nov 29, 2022Abstract:This study concerns the formulation and application of Bayesian optimal experimental design to symbolic discovery, which is the inference from observational data of predictive models taking general functional forms. We apply constrained first-order methods to optimize an appropriate selection criterion, using Hamiltonian Monte Carlo to sample from the prior. A step for computing the predictive distribution, involving convolution, is computed via either numerical integration, or via fast transform methods.
LPRules: Rule Induction in Knowledge Graphs Using Linear Programming
Oct 15, 2021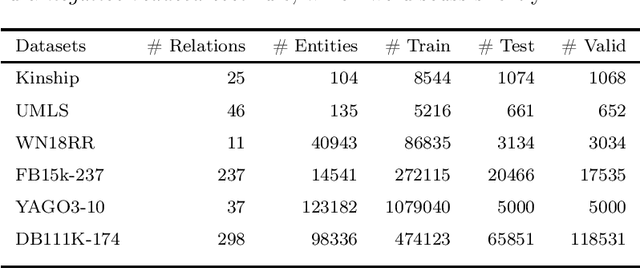
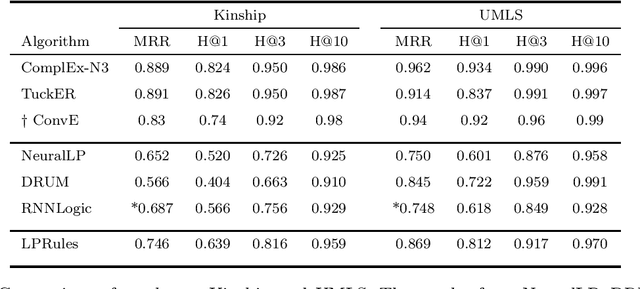
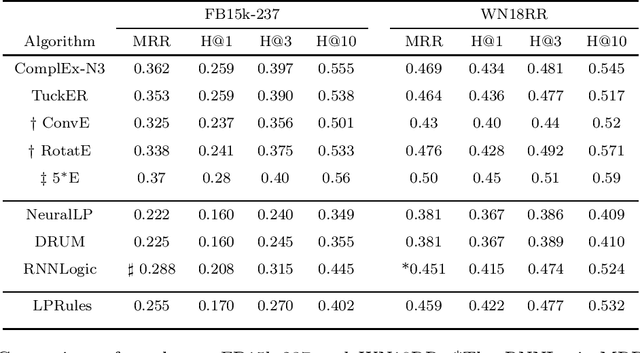
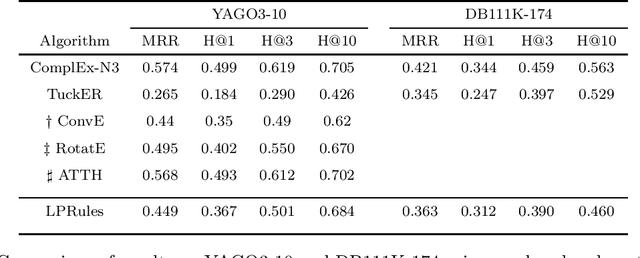
Abstract:Knowledge graph (KG) completion is a well-studied problem in AI. Rule-based methods and embedding-based methods form two of the solution techniques. Rule-based methods learn first-order logic rules that capture existing facts in an input graph and then use these rules for reasoning about missing facts. A major drawback of such methods is the lack of scalability to large datasets. In this paper, we present a simple linear programming (LP) model to choose rules from a list of candidate rules and assign weights to them. For smaller KGs, we use simple heuristics to create the candidate list. For larger KGs, we start with a small initial candidate list, and then use standard column generation ideas to add more rules in order to improve the LP model objective value. To foster interpretability and generalizability, we limit the complexity of the set of chosen rules via explicit constraints, and tune the complexity hyperparameter for individual datasets. We show that our method can obtain state-of-the-art results for three out of four widely used KG datasets, while taking significantly less computing time than other popular rule learners including some based on neuro-symbolic methods. The improved scalability of our method allows us to tackle large datasets such as YAGO3-10.
Integration of Data and Theory for Accelerated Derivable Symbolic Discovery
Sep 03, 2021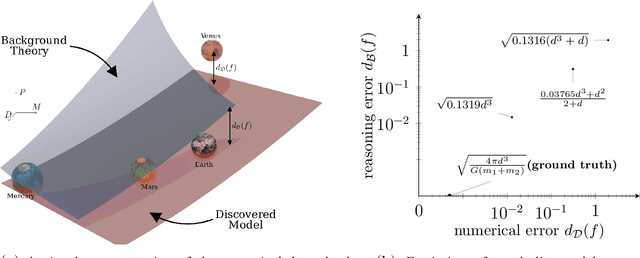
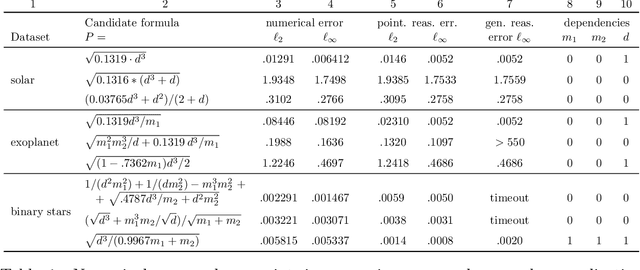
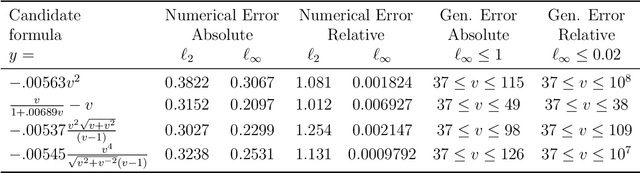
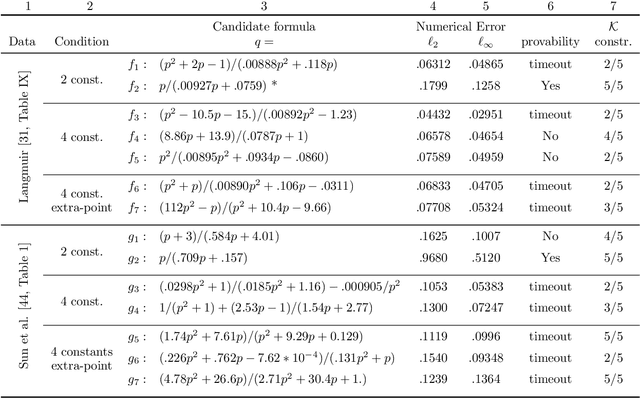
Abstract:Scientists have long aimed to discover meaningful equations which accurately describe data. Machine learning algorithms automate construction of accurate data-driven models, but ensuring that these are consistent with existing knowledge is a challenge. We developed a methodology combining automated theorem proving with symbolic regression, enabling principled derivations of laws of nature. We demonstrate this for Kepler's third law, Einstein's relativistic time dilation, and Langmuir's theory of adsorption, in each case, automatically connecting experimental data with background theory. The combination of logical reasoning with machine learning provides generalizable insights into key aspects of the natural phenomena.
Symbolic Regression using Mixed-Integer Nonlinear Optimization
Jun 11, 2020
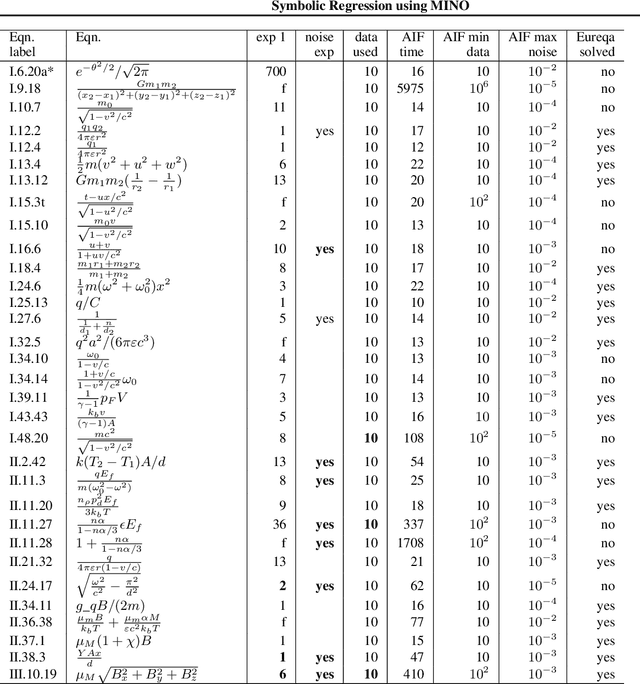
Abstract:The Symbolic Regression (SR) problem, where the goal is to find a regression function that does not have a pre-specified form but is any function that can be composed of a list of operators, is a hard problem in machine learning, both theoretically and computationally. Genetic programming based methods, that heuristically search over a very large space of functions, are the most commonly used methods to tackle SR problems. An alternative mathematical programming approach, proposed in the last decade, is to express the optimal symbolic expression as the solution of a system of nonlinear equations over continuous and discrete variables that minimizes a certain objective, and to solve this system via a global solver for mixed-integer nonlinear programming problems. Algorithms based on the latter approach are often very slow. We propose a hybrid algorithm that combines mixed-integer nonlinear optimization with explicit enumeration and incorporates constraints from dimensional analysis. We show that our algorithm is competitive, for some synthetic data sets, with a state-of-the-art SR software and a recent physics-inspired method called AI Feynman.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge