A General Control-Theoretic Approach for Reinforcement Learning: Theory and Algorithms

We devise a control-theoretic reinforcement learning approach to support direct learning of the optimal policy. We establish theoretical properties of our approach and derive an algorithm based on a specific instance of this approach. Our empirical results demonstrate the significant benefits of our approach.

Obtaining Explainable Classification Models using Distributionally Robust Optimization

Model explainability is crucial for human users to be able to interpret how a proposed classifier assigns labels to data based on its feature values. We study generalized linear models constructed using sets of feature value rules, which can capture nonlinear dependencies and interactions. An inherent trade-off exists between rule set sparsity and its prediction accuracy. It is computationally expensive to find the right choice of sparsity -- e.g., via cross-validation -- with existing methods. We propose a new formulation to learn an ensemble of rule sets that simultaneously addresses these competing factors. Good generalization is ensured while keeping computational costs low by utilizing distributionally robust optimization. The formulation utilizes column generation to efficiently search the space of rule sets and constructs a sparse ensemble of rule sets, in contrast with techniques like random forests or boosting and their variants. We present theoretical results that motivate and justify the use of our distributionally robust formulation. Extensive numerical experiments establish that our method improves over competing methods -- on a large set of publicly available binary classification problem instances -- with respect to one or more of the following metrics: generalization quality, computational cost, and explainability.

Generalization Performance of Transfer Learning: Overparameterized and Underparameterized Regimes

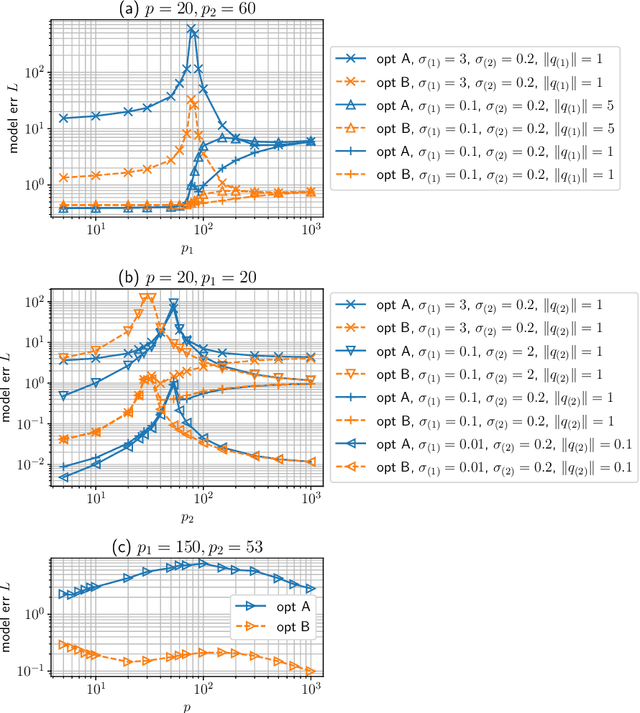
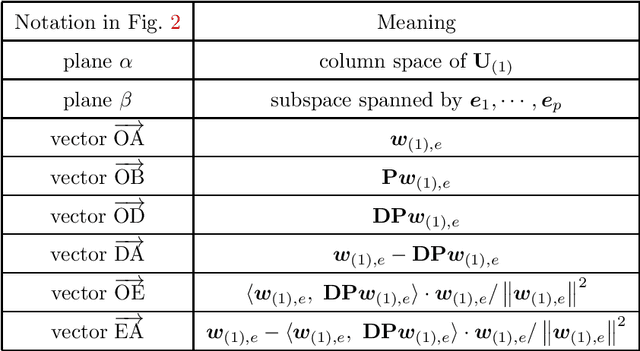
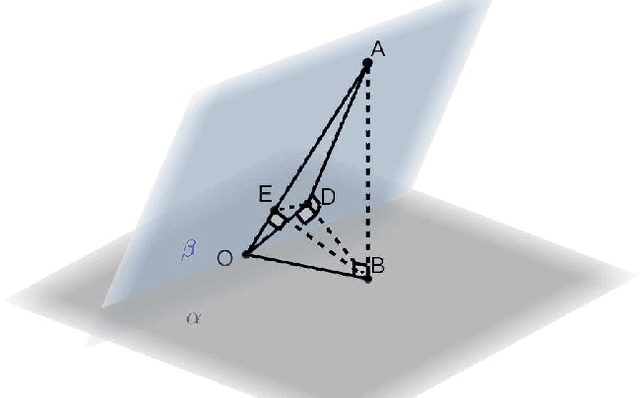
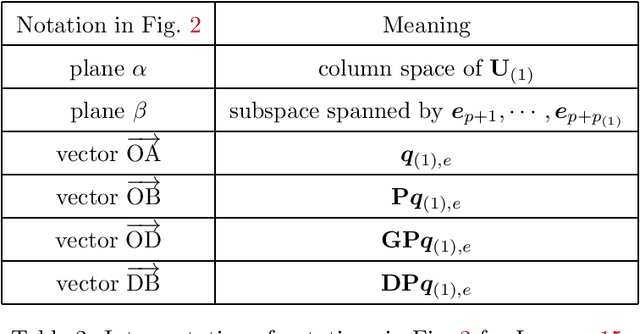
Transfer learning is a useful technique for achieving improved performance and reducing training costs by leveraging the knowledge gained from source tasks and applying it to target tasks. Assessing the effectiveness of transfer learning relies on understanding the similarity between the ground truth of the source and target tasks. In real-world applications, tasks often exhibit partial similarity, where certain aspects are similar while others are different or irrelevant. To investigate the impact of partial similarity on transfer learning performance, we focus on a linear regression model with two distinct sets of features: a common part shared across tasks and a task-specific part. Our study explores various types of transfer learning, encompassing two options for parameter transfer. By establishing a theoretical characterization on the error of the learned model, we compare these transfer learning options, particularly examining how generalization performance changes with the number of features/parameters in both underparameterized and overparameterized regimes. Furthermore, we provide practical guidelines for determining the number of features in the common and task-specific parts for improved generalization performance. For example, when the total number of features in the source task's learning model is fixed, we show that it is more advantageous to allocate a greater number of redundant features to the task-specific part rather than the common part. Moreover, in specific scenarios, particularly those characterized by high noise levels and small true parameters, sacrificing certain true features in the common part in favor of employing more redundant features in the task-specific part can yield notable benefits.

Towards Quantum Advantage on Noisy Quantum Computers

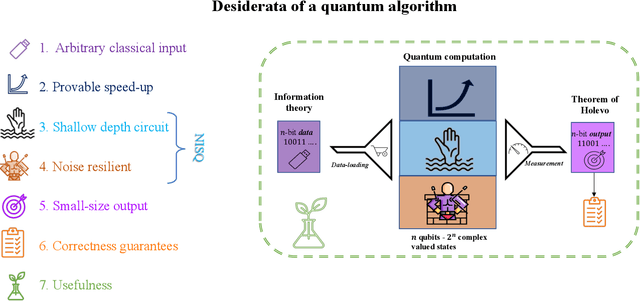
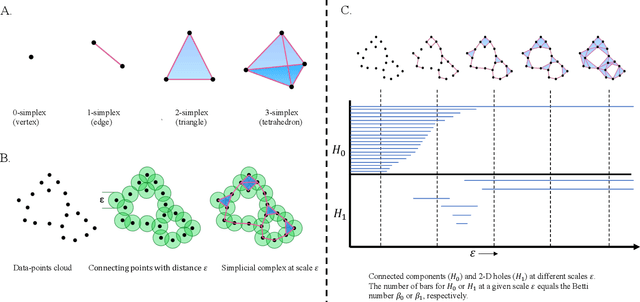
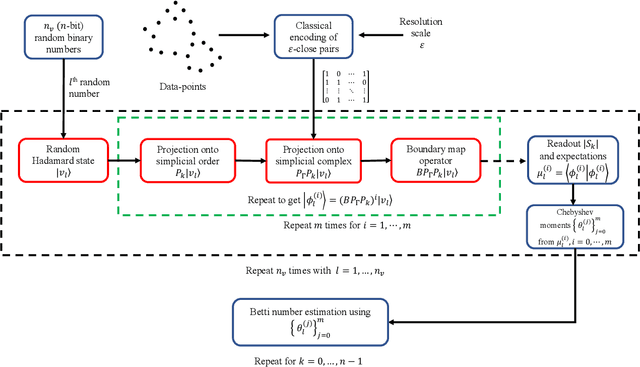
Topological data analysis (TDA) is a powerful technique for extracting complex and valuable shape-related summaries of high-dimensional data. However, the computational demands of classical TDA algorithms are exorbitant, and quickly become impractical for high-order characteristics. Quantum computing promises exponential speedup for certain problems. Yet, many existing quantum algorithms with notable asymptotic speedups require a degree of fault tolerance that is currently unavailable. In this paper, we present NISQ-TDA, the first fully implemented end-to-end quantum machine learning algorithm needing only a linear circuit-depth, that is applicable to non-handcrafted high-dimensional classical data, with potential speedup under stringent conditions. The algorithm neither suffers from the data-loading problem nor does it need to store the input data on the quantum computer explicitly. Our approach includes three key innovations: (a) an efficient realization of the full boundary operator as a sum of Pauli operators; (b) a quantum rejection sampling and projection approach to restrict a uniform superposition to the simplices of the desired order in the complex; and (c) a stochastic rank estimation method to estimate the topological features in the form of approximate Betti numbers. We present theoretical results that establish additive error guarantees for NISQ-TDA, and the circuit and computational time and depth complexities for exponentially scaled output estimates, up to the error tolerance. The algorithm was successfully executed on quantum computing devices, as well as on noisy quantum simulators, applied to small datasets. Preliminary empirical results suggest that the algorithm is robust to noise.

A Class of Geometric Structures in Transfer Learning: Minimax Bounds and Optimality

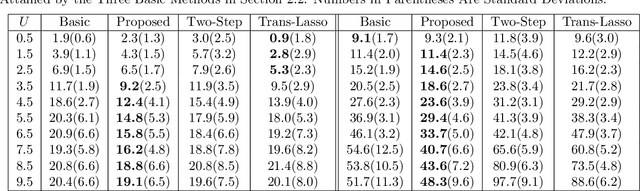
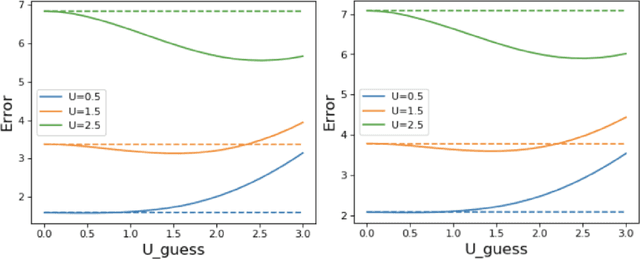
We study the problem of transfer learning, observing that previous efforts to understand its information-theoretic limits do not fully exploit the geometric structure of the source and target domains. In contrast, our study first illustrates the benefits of incorporating a natural geometric structure within a linear regression model, which corresponds to the generalized eigenvalue problem formed by the Gram matrices of both domains. We next establish a finite-sample minimax lower bound, propose a refined model interpolation estimator that enjoys a matching upper bound, and then extend our framework to multiple source domains and generalized linear models. Surprisingly, as long as information is available on the distance between the source and target parameters, negative-transfer does not occur. Simulation studies show that our proposed interpolation estimator outperforms state-of-the-art transfer learning methods in both moderate- and high-dimensional settings.

Quantum Topological Data Analysis with Linear Depth and Exponential Speedup

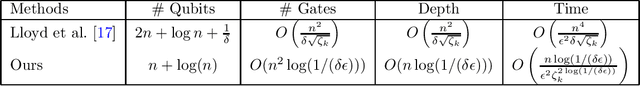
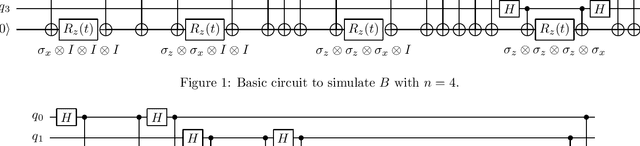
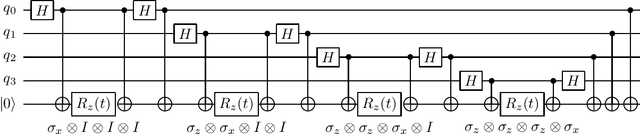
Quantum computing offers the potential of exponential speedups for certain classical computations. Over the last decade, many quantum machine learning (QML) algorithms have been proposed as candidates for such exponential improvements. However, two issues unravel the hope of exponential speedup for some of these QML algorithms: the data-loading problem and, more recently, the stunning dequantization results of Tang et al. A third issue, namely the fault-tolerance requirements of most QML algorithms, has further hindered their practical realization. The quantum topological data analysis (QTDA) algorithm of Lloyd, Garnerone and Zanardi was one of the first QML algorithms that convincingly offered an expected exponential speedup. From the outset, it did not suffer from the data-loading problem. A recent result has also shown that the generalized problem solved by this algorithm is likely classically intractable, and would therefore be immune to any dequantization efforts. However, the QTDA algorithm of Lloyd et~al. has a time complexity of $O(n^4/(\epsilon^2 \delta))$ (where $n$ is the number of data points, $\epsilon$ is the error tolerance, and $\delta$ is the smallest nonzero eigenvalue of the restricted Laplacian) and requires fault-tolerant quantum computing, which has not yet been achieved. In this paper, we completely overhaul the QTDA algorithm to achieve an improved exponential speedup and depth complexity of $O(n\log(1/(\delta\epsilon)))$. Our approach includes three key innovations: (a) an efficient realization of the combinatorial Laplacian as a sum of Pauli operators; (b) a quantum rejection sampling approach to restrict the superposition to the simplices in the complex; and (c) a stochastic rank estimation method to estimate the Betti numbers. We present a theoretical error analysis, and the circuit and computational time and depth complexities for Betti number estimation.

A Control-Model-Based Approach for Reinforcement Learning

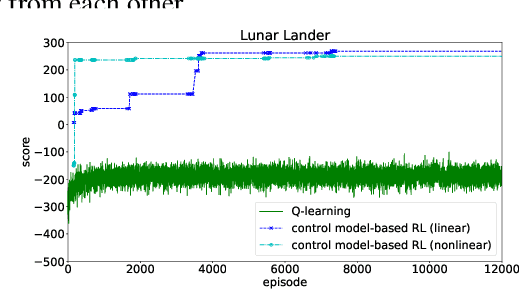
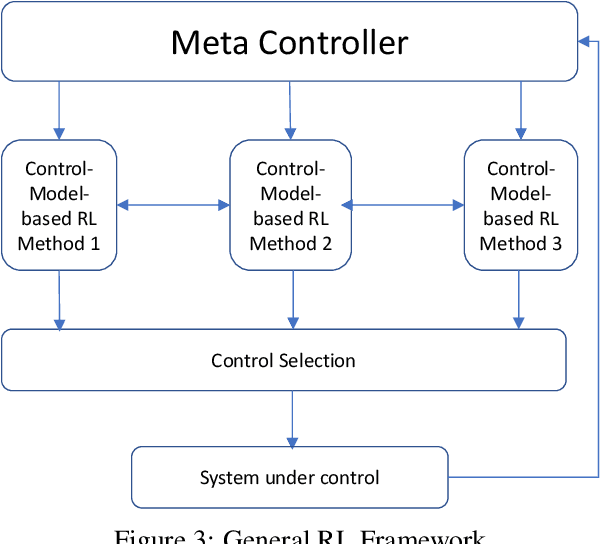
We consider a new form of model-based reinforcement learning methods that directly learns the optimal control parameters, instead of learning the underlying dynamical system. This includes a form of exploration and exploitation in learning and applying the optimal control parameters over time. This also includes a general framework that manages a collection of such control-model-based reinforcement learning methods running in parallel and that selects the best decision from among these parallel methods with the different methods interactively learning together. We derive theoretical results for the optimal control of linear and nonlinear instances of the new control-model-based reinforcement learning methods. Our empirical results demonstrate and quantify the significant benefits of our approach.

PROVEN: Certifying Robustness of Neural Networks with a Probabilistic Approach

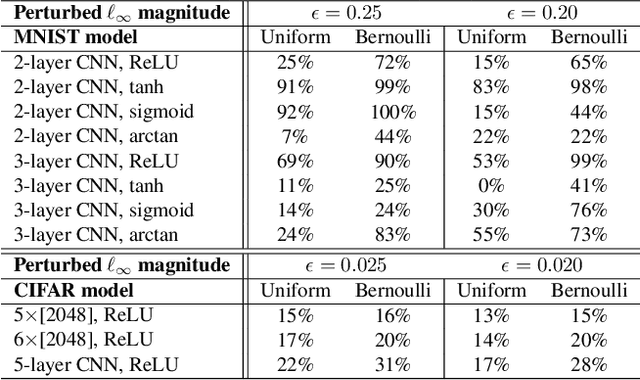
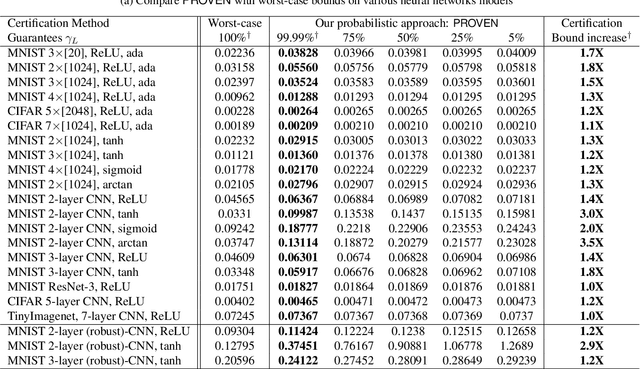
With deep neural networks providing state-of-the-art machine learning models for numerous machine learning tasks, quantifying the robustness of these models has become an important area of research. However, most of the research literature merely focuses on the \textit{worst-case} setting where the input of the neural network is perturbed with noises that are constrained within an $\ell_p$ ball; and several algorithms have been proposed to compute certified lower bounds of minimum adversarial distortion based on such worst-case analysis. In this paper, we address these limitations and extend the approach to a \textit{probabilistic} setting where the additive noises can follow a given distributional characterization. We propose a novel probabilistic framework PROVEN to PRObabilistically VErify Neural networks with statistical guarantees -- i.e., PROVEN certifies the probability that the classifier's top-1 prediction cannot be altered under any constrained $\ell_p$ norm perturbation to a given input. Importantly, we show that it is possible to derive closed-form probabilistic certificates based on current state-of-the-art neural network robustness verification frameworks. Hence, the probabilistic certificates provided by PROVEN come naturally and with almost no overhead when obtaining the worst-case certified lower bounds from existing methods such as Fast-Lin, CROWN and CNN-Cert. Experiments on small and large MNIST and CIFAR neural network models demonstrate our probabilistic approach can achieve up to around $75\%$ improvement in the robustness certification with at least a $99.99\%$ confidence compared with the worst-case robustness certificate delivered by CROWN.

A General Family of Robust Stochastic Operators for Reinforcement Learning

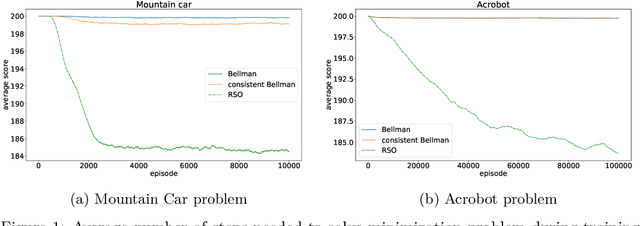
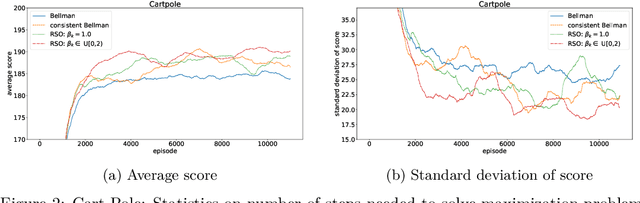
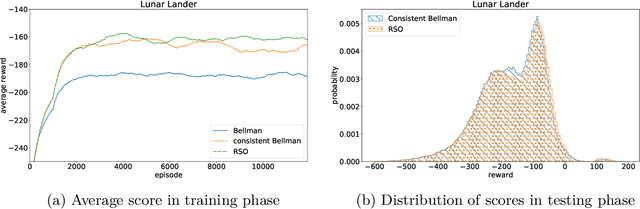
We consider a new family of operators for reinforcement learning with the goal of alleviating the negative effects and becoming more robust to approximation or estimation errors. Various theoretical results are established, which include showing on a sample path basis that our family of operators preserve optimality and increase the action gap. Our empirical results illustrate the strong benefits of our family of operators, significantly outperforming the classical Bellman operator and recently proposed operators.