Monitoring State Transitions in Markovian Systems with Sampling Cost

We consider a node-monitor pair, where the node's state varies with time. The monitor needs to track the node's state at all times; however, there is a fixed cost for each state query. So the monitor may instead predict the state using time-series forecasting methods, including time-series foundation models (TSFMs), and query only when prediction uncertainty is high. Since query decisions influence prediction accuracy, determining when to query is nontrivial. A natural approach is a greedy policy that predicts when the expected prediction loss is below the query cost and queries otherwise. We analyze this policy in a Markovian setting, where the optimal (OPT) strategy is a state-dependent threshold policy minimizing the time-averaged sum of query cost and prediction losses. We show that, in general, the greedy policy is suboptimal and can have an unbounded competitive ratio, but under common conditions such as identically distributed transition probabilities, it performs close to OPT. For the case of unknown transition probabilities, we further propose a projected stochastic gradient descent (PSGD)-based learning variant of the greedy policy, which achieves a favorable predict-query tradeoff with improved computational efficiency compared to OPT.

Provably Efficient RL for Linear MDPs under Instantaneous Safety Constraints in Non-Convex Feature Spaces

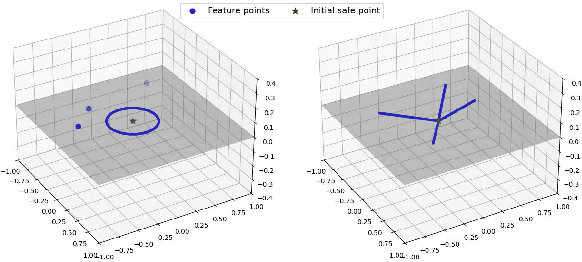
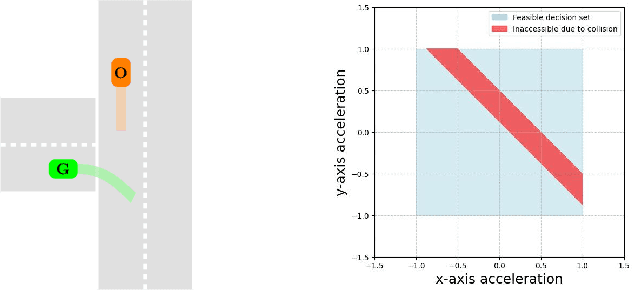
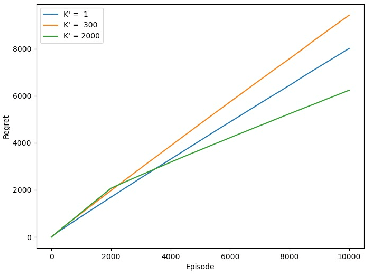
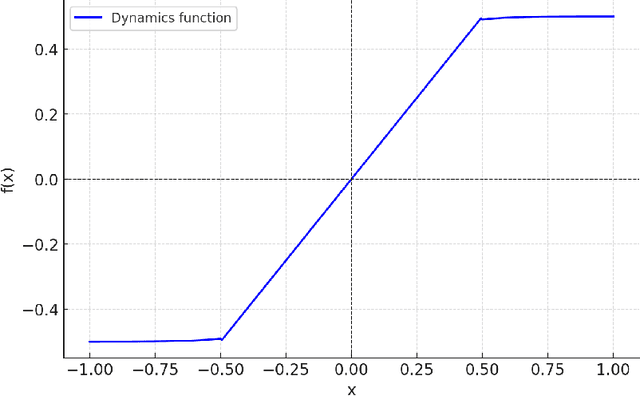
In Reinforcement Learning (RL), tasks with instantaneous hard constraints present significant challenges, particularly when the decision space is non-convex or non-star-convex. This issue is especially relevant in domains like autonomous vehicles and robotics, where constraints such as collision avoidance often take a non-convex form. In this paper, we establish a regret bound of $\tilde{\mathcal{O}}\bigl(\bigl(1 + \tfrac{1}{\tau}\bigr) \sqrt{\log(\tfrac{1}{\tau}) d^3 H^4 K} \bigr)$, applicable to both star-convex and non-star-convex cases, where $d$ is the feature dimension, $H$ the episode length, $K$ the number of episodes, and $\tau$ the safety threshold. Moreover, the violation of safety constraints is zero with high probability throughout the learning process. A key technical challenge in these settings is bounding the covering number of the value-function class, which is essential for achieving value-aware uniform concentration in model-free function approximation. For the star-convex setting, we develop a novel technique called Objective Constraint-Decomposition (OCD) to properly bound the covering number. This result also resolves an error in a previous work on constrained RL. In non-star-convex scenarios, where the covering number can become infinitely large, we propose a two-phase algorithm, Non-Convex Safe Least Squares Value Iteration (NCS-LSVI), which first reduces uncertainty about the safe set by playing a known safe policy. After that, it carefully balances exploration and exploitation to achieve the regret bound. Finally, numerical simulations on an autonomous driving scenario demonstrate the effectiveness of NCS-LSVI.

Provably Efficient Multi-Objective Bandit Algorithms under Preference-Centric Customization

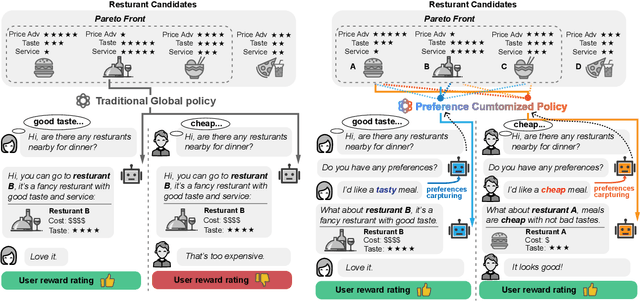
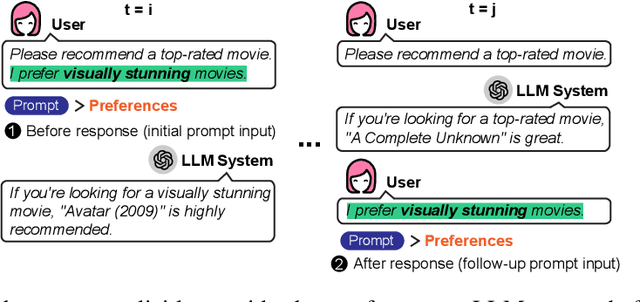
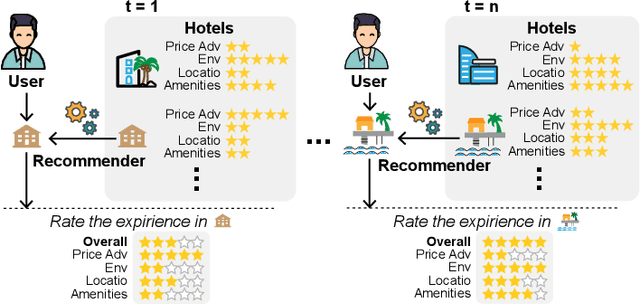
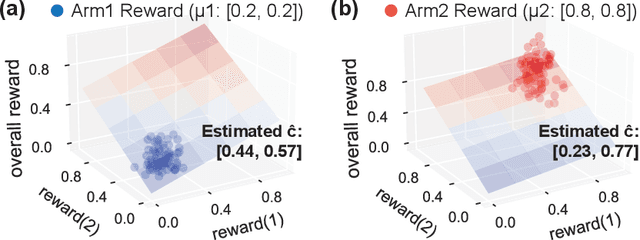
Multi-objective multi-armed bandit (MO-MAB) problems traditionally aim to achieve Pareto optimality. However, real-world scenarios often involve users with varying preferences across objectives, resulting in a Pareto-optimal arm that may score high for one user but perform quite poorly for another. This highlights the need for customized learning, a factor often overlooked in prior research. To address this, we study a preference-aware MO-MAB framework in the presence of explicit user preference. It shifts the focus from achieving Pareto optimality to further optimizing within the Pareto front under preference-centric customization. To our knowledge, this is the first theoretical study of customized MO-MAB optimization with explicit user preferences. Motivated by practical applications, we explore two scenarios: unknown preference and hidden preference, each presenting unique challenges for algorithm design and analysis. At the core of our algorithms are preference estimation and preference-aware optimization mechanisms to adapt to user preferences effectively. We further develop novel analytical techniques to establish near-optimal regret of the proposed algorithms. Strong empirical performance confirm the effectiveness of our approach.

BeST -- A Novel Source Selection Metric for Transfer Learning

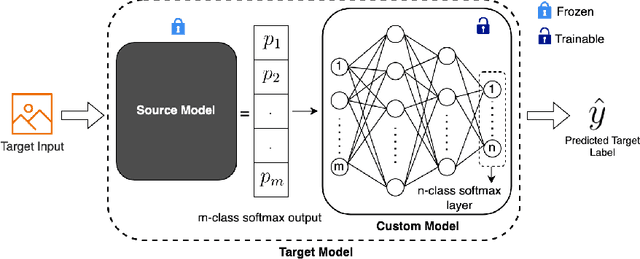
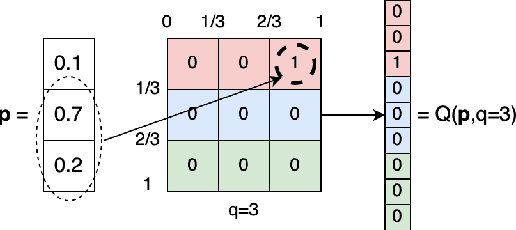
One of the most fundamental, and yet relatively less explored, goals in transfer learning is the efficient means of selecting top candidates from a large number of previously trained models (optimized for various "source" tasks) that would perform the best for a new "target" task with a limited amount of data. In this paper, we undertake this goal by developing a novel task-similarity metric (BeST) and an associated method that consistently performs well in identifying the most transferrable source(s) for a given task. In particular, our design employs an innovative quantization-level optimization procedure in the context of classification tasks that yields a measure of similarity between a source model and the given target data. The procedure uses a concept similar to early stopping (usually implemented to train deep neural networks (DNNs) to ensure generalization) to derive a function that approximates the transfer learning mapping without training. The advantage of our metric is that it can be quickly computed to identify the top candidate(s) for a given target task before a computationally intensive transfer operation (typically using DNNs) can be implemented between the selected source and the target task. As such, our metric can provide significant computational savings for transfer learning from a selection of a large number of possible source models. Through extensive experimental evaluations, we establish that our metric performs well over different datasets and varying numbers of data samples.

Prediction-Assisted Online Distributed Deep Learning Workload Scheduling in GPU Clusters

The recent explosive growth of deep learning (DL) models has necessitated a compelling need for efficient job scheduling for distributed deep learning training with mixed parallelisms (DDLwMP) in GPU clusters. This paper proposes an adaptive shortest-remaining-processing-time-first (A-SRPT) scheduling algorithm, a novel prediction-assisted online scheduling approach designed to mitigate the challenges associated with DL cluster scheduling. By modeling each job as a graph corresponding to heterogeneous Deep Neural Network (DNN) models and their associated distributed training configurations, A-SRPT strategically assigns jobs to the available GPUs, thereby minimizing inter-server communication overhead. Observing that most DDLwMP jobs recur, A-SRPT incorporates a random forest regression model to predict training iterations. Crucially, A-SRPT maps the complex scheduling problem into a single-machine instance, which is addressed optimally by a preemptive "shortest-remaining-processing-time-first" strategy. This optimized solution serves as a guide for actual job scheduling within the GPU clusters, leading to a theoretically provable competitive scheduling efficiency. We conduct extensive real-world testbed and simulation experiments to verify our proposed algorithms.

How to Find the Exact Pareto Front for Multi-Objective MDPs?

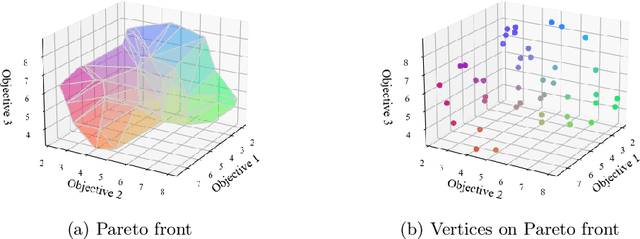
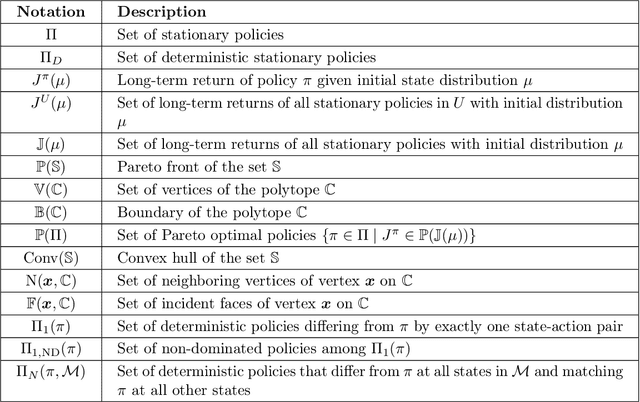
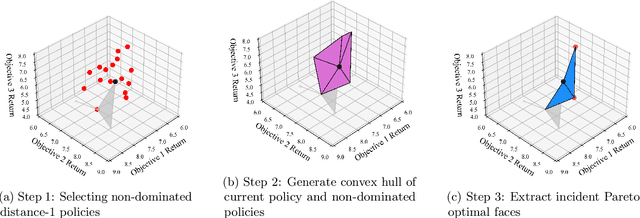
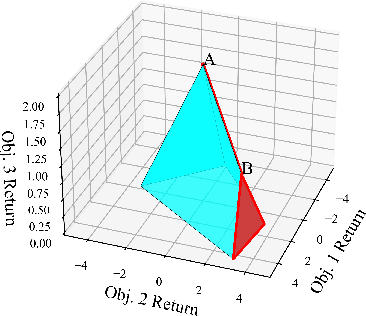
Multi-objective Markov Decision Processes (MDPs) are receiving increasing attention, as real-world decision-making problems often involve conflicting objectives that cannot be addressed by a single-objective MDP. The Pareto front identifies the set of policies that cannot be dominated, providing a foundation for finding optimal solutions that can efficiently adapt to various preferences. However, finding the Pareto front is a highly challenging problem. Most existing methods either (i) rely on traversing the continuous preference space, which is impractical and results in approximations that are difficult to evaluate against the true Pareto front, or (ii) focus solely on deterministic Pareto optimal policies, from which there are no known techniques to characterize the full Pareto front. Moreover, finding the structure of the Pareto front itself remains unclear even in the context of dynamic programming. This work addresses the challenge of efficiently discovering the Pareto front. By investigating the geometric structure of the Pareto front in MO-MDP, we uncover a key property: the Pareto front is on the boundary of a convex polytope whose vertices all correspond to deterministic policies, and neighboring vertices of the Pareto front differ by only one state-action pair of the deterministic policy, almost surely. This insight transforms the global comparison across all policies into a localized search among deterministic policies that differ by only one state-action pair, drastically reducing the complexity of searching for the exact Pareto front. We develop an efficient algorithm that identifies the vertices of the Pareto front by solving a single-objective MDP only once and then traversing the edges of the Pareto front, making it more efficient than existing methods. Our empirical studies demonstrate the effectiveness of our theoretical strategy in discovering the Pareto front.

Theory on Mixture-of-Experts in Continual Learning

Continual learning (CL) has garnered significant attention because of its ability to adapt to new tasks that arrive over time. Catastrophic forgetting (of old tasks) has been identified as a major issue in CL, as the model adapts to new tasks. The Mixture-of-Experts (MoE) model has recently been shown to effectively mitigate catastrophic forgetting in CL, by employing a gating network to sparsify and distribute diverse tasks among multiple experts. However, there is a lack of theoretical analysis of MoE and its impact on the learning performance in CL. This paper provides the first theoretical results to characterize the impact of MoE in CL via the lens of overparameterized linear regression tasks. We establish the benefit of MoE over a single expert by proving that the MoE model can diversify its experts to specialize in different tasks, while its router learns to select the right expert for each task and balance the loads across all experts. Our study further suggests an intriguing fact that the MoE in CL needs to terminate the update of the gating network after sufficient training rounds to attain system convergence, which is not needed in the existing MoE studies that do not consider the continual task arrival. Furthermore, we provide explicit expressions for the expected forgetting and overall generalization error to characterize the benefit of MoE in the learning performance in CL. Interestingly, adding more experts requires additional rounds before convergence, which may not enhance the learning performance. Finally, we conduct experiments on both synthetic and real datasets to extend these insights from linear models to deep neural networks (DNNs), which also shed light on the practical algorithm design for MoE in CL.

Generalization Performance of Transfer Learning: Overparameterized and Underparameterized Regimes

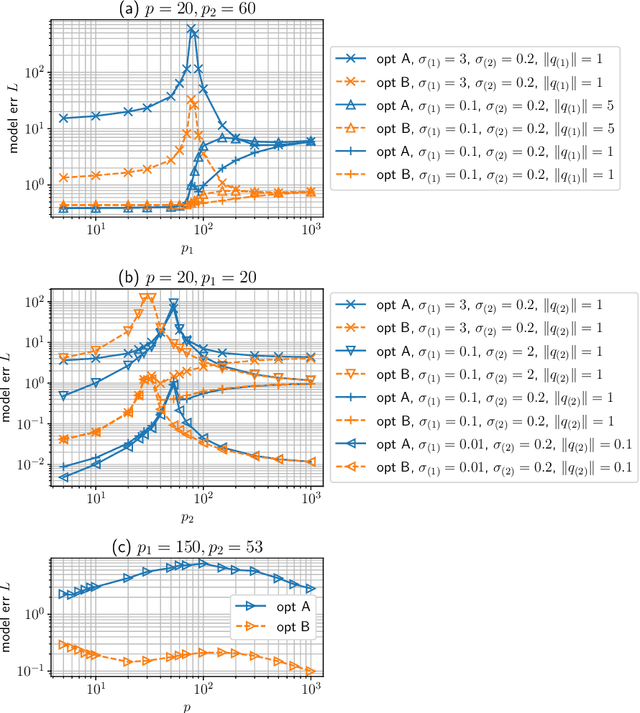
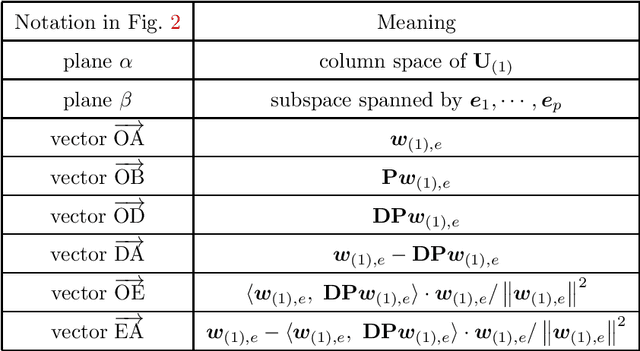
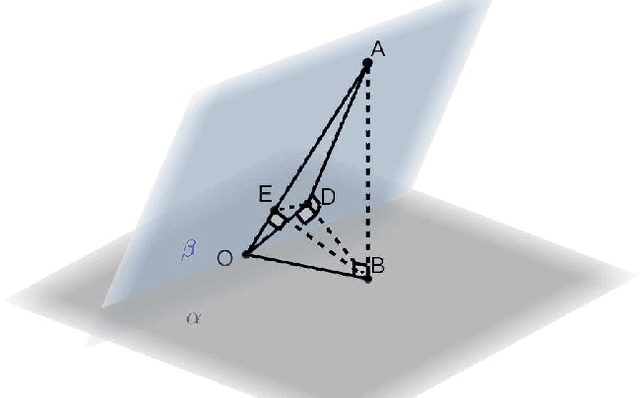
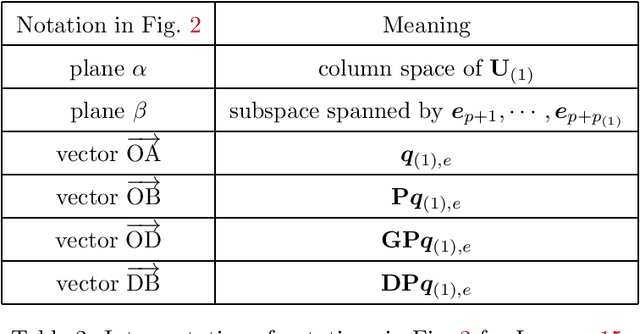
Transfer learning is a useful technique for achieving improved performance and reducing training costs by leveraging the knowledge gained from source tasks and applying it to target tasks. Assessing the effectiveness of transfer learning relies on understanding the similarity between the ground truth of the source and target tasks. In real-world applications, tasks often exhibit partial similarity, where certain aspects are similar while others are different or irrelevant. To investigate the impact of partial similarity on transfer learning performance, we focus on a linear regression model with two distinct sets of features: a common part shared across tasks and a task-specific part. Our study explores various types of transfer learning, encompassing two options for parameter transfer. By establishing a theoretical characterization on the error of the learned model, we compare these transfer learning options, particularly examining how generalization performance changes with the number of features/parameters in both underparameterized and overparameterized regimes. Furthermore, we provide practical guidelines for determining the number of features in the common and task-specific parts for improved generalization performance. For example, when the total number of features in the source task's learning model is fixed, we show that it is more advantageous to allocate a greater number of redundant features to the task-specific part rather than the common part. Moreover, in specific scenarios, particularly those characterized by high noise levels and small true parameters, sacrificing certain true features in the common part in favor of employing more redundant features in the task-specific part can yield notable benefits.

Achieving Fairness in Multi-Agent Markov Decision Processes Using Reinforcement Learning

Fairness plays a crucial role in various multi-agent systems (e.g., communication networks, financial markets, etc.). Many multi-agent dynamical interactions can be cast as Markov Decision Processes (MDPs). While existing research has focused on studying fairness in known environments, the exploration of fairness in such systems for unknown environments remains open. In this paper, we propose a Reinforcement Learning (RL) approach to achieve fairness in multi-agent finite-horizon episodic MDPs. Instead of maximizing the sum of individual agents' value functions, we introduce a fairness function that ensures equitable rewards across agents. Since the classical Bellman's equation does not hold when the sum of individual value functions is not maximized, we cannot use traditional approaches. Instead, in order to explore, we maintain a confidence bound of the unknown environment and then propose an online convex optimization based approach to obtain a policy constrained to this confidence region. We show that such an approach achieves sub-linear regret in terms of the number of episodes. Additionally, we provide a probably approximately correct (PAC) guarantee based on the obtained regret bound. We also propose an offline RL algorithm and bound the optimality gap with respect to the optimal fair solution. To mitigate computational complexity, we introduce a policy-gradient type method for the fair objective. Simulation experiments also demonstrate the efficacy of our approach.

Theoretical Characterization of the Generalization Performance of Overfitted Meta-Learning

Meta-learning has arisen as a successful method for improving training performance by training over many similar tasks, especially with deep neural networks (DNNs). However, the theoretical understanding of when and why overparameterized models such as DNNs can generalize well in meta-learning is still limited. As an initial step towards addressing this challenge, this paper studies the generalization performance of overfitted meta-learning under a linear regression model with Gaussian features. In contrast to a few recent studies along the same line, our framework allows the number of model parameters to be arbitrarily larger than the number of features in the ground truth signal, and hence naturally captures the overparameterized regime in practical deep meta-learning. We show that the overfitted min $\ell_2$-norm solution of model-agnostic meta-learning (MAML) can be beneficial, which is similar to the recent remarkable findings on ``benign overfitting'' and ``double descent'' phenomenon in the classical (single-task) linear regression. However, due to the uniqueness of meta-learning such as task-specific gradient descent inner training and the diversity/fluctuation of the ground-truth signals among training tasks, we find new and interesting properties that do not exist in single-task linear regression. We first provide a high-probability upper bound (under reasonable tightness) on the generalization error, where certain terms decrease when the number of features increases. Our analysis suggests that benign overfitting is more significant and easier to observe when the noise and the diversity/fluctuation of the ground truth of each training task are large. Under this circumstance, we show that the overfitted min $\ell_2$-norm solution can achieve an even lower generalization error than the underparameterized solution.