Probe-then-Commit Multi-Objective Bandits: Theoretical Benefits of Limited Multi-Arm Feedback

We study an online resource-selection problem motivated by multi-radio access selection and mobile edge computing offloading. In each round, an agent chooses among $K$ candidate links/servers (arms) whose performance is a stochastic $d$-dimensional vector (e.g., throughput, latency, energy, reliability). The key interaction is \emph{probe-then-commit (PtC)}: the agent may probe up to $q>1$ candidates via control-plane measurements to observe their vector outcomes, but must execute exactly one candidate in the data plane. This limited multi-arm feedback regime strictly interpolates between classical bandits ($q=1$) and full-information experts ($q=K$), yet existing multi-objective learning theory largely focuses on these extremes. We develop \textsc{PtC-P-UCB}, an optimistic probe-then-commit algorithm whose technical core is frontier-aware probing under uncertainty in a Pareto mode, e.g., it selects the $q$ probes by approximately maximizing a hypervolume-inspired frontier-coverage potential and commits by marginal hypervolume gain to directly expand the attained Pareto region. We prove a dominated-hypervolume frontier error of $\tilde{O} (K_P d/\sqrt{qT})$, where $K_P$ is the Pareto-frontier size and $T$ is the horizon, and scalarized regret $\tilde{O} (L_φd\sqrt{(K/q)T})$, where $φ$ is the scalarizer. These quantify a transparent $1/\sqrt{q}$ acceleration from limited probing. We further extend to \emph{multi-modal probing}: each probe returns $M$ modalities (e.g., CSI, queue, compute telemetry), and uncertainty fusion yields variance-adaptive versions of the above bounds via an effective noise scale.

Bi-Level Online Provisioning and Scheduling with Switching Costs and Cross-Level Constraints

We study a bi-level online provisioning and scheduling problem motivated by network resource allocation, where provisioning decisions are made at a slow time scale while queue-/state-dependent scheduling is performed at a fast time scale. We model this two-time-scale interaction using an upper-level online convex optimization (OCO) problem and a lower-level constrained Markov decision process (CMDP). Existing OCO typically assumes stateless decisions and thus cannot capture MDP network dynamics such as queue evolution. Meanwhile, CMDP algorithms typically assume a fixed constraint threshold, whereas in provisioning-and-scheduling systems, the threshold varies with online budget decisions. To address these gaps, we study bi-level OCO-CMDP learning under switching costs (budget reprovisioning/system reconfiguration) and cross-level constraints that couple budgets to scheduling decisions. Our new algorithm solves this learning problem via several non-trivial developments, including a carefully designed dual feedback that returns the budget multiplier as sensitivity information for the upper-level update and a lower level that solves a budget-adaptive safe exploration problem via an extended occupancy-measure linear program. We establish near-optimal regret and high-probability satisfaction of the cross-level constraints.

Communication-Corruption Coupling and Verification in Cooperative Multi-Objective Bandits

We study cooperative stochastic multi-armed bandits with vector-valued rewards under adversarial corruption and limited verification. In each of $T$ rounds, each of $N$ agents selects an arm, the environment generates a clean reward vector, and an adversary perturbs the observed feedback subject to a global corruption budget $Γ$. Performance is measured by team regret under a coordinate-wise nondecreasing, $L$-Lipschitz scalarization $φ$, covering linear, Chebyshev, and smooth monotone utilities. Our main contribution is a communication-corruption coupling: we show that a fixed environment-side budget $Γ$ can translate into an effective corruption level ranging from $Γ$ to $NΓ$, depending on whether agents share raw samples, sufficient statistics, or only arm recommendations. We formalize this via a protocol-induced multiplicity functional and prove regret bounds parameterized by the resulting effective corruption. As corollaries, raw-sample sharing can suffer an $N$-fold larger additive corruption penalty, whereas summary sharing and recommendation-only sharing preserve an unamplified $O(Γ)$ term and achieve centralized-rate team regret. We further establish information-theoretic limits, including an unavoidable additive $Ω(Γ)$ penalty and a high-corruption regime $Γ=Θ(NT)$ where sublinear regret is impossible without clean information. Finally, we characterize how a global budget $ν$ of verified observations restores learnability. That is, verification is necessary in the high-corruption regime, and sufficient once it crosses the identification threshold, with certified sharing enabling the team's regret to become independent of $Γ$.

Provably Efficient RL for Linear MDPs under Instantaneous Safety Constraints in Non-Convex Feature Spaces

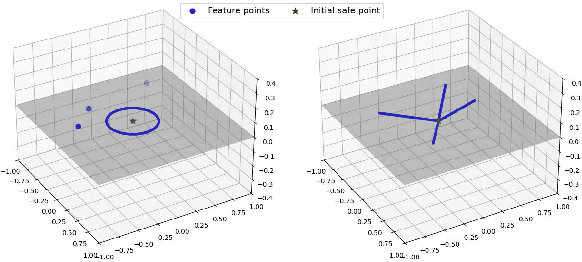
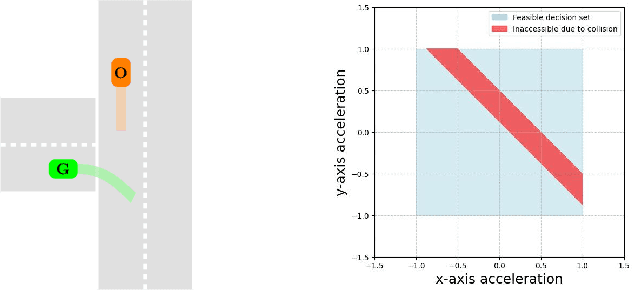
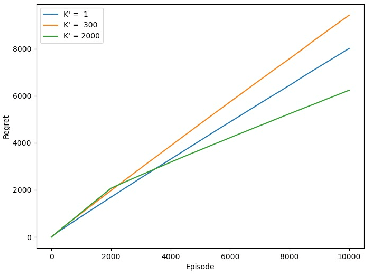
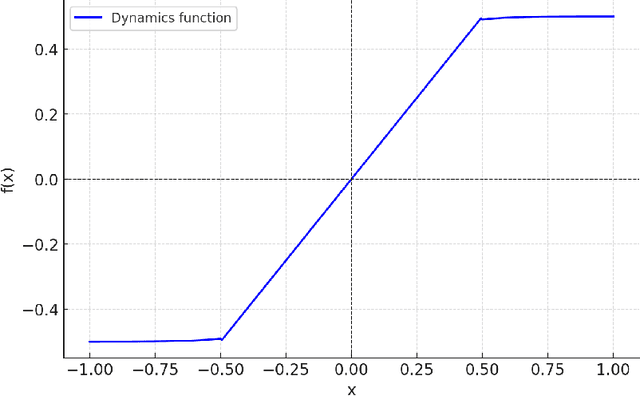
In Reinforcement Learning (RL), tasks with instantaneous hard constraints present significant challenges, particularly when the decision space is non-convex or non-star-convex. This issue is especially relevant in domains like autonomous vehicles and robotics, where constraints such as collision avoidance often take a non-convex form. In this paper, we establish a regret bound of $\tilde{\mathcal{O}}\bigl(\bigl(1 + \tfrac{1}{\tau}\bigr) \sqrt{\log(\tfrac{1}{\tau}) d^3 H^4 K} \bigr)$, applicable to both star-convex and non-star-convex cases, where $d$ is the feature dimension, $H$ the episode length, $K$ the number of episodes, and $\tau$ the safety threshold. Moreover, the violation of safety constraints is zero with high probability throughout the learning process. A key technical challenge in these settings is bounding the covering number of the value-function class, which is essential for achieving value-aware uniform concentration in model-free function approximation. For the star-convex setting, we develop a novel technique called Objective Constraint-Decomposition (OCD) to properly bound the covering number. This result also resolves an error in a previous work on constrained RL. In non-star-convex scenarios, where the covering number can become infinitely large, we propose a two-phase algorithm, Non-Convex Safe Least Squares Value Iteration (NCS-LSVI), which first reduces uncertainty about the safe set by playing a known safe policy. After that, it carefully balances exploration and exploitation to achieve the regret bound. Finally, numerical simulations on an autonomous driving scenario demonstrate the effectiveness of NCS-LSVI.

Provably Efficient Multi-Objective Bandit Algorithms under Preference-Centric Customization

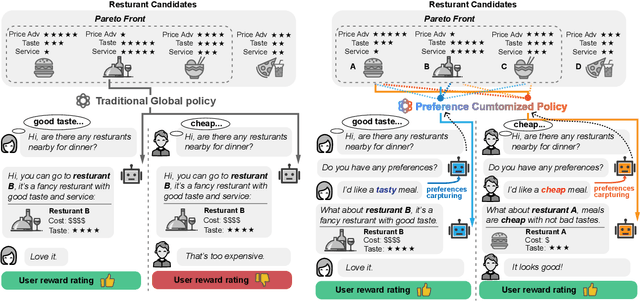
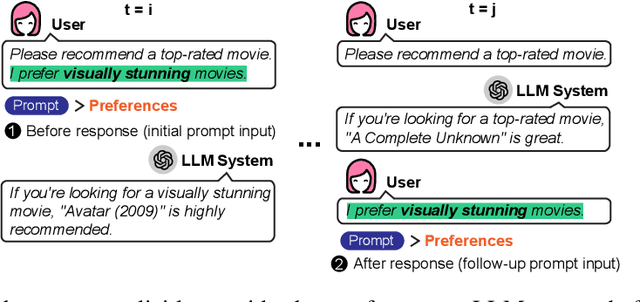
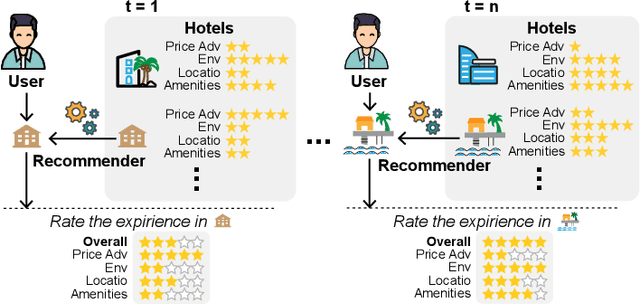
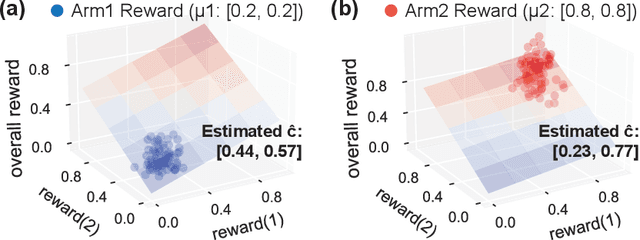
Multi-objective multi-armed bandit (MO-MAB) problems traditionally aim to achieve Pareto optimality. However, real-world scenarios often involve users with varying preferences across objectives, resulting in a Pareto-optimal arm that may score high for one user but perform quite poorly for another. This highlights the need for customized learning, a factor often overlooked in prior research. To address this, we study a preference-aware MO-MAB framework in the presence of explicit user preference. It shifts the focus from achieving Pareto optimality to further optimizing within the Pareto front under preference-centric customization. To our knowledge, this is the first theoretical study of customized MO-MAB optimization with explicit user preferences. Motivated by practical applications, we explore two scenarios: unknown preference and hidden preference, each presenting unique challenges for algorithm design and analysis. At the core of our algorithms are preference estimation and preference-aware optimization mechanisms to adapt to user preferences effectively. We further develop novel analytical techniques to establish near-optimal regret of the proposed algorithms. Strong empirical performance confirm the effectiveness of our approach.

Theoretical Hardness and Tractability of POMDPs in RL with Partial Hindsight State Information

Partially observable Markov decision processes (POMDPs) have been widely applied to capture many real-world applications. However, existing theoretical results have shown that learning in general POMDPs could be intractable, where the main challenge lies in the lack of latent state information. A key fundamental question here is how much hindsight state information (HSI) is sufficient to achieve tractability. In this paper, we establish a lower bound that reveals a surprising hardness result: unless we have full HSI, we need an exponentially scaling sample complexity to obtain an $\epsilon$-optimal policy solution for POMDPs. Nonetheless, from the key insights in our lower-bound construction, we find that there exist important tractable classes of POMDPs even with partial HSI. In particular, for two novel classes of POMDPs with partial HSI, we provide new algorithms that are shown to be near-optimal by establishing new upper and lower bounds.

Self-training with dual uncertainty for semi-supervised medical image segmentation

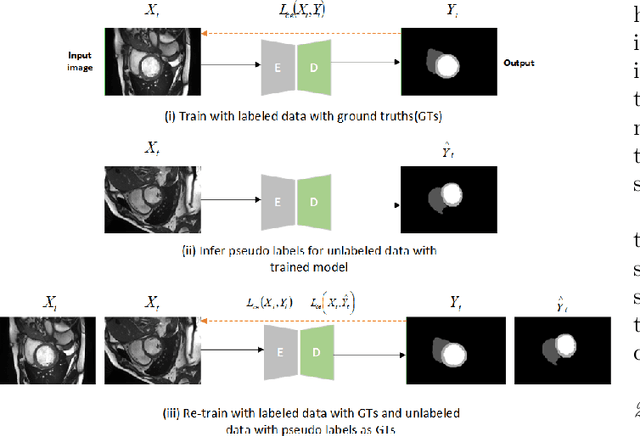
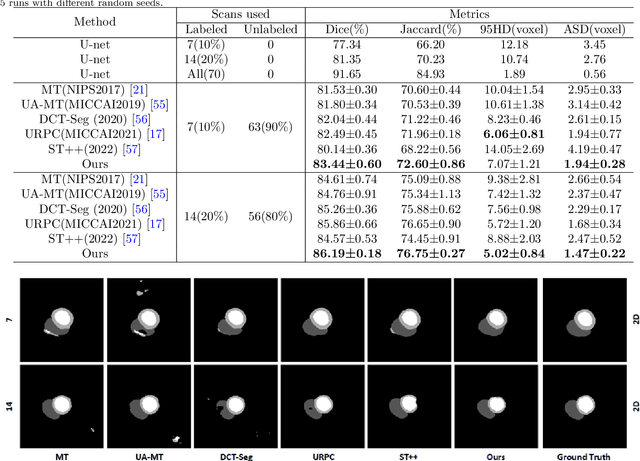
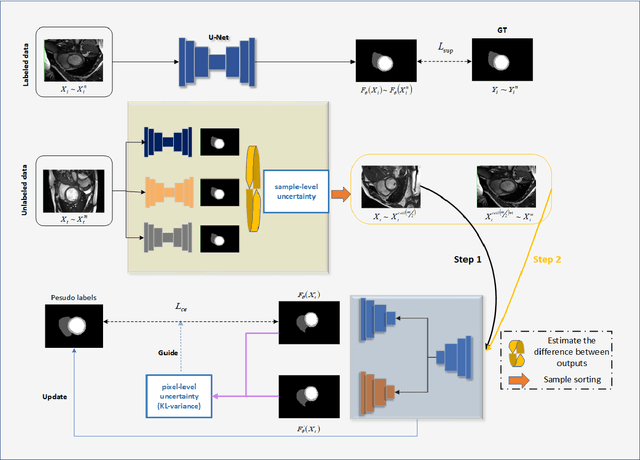
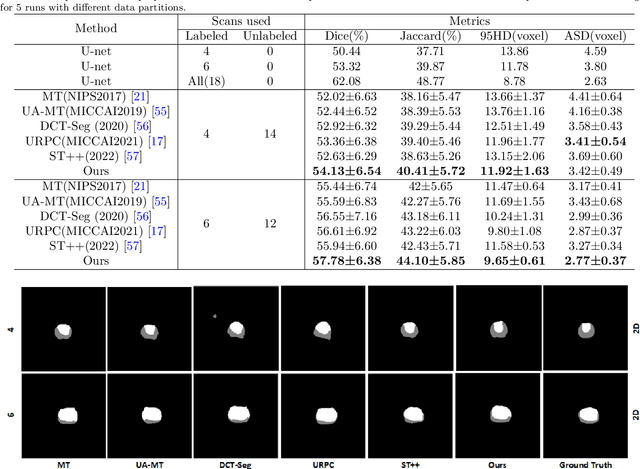
In the field of semi-supervised medical image segmentation, the shortage of labeled data is the fundamental problem. How to effectively learn image features from unlabeled images to improve segmentation accuracy is the main research direction in this field. Traditional self-training methods can partially solve the problem of insufficient labeled data by generating pseudo labels for iterative training. However, noise generated due to the model's uncertainty during training directly affects the segmentation results. Therefore, we added sample-level and pixel-level uncertainty to stabilize the training process based on the self-training framework. Specifically, we saved several moments of the model during pre-training, and used the difference between their predictions on unlabeled samples as the sample-level uncertainty estimate for that sample. Then, we gradually add unlabeled samples from easy to hard during training. At the same time, we added a decoder with different upsampling methods to the segmentation network and used the difference between the outputs of the two decoders as pixel-level uncertainty. In short, we selectively retrained unlabeled samples and assigned pixel-level uncertainty to pseudo labels to optimize the self-training process. We compared the segmentation results of our model with five semi-supervised approaches on the public 2017 ACDC dataset and 2018 Prostate dataset. Our proposed method achieves better segmentation performance on both datasets under the same settings, demonstrating its effectiveness, robustness, and potential transferability to other medical image segmentation tasks. Keywords: Medical image segmentation, semi-supervised learning, self-training, uncertainty estimation

HD-GCN:A Hybrid Diffusion Graph Convolutional Network

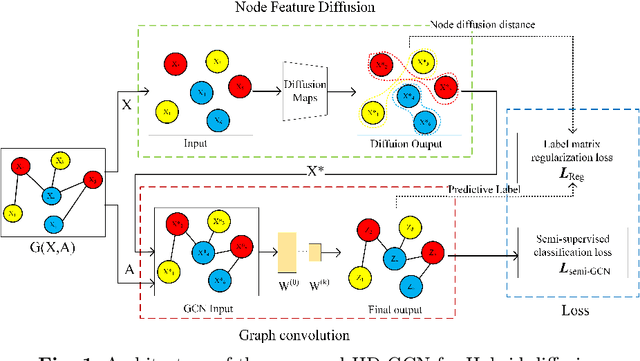
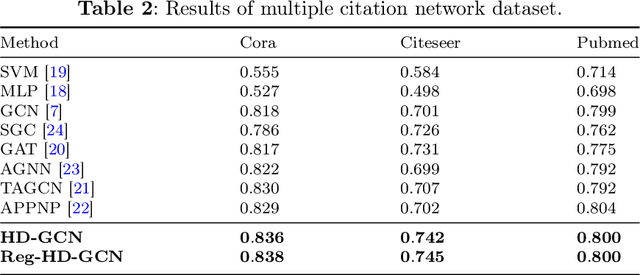
The information diffusion performance of GCN and its variant models is limited by the adjacency matrix, which can lower their performance. Therefore, we introduce a new framework for graph convolutional networks called Hybrid Diffusion-based Graph Convolutional Network (HD-GCN) to address the limitations of information diffusion caused by the adjacency matrix. In the HD-GCN framework, we initially utilize diffusion maps to facilitate the diffusion of information among nodes that are adjacent to each other in the feature space. This allows for the diffusion of information between similar points that may not have an adjacent relationship. Next, we utilize graph convolution to further propagate information among adjacent nodes after the diffusion maps, thereby enabling the spread of information among similar nodes that are adjacent in the graph. Finally, we employ the diffusion distances obtained through the use of diffusion maps to regularize and constrain the predicted labels of training nodes. This regularization method is then applied to the HD-GCN training, resulting in a smoother classification surface. The model proposed in this paper effectively overcomes the limitations of information diffusion imposed only by the adjacency matrix. HD-GCN utilizes hybrid diffusion by combining information diffusion between neighborhood nodes in the feature space and adjacent nodes in the adjacency matrix. This method allows for more comprehensive information propagation among nodes, resulting in improved model performance. We evaluated the performance of DM-GCN on three well-known citation network datasets and the results showed that the proposed framework is more effective than several graph-based semi-supervised learning methods.

Near-Optimal Adversarial Reinforcement Learning with Switching Costs

Switching costs, which capture the costs for changing policies, are regarded as a critical metric in reinforcement learning (RL), in addition to the standard metric of losses (or rewards). However, existing studies on switching costs (with a coefficient $\beta$ that is strictly positive and is independent of $T$) have mainly focused on static RL, where the loss distribution is assumed to be fixed during the learning process, and thus practical scenarios where the loss distribution could be non-stationary or even adversarial are not considered. While adversarial RL better models this type of practical scenarios, an open problem remains: how to develop a provably efficient algorithm for adversarial RL with switching costs? This paper makes the first effort towards solving this problem. First, we provide a regret lower-bound that shows that the regret of any algorithm must be larger than $\tilde{\Omega}( ( H S A )^{1/3} T^{2/3} )$, where $T$, $S$, $A$ and $H$ are the number of episodes, states, actions and layers in each episode, respectively. Our lower bound indicates that, due to the fundamental challenge of switching costs in adversarial RL, the best achieved regret (whose dependency on $T$ is $\tilde{O}(\sqrt{T})$) in static RL with switching costs (as well as adversarial RL without switching costs) is no longer achievable. Moreover, we propose two novel switching-reduced algorithms with regrets that match our lower bound when the transition function is known, and match our lower bound within a small factor of $\tilde{O}( H^{1/3} )$ when the transition function is unknown. Our regret analysis demonstrates the near-optimal performance of them.

A Near-Optimal Algorithm for Safe Reinforcement Learning Under Instantaneous Hard Constraints

In many applications of Reinforcement Learning (RL), it is critically important that the algorithm performs safely, such that instantaneous hard constraints are satisfied at each step, and unsafe states and actions are avoided. However, existing algorithms for ''safe'' RL are often designed under constraints that either require expected cumulative costs to be bounded or assume all states are safe. Thus, such algorithms could violate instantaneous hard constraints and traverse unsafe states (and actions) in practice. Therefore, in this paper, we develop the first near-optimal safe RL algorithm for episodic Markov Decision Processes with unsafe states and actions under instantaneous hard constraints and the linear mixture model. It not only achieves a regret $\tilde{O}(\frac{d H^3 \sqrt{dK}}{\Delta_c})$ that tightly matches the state-of-the-art regret in the setting with only unsafe actions and nearly matches that in the unconstrained setting, but is also safe at each step, where $d$ is the feature-mapping dimension, $K$ is the number of episodes, $H$ is the number of steps in each episode, and $\Delta_c$ is a safety-related parameter. We also provide a lower bound $\tilde{\Omega}(\max\{dH \sqrt{K}, \frac{H}{\Delta_c^2}\})$, which indicates that the dependency on $\Delta_c$ is necessary. Further, both our algorithm design and regret analysis involve several novel ideas, which may be of independent interest.